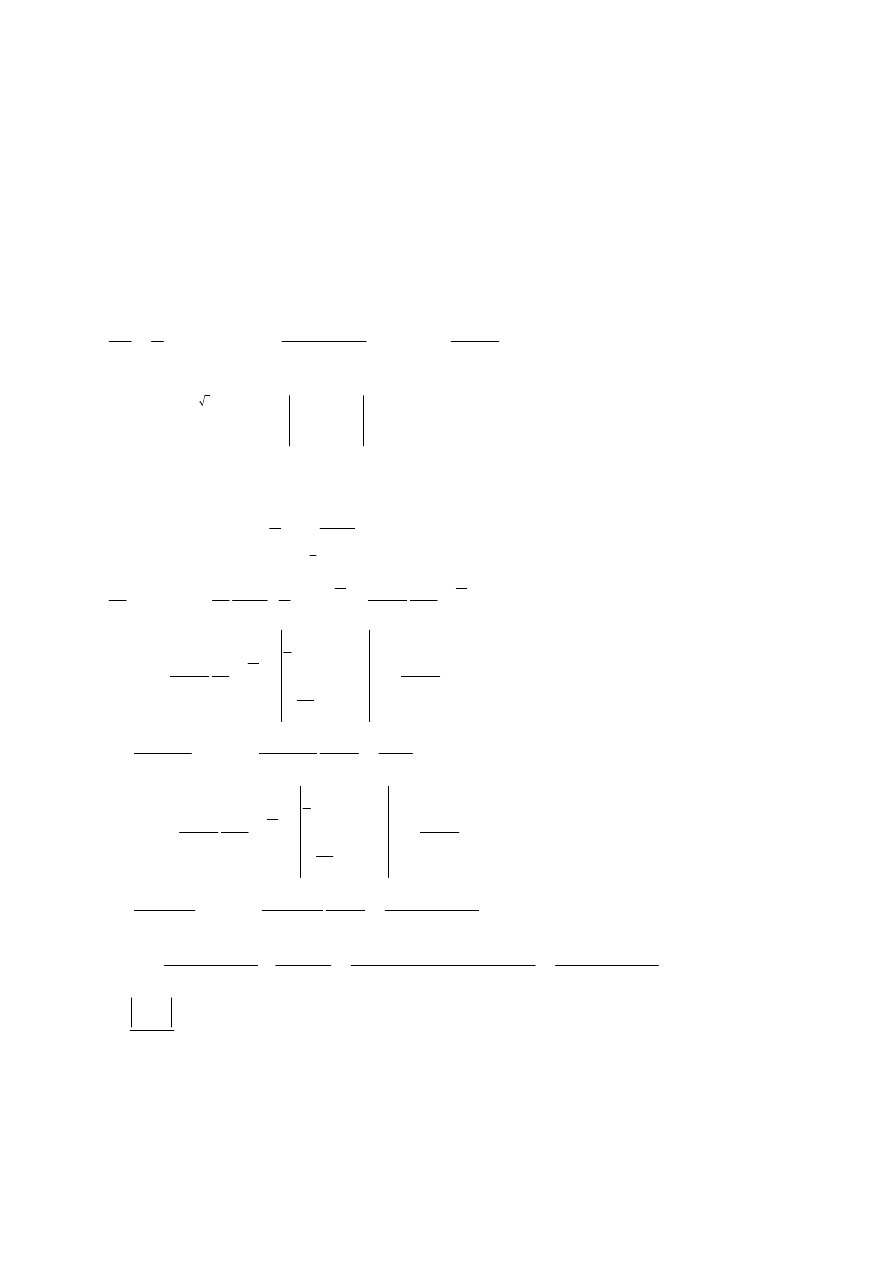
Egzamin dla Aktuariuszy z 4 października 2010 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
( )
( )
∏
=
−
∑
=
n
i
X
i
n
i
e
X
L
1
2
2
θ
θ
(
)
∑
∑
−
+
+
=
2
ln
ln
2
ln
ln
i
i
X
X
n
L
θ
θ
∑
∑
∑
=
=
→
=
−
→
=
−
=
∂
∂
n
i
i
i
i
X
n
X
n
X
n
1
2
2
2
ˆ
0
0
θ
θ
θ
θ
θ
(
)
∫
∫
≅
−
=
=
=
=
=
=
<
−
−
−
t
t
t
s
x
wykl
e
ds
e
ds
xdx
s
x
xe
t
X
P
0
0
2
2
)
(
1
2
2
2
θ
θ
θ
θ
θ
θ
( )
∑
=
Γ
≅
n
i
i
n
X
1
2
,
θ
( )
∫
∑
∞
−
−
Γ
=
>
=
<
t
n
x
n
n
i
dx
e
x
n
t
n
X
P
t
P
θ
θ
θ
1
2
)
(
ˆ
( )
(
)
( )
t
n
n
n
t
n
n
n
e
t
n
n
e
t
n
n
t
n
t
P
dt
d
θ
θ
θ
θ
θ
−
+
−
−
Γ
=
Γ
=
<
1
1
2
1
)
(
)
(
ˆ
( )
( )
( )
∫
∫
∞
∞
−
−
−
=
Γ
=
=
−
=
=
Γ
=
0
0
2
2
)
(
1
1
1
)
(
ˆ
nx
n
n
t
n
n
n
e
x
n
n
dx
dt
t
x
t
e
t
n
n
E
θ
θ
θ
θ
θ
( )
( )
( )
∫
∞
−
−
−
−
−
=
Γ
−
Γ
−
Γ
=
0
1
2
1
1
)
(
)
1
(
)
1
(
n
n
n
n
n
n
e
x
n
n
n
n
nx
n
n
θ
θ
θ
θ
θ
( )
( )
( )
∫
∫
∞
∞
−
−
−
−
=
Γ
=
=
−
=
=
Γ
=
0
0
3
2
1
2
)
(
1
1
1
)
(
ˆ
nx
n
n
t
n
n
n
e
x
n
n
dx
dt
t
x
t
e
t
n
n
E
θ
θ
θ
θ
θ
( )
( )
( )
∫
∞
−
−
−
−
−
−
=
Γ
−
Γ
−
Γ
=
0
2
2
2
3
2
)
1
)(
2
(
)
(
)
2
(
)
2
(
n
n
n
n
n
n
n
e
x
n
n
n
n
nx
n
n
θ
θ
θ
θ
θ
)
2
(
)
1
(
)
2
(
)
1
(
)
2
(
)
1
(
)
1
(
)
1
)(
2
(
ˆ
var
2
2
2
2
2
2
2
2
2
2
2
2
2
−
−
=
−
−
−
−
−
=
−
−
−
−
=
n
n
n
n
n
n
n
n
n
n
n
n
n
n
θ
θ
θ
θ
θ
θ
(
) (
)
=
≤
≤
=
<
−
≤
−
=
≤
−
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
01
,
1
ˆ
99
,
0
01
,
0
ˆ
01
,
0
01
,
0
ˆ
P
P
P

→
−
−
−
−
≤
≤
−
−
−
−
=
4
4 3
4
4 2
1
4
4 3
4
4 2
1
2
1
2
)
1
(
1
01
,
1
2
)
1
(
1
99
,
0
A
A
n
n
n
n
n
N
n
n
n
n
n
P
θ
θ
θ
θ
θ
θ
[
]
(
)
n
n
n
n
n
n
n
n
n
n
n
n
A
2
01
,
0
99
,
0
2
)
1
(
99
,
0
2
)
1
(
1
99
,
0
1
−
−
−
=
−
−
−
=
−
−
−
−
=
[
]
(
)
n
n
n
n
n
n
n
n
n
n
n
n
A
2
01
,
0
01
,
1
2
)
1
(
01
,
1
2
)
1
(
1
01
,
1
2
−
+
−
=
−
−
−
=
−
−
−
−
=
2
1
A
A
n
przy
≈
∞
→
To sprawdzimy:
(
)
→
=
→
=
−
→
=
−
<
38418
96
,
1
2
01
,
0
95
,
0
2
01
,
0
n
n
n
N
P
Sprawdzamy (E):
(
)
OK
P
→
−
→
95
,
1
;
96
,
1
Zadanie 2
{
}
(
) (
)
=
<
<
<
=
=
n
n
X
X
X
X
X
X
P
X
X
X
X
P
1
3
1
2
1
2
1
1
,...,
,
,...,
,
min
{
}
(
)
n
X
X
X
P
,...,
min
2
1
<
=
{
}
(
)
{
}
(
)
=
>
−
=
<
t
X
X
P
t
X
X
P
n
n
,..,
min
1
,...,
min
2
2
(
)
∏
=
−
+
−
−
→
−
=
∑
−
=
>
−
=
=
n
i
t
n
n
i
t
i
e
e
t
X
P
n
i
2
2
)
1
)(
2
(
1
1
1
2
−
+
≅
≅
<
=
→
2
)
1
)(
2
(
),
1
(
gdzie
)
(
n
n
wykl
Y
wykl
X
Y
X
P
ODP
∫ ∫
∞
−
+
−
−
=
−
+
=
0 0
2
)
1
)(
2
(
2
)
1
)(
2
(
y
y
n
n
x
dxdy
e
n
n
e
ODP
(
)
∫
∞
−
=
+
−
+
−
+
−
=
−
−
+
−
−
+
=
0
1
2
)
1
)(
2
(
2
)
1
)(
2
(
1
1
2
)
1
)(
2
(
exp
2
)
1
)(
2
(
n
n
n
n
dy
e
y
n
n
n
n
y
n
n
n
n
n
n
n
n
n
n
n
n
+
=
+
−
+
−
+
−
+
−
+
=
+
−
+
−
+
−
=
2
2
2
)
1
)(
2
(
)
1
)(
2
(
2
)
1
)(
2
(
2
)
1
)(
2
(
)
1
)(
2
(
1
Zadanie 3
1
2
θ
θ
>

(
)
( )
(
)
(
)
( )
(
)
=
+
+
+
+
=
∏
∏
∏
∏
=
+
=
+
=
+
=
+
5
1
1
2
5
1
10
1
1
10
1
5
1
1
2
5
2
10
1
1
1
10
2
1
1
2
2
1
2
1
1
2
1
i
i
i
i
i
i
i
y
x
y
x
P
θ
θ
θ
θ
θ
θ
θ
θ
(
)
(
)
(
)
∏
∏
=
=
−
−
→
+
+
⋅
⋅
=
10
1
5
1
2
5
15
1
5
15
2
2
1
2
1
1
1
2
2
i
i
i
i
y
x
θ
θ
θ
θ
θ
θ
→
jest rosnąca funkcją statystyki
(
) (
)
∏
∏
=
=
+
+
10
1
5
1
2
1
1
1
i
i
i
i
y
x
05
,
0
)
(
=
>
c
STAT
P
(
)
(
)
(
)
(
)
∫
−
+
+
=
−
<
=
<
+
1
0
1
1
1
1
ln
t
e
i
t
i
i
x
e
X
P
t
x
P
θ
θ
(
)
)
(
)
(
)
1
(
1
ln
θ
θ
θ
θ
θ
wykl
e
e
e
t
f
t
t
t
x
i
≅
=
=
−
+
+
(
)
(
)
(
)
∫
−
+
+
=
<
+
1
0
1
2
2
1
2
1
ln
2
t
e
i
i
y
t
y
P
θ
θ
(
)
)
(
2
1
2
)
(
2
)
1
2
(
2
1
ln
2
θ
θ
θ
θ
θ
wykl
e
e
e
t
f
t
t
t
y
i
≅
=
=
−
+
+
(
)
(
)
(
)
(
)
∑
∑
∑
∑
=
=
=
=
Γ
≅
+
+
+
→
Γ
≅
+
Γ
≅
+
10
1
5
1
10
1
5
1
)
;
15
(
1
ln
1
ln
)
;
5
(
1
ln
),
;
10
(
1
ln
i
i
i
i
i
i
i
i
Y
X
Y
X
θ
θ
θ
(
)
)
,
15
(
gdzie
ln
1
1
)
(
θ
Γ
≅
−
<
=
<
=
>
X
t
X
P
t
STAT
P
t
STAT
P
Szukamy takiego t, że: P(X<t)=0,05 i
)
1
;
15
(
Γ
≅
X
∫
∫
=
Γ
=
=
=
Γ
−
−
t
t
s
x
ds
e
s
s
x
dx
e
x
0
2
0
2
14
15
14
05
,
0
)
15
(
2
1
2
)
15
(
1
to jest całka z gęstości rozkładu
)
30
(
2
χ
Z tablic 2t=18,493 czyli t=9,2465 czyli około 9,25
Zadanie 4
Dla rozkładu złożonego ujemnego dwumianowego:
+
+
=
3
2
2
2
3
,
3
)
(
2
)
(
3
EX
p
q
EX
EX
p
q
EX
p
q
r
N
S
µ
+
=
2
2
)
(
var
EX
p
q
EX
p
q
r
S
N
≅
4
1
;
1
.dwumianowy
uj
N

(
)
27
47
9
2
2
3
3
1
1
75
,
0
25
,
0
2
2
1
75
,
0
25
,
0
3
3
75
,
0
25
,
0
3
2
2
3
=
+
+
=
⋅
⋅
+
⋅
⋅
⋅
+
=
−
N
ES
S
E
N
9
7
3
1
2
3
1
1
75
,
0
25
,
0
2
75
,
0
25
,
0
var
2
=
+
=
⋅
+
=
N
S
538
,
2
7
7
47
7
7
27
27
47
9
7
27
47
2
3
≈
=
=
=
ODP
Zadanie 5
Dla pierwszych 200 osób:
(
)
3
1
3
1
6
2
)
1
(
6
4
1
+
=
−
+
⋅
=
=
q
q
q
Z
P
i
(
)
q
Z
P
i
3
1
3
2
0
−
=
=
Dla pozostałych 200 osób:
(
)
q
q
q
Z
P
i
3
1
3
2
6
4
)
1
(
6
2
1
−
=
−
+
=
=
(
)
q
Z
P
i
3
1
3
1
0
+
=
=
2
2
1
1
200
200
200
200
200
200
3
1
3
1
3
1
3
2
3
1
3
2
3
1
3
1
Z
Z
Z
Z
q
q
q
q
L
−
−
+
−
−
+
=
(
)
(
)
+
−
+
−
+
−
−
+
+
=
q
Z
q
Z
q
Z
q
Z
L
3
1
3
1
ln
200
200
3
1
3
2
ln
200
3
1
3
2
ln
200
200
3
1
3
1
ln
200
ln
2
2
1
1
(
)
(
)
0
3
1
3
1
3
1
200
200
3
1
3
1
3
2
200
3
1
3
1
3
2
200
200
3
1
3
1
3
1
200
2
2
2
1
=
+
−
+
−
−
−
−
−
+
=
∂
∂
q
Z
q
Z
q
Z
q
Z
q
(
)
(
)
(
)
→
=
−
+
−
−
+
+
−
+
−
−
−
0
)
2
)(
1
(
)
2
(
1
)
1
(
)
1
(
1
2
2
2
1
1
q
q
q
Z
q
Z
q
Z
q
Z
(
)
2
1
2
2
1
1
2
2
1
1
2
3
2
3
2
1
2
2
1
2
1
1
Z
Z
q
Z
Z
Z
Z
Z
Z
Z
Z
q
−
+
=
→
+
−
+
−
+
−
=
+
−
−
+
−
−
→
Zadanie 6
(
)
(
)
∑
∑
∑
=
≠
=
=
+
=
n
i
j
i
j
j
i
i
i
i
n
i
i
i
X
X
X
X
1
1
,
cov
var
var
ε
ε
ε
ε
(
)
(
)
j
j
i
i
i
i
X
X
n
n
X
n
ε
ε
ε
,
cov
)
1
(
var
−
+
=
(
) ( ) ( )
µ
µ
ε
ε
2
1
2
1
3
1
3
1
=
+
=
=
i
i
i
i
X
E
E
X
E
(
)
(
)
(
)
2
2
2
2
2
2
12
5
3
1
4
1
3
1
µ
δ
δ
µ
ε
+
=
+
+
=
i
i
X
E
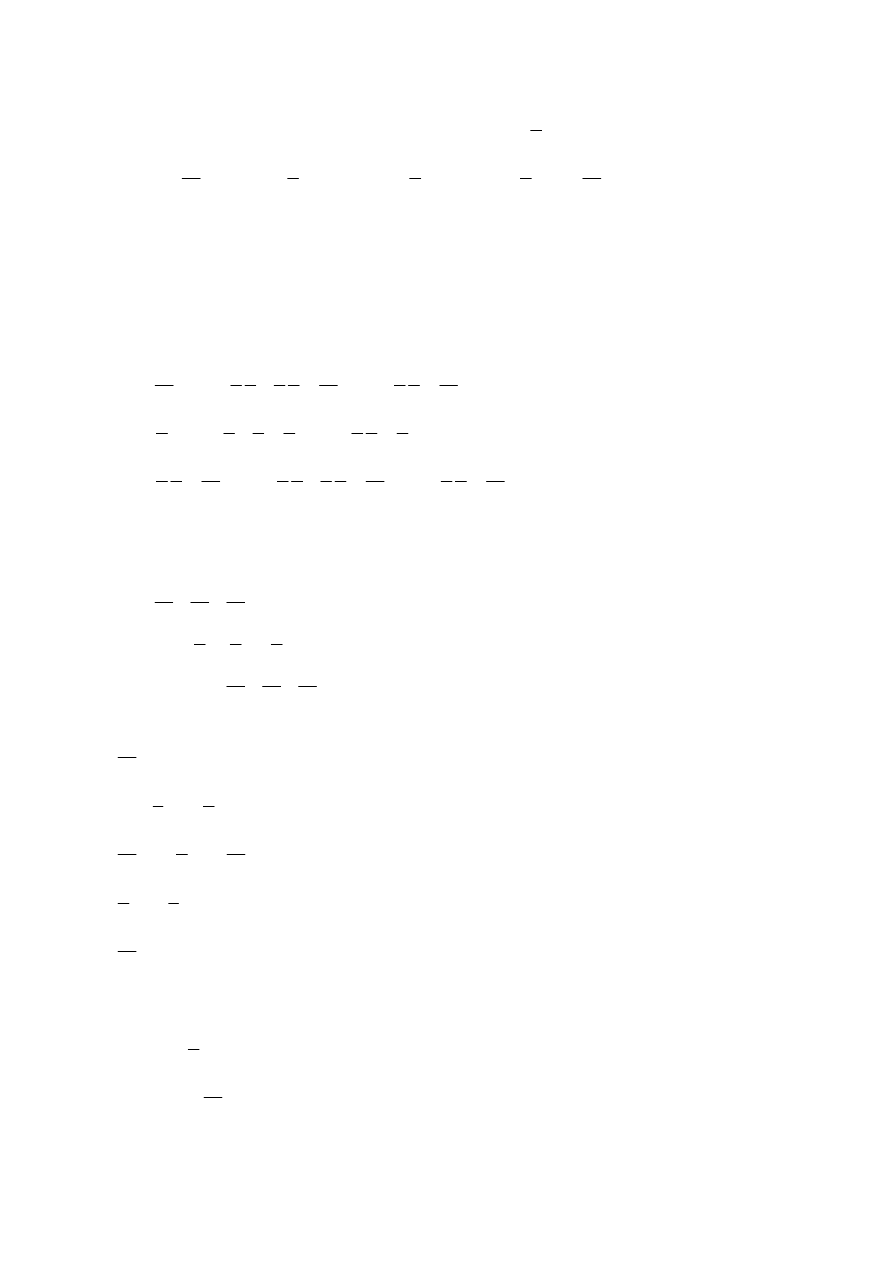
(
)
( )
( ) (
)
( ) ( )
[
] [
]
2
2
4
1
,
cov
,
µ
δ
ε
ε
ε
ε
+
=
+
=
p
X
E
X
E
X
X
E
E
X
X
E
j
i
j
i
j
i
j
j
i
i
(
)
(
)
[
]
2
2
2
2
2
2
2
2
2
)
1
(
3
2
5
12
4
1
4
1
)
1
(
4
1
12
5
var
δ
µ
δ
µ
µ
δ
µ
µ
δ
p
n
n
p
n
n
n
S
−
+
+
=
−
+
−
+
−
+
=
Zadanie 7
Przez stan oznaczamy ilość kul białych w I urnie:
)
1
(
)
(
−
→
i
i
STAN
białych
1
16
1
4
1
4
1
,
16
6
4
1
4
3
4
1
4
3
,
16
9
4
3
4
3
4
1
2
1
2
1
,
2
1
4
1
4
1
,
4
1
16
9
4
3
4
3
,
16
6
4
1
4
3
4
3
4
1
,
16
1
1
4
,
5
5
,
4
4
,
4
3
,
4
4
,
3
3
,
3
2
,
3
3
,
2
2
,
2
1
,
2
2
,
1
=
=
=
=
+
=
=
=
=
=
=
+
=
=
=
=
=
+
=
=
=
p
p
p
p
p
p
p
p
p
p
p
=
0
1
16
1
16
6
0
16
9
0
0
0
0
0
4
1
2
1
4
1
0
0
0
16
9
16
6
16
1
0
0
0
1
0
M
szukamy rozkładu stacjonarnego:
=
=
+
=
+
+
=
+
+
=
5
4
4
4
3
3
4
3
2
2
3
2
1
1
2
16
1
8
3
4
1
16
9
2
1
16
9
4
1
8
3
16
1
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
1
4
1
4
1
1
1
3
1
3
1
1
1
2
16
36
16
9
18
9
36
16
4
1
6
16
p
p
p
p
p
p
p
p
p
p
p
p
p
p
=
→
=
+
+
=
→
=
+
+
=

1
5
p
p
=
Ale
70
1
1
16
36
16
1
1
1
1
1
1
1
5
4
3
2
1
=
→
=
+
+
+
+
→
=
+
+
+
+
p
p
p
p
p
p
p
p
p
p
p
70
1
,
70
16
,
70
36
,
70
16
5
4
3
2
=
=
=
=
p
p
p
p
A – zdarzenie, że wylosowane kule są jednakowego koloru
(
)
(
)
=
+
+
+
+
+
=
=
∑
=
∞
→
4
3
4
1
4
1
4
3
4
1
4
1
4
1
4
3
4
3
4
1
)
(
)
(
lim
4
3
2
5
1
p
p
p
i
STAN
P
i
STAN
A
P
ODP
i
n
7
3
35
15
35
3
35
9
35
3
8
3
70
16
70
36
2
1
70
16
8
3
=
=
+
+
=
+
+
=
Zadanie 8
(
)
∑
=
=
−
−
n
i
i
a
x
b
n
e
b
L
1
ban
n
X
b
b
n
L
+
−
=
ln
ln
Szukamy max:
ab
X
b
b
b
a
f
+
−
=
ln
)
,
(
0
0
=
→
=
=
∂
∂
b
bn
a
czyli szukamy w inny sposób
Przy ustalonym b: max jest dla maksymalnego a czyli
( )
i
X
a
min
=
Max b szukamy licząc pochodną:
n
b
n
a
n
x
X
T
X
T
x
X
b
a
X
b
,
1
,
1
:
1
1
,
1
0
1
−
=
=
→
−
=
→
=
+
−
bn
a
EX
n
1
,
1
+
=
to łatwo policzyć
Skorzystamy z własności rozkładu wykładniczego z parametrem
λ
(brak pamięci, łatwo
pokazać):
(
)
(
)
)......
2
(
),
1
(
,
,
2
,
3
,
1
,
2
,
1
−
−
−
−
n
X
X
n
X
X
nX
n
n
n
n
n
są niezależne i mają rozkład
)
(
λ
wykl
Oznaczamy:
(
)
∑
∑
∑
=
=
=
−
=
−
−
+
=
−
=
−
n
i
n
i
n
i
n
n
i
n
i
n
n
i
n
nY
Y
n
na
nY
a
Y
n
nX
X
n
X
X
2
,
1
2
,
1
,
2
,
1
,
,
1
1
gdzie
i
Y mają rozkład wykładniczy już bez przesunięcia
(
)
(
)
n
n
n
n
n
n
n
i
n
n
i
Y
Y
n
Y
Y
n
nY
Y
:
1
:
:
1
:
2
2
,
1
,
...
)
1
(
1
−
=
−
+
+
−
−
=
−
∑
)
,
1
(
gdzie
0
b
n
X
X
n
E
ET
−
Γ
≅
=
→
∫
∞
−
−
−
−
−
−
=
−
Γ
−
Γ
=
−
Γ
=
0
2
1
2
1
2
)
2
(
)
1
(
)
1
(
b
n
n
b
n
n
b
n
e
x
n
b
x
n
ET
n
n
bx
n
n
b

Zadanie 9
(
)
(
)
∫
∞
+
−
−
=
=
=
=
−
=
Π
=
>
>
e
t
x
x
e
dt
dx
x
t
x
dx
e
e
X
P
e
X
X
E
1
8
1
ln
1
1
ln
2
2
1
)
(
2
∫
∫
∞
∞
−
−
+
−
≅
>
=
Π
=
Π
=
0
0
3
2
8
)
4
(
1
8
)
4
,
4
(
gdzie
)
0
(
2
2
1
2
2
1
2
2
N
Y
Y
P
e
e
e
e
dt
e
e
t
t
t
(
)
)
1
,
0
(
gdzie
)
2
(
)
(
3
N
N
N
P
e
e
X
P
e
X
X
E
≅
−
>
=
>
>
→
(
)
∫
∫
∞
∞
−
−
−
=
Π
=
Π
⋅
=
>
e
t
x
dt
e
dx
e
x
e
X
P
0
8
8
1
ln
2
1
2
2
1
2
2
1
)
(
2
2
(
) (
) (
)
(
)
=
+
>
>
>
=
+
>
=
>
+
=
>
EY
e
X
P
e
X
P
e
X
X
E
EY
e
X
X
E
e
X
Y
X
E
e
X
S
E
)
(
)
(
26
,
41
2
97725
,
0
2
tablic
z
2
)
2
(
2
3
3
≈
+
⋅
≅
=
+
−
>
=
e
N
P
e
Zadanie 10
(
) (
)
(
)
( )
∫
+
−
−
−
+
−
−
−
≅
→
−
=
−
=
=
+
<
≤
=
=
1
)
1
(
1
1
k
k
i
k
k
k
x
i
i
e
geom
Y
e
e
e
e
e
k
X
k
P
k
Y
P
λ
λ
λ
λ
λ
λ
λ
(
)
(
)
∏
=
+
−
−
−
=
5
1
1
i
Y
Y
i
i
e
e
L
λ
λ
(
)
(
)
(
)
(
)
(
)
∑
∑
∑
=
=
=
−
−
+
−
−
−
+
−
=
−
+
−
=
−
=
5
1
5
1
5
1
1
1
ln
5
1
ln
ln
ln
i
i
i
i
i
Y
Y
e
Y
e
Y
e
e
L
i
i
λ
λ
λ
λ
λ
λ
(
)
∑
∑
∑
=
=
=
−
−
+
=
→
=
−
−
−
→
=
−
+
−
=
∂
∂
5
1
5
1
5
1
1
5
ln
ˆ
0
1
5
1
0
1
5
ln
i
i
i
i
i
i
Y
e
Y
e
e
e
Y
L
λ
λ
λ
λ
λ
λ
(
)
∑
=
−
≅
=
5
1
,
5
.
i
i
e
dwum
uj
Y
Y
λ
(
) (
)
(
)
=
−
<
=
<
−
=
>
+
=
>
+
=
>
+
4
3
42
1
002
,
1
79
,
1
79
,
1
79
,
1
79
,
1
1
5
5
1
5
1
5
79
,
1
1
5
ln
e
Y
P
Y
e
P
Ye
Y
P
e
Y
P
Y
P
(
)
(
)
(
) (
)
286
,
0
5
1
1
1
1
5
1
0
4
)
1
(
)
0
(
1
5
1
1
5
1
5
1
0
≈
+
−
=
−
+
−
=
=
+
=
=
−
−
−
−
−
e
e
e
e
e
Y
P
Y
P
H
Wyszukiwarka
Podobne podstrony:
2010.10.04 prawdopodobie stwo i statystyka
2004 10 11 prawdopodobie stwo i statystykaid 25166
1998 10 03 prawdopodobie stwo i statystykaid 18585
2002 10 12 prawdopodobie stwo i statystykaid 21648
2010 12 13 prawdopodobie stwo i statystykaid 27016
2011 04 04 prawdopodobie stwo i statystykaid 27339
1996 10 26 prawdopodobie stwo i statystykaid 18572
2001.10.13 prawdopodobie stwo i statystyka
2008.10.06 prawdopodobie stwo i statystyka
2007.10.08 prawdopodobie stwo i statystyka
2006.10.09 prawdopodobie stwo i statystyka
2004.10.11 prawdopodobie stwo i statystyka
2009.10.05 prawdopodobie stwo i statystyka
1999 10 23 prawdopodobie stwo i statystykaid 18598
2009 10 05 prawdopodobie stwo i statystykaid 26670
2000.10.14 prawdopodobie stwo i statystyka
1996.10.26 prawdopodobie stwo i statystyka
2003.10.11 prawdopodobie stwo i statystyka
2010.05.31 prawdopodobie stwo i statystyka
więcej podobnych podstron