Vol. 30 no. 4 2014, pages 497–505

BIOINFORMATICS

ORIGINAL PAPER

doi:10.1093/bioinformatics/btt716

Structural bioinformatics

Advance Access publication December 12, 2013

Sequence-based Gaussian network model for protein dynamics

Hua Zhang

1,

* and Lukasz Kurgan

2

1

School of Computer and Information Engineering, Zhejiang Gongshang University, Hangzhou, Zhejiang 310018, P.R.

China and

2

Department of Electrical and Computer Engineering, University of Alberta, Edmonton, Alberta T6G 2V4,

Canada

Associate Editor: Anna Tramontano

ABSTRACT

Motivation: Gaussian network model (GNM) is widely adopted to ana-
lyze and understand protein dynamics, function and conformational
changes. The existing GNM-based approaches require atomic coord-
inates of the corresponding protein and cannot be used when only the
sequence is known.
Results: We report, first of its kind, GNM model that allows modeling
using the sequence. Our linear regression-based, parameter-free, se-
quence-derived GNM (L-pfSeqGNM) uses contact maps predicted
from the sequence and models local, in the sequence, contact neigh-
borhoods with the linear regression. Empirical benchmarking shows
relatively high correlations between the native and the predicted with
L-pfSeqGNM B-factors and between the cross-correlations of residue
fluctuations derived from the structure- and the sequence-based
GNM models. Our results demonstrate that L-pfSeqGNM is an attract-
ive platform to explore protein dynamics. In contrast to the highly
used GNMs that require protein structures that number in thou-
sands, our model can be used to study motions for the millions of
the readily available sequences, which finds applications in modeling
conformational changes, protein–protein interactions and protein
functions.
Contact: [e-mail]
Supplementary information: Supplementary data are available at
Bioinformatics online.

Received on July 29, 2013; revised on November 16, 2013; accepted
on December 7, 2013

1

INTRODUCTION

Protein dynamics, which is associated with ever-present thermal
fluctuations of atoms and other types of motions that span
between rapid (picoseconds) vibrations and relatively slow
(microseconds to seconds) movements (Atilgan et al., 2001), im-
plements various important biological processes and functions
(Bakan and Bahar, 2009; Bahar and Rader, 2005). The X-ray
crystallography studies provide information about the thermal
motion, which is represented by the Debye–Waller temperature
factors or B-factors. B-factors are proportional to the mean
square fluctuations of atomic positions in a crystal due to the
thermal motion and positional disorder. They have been studied
from a variety of viewpoints in the context of protein function
(Bhalla et al., 2006; Jiang et al., 2011) and their relation with
conformational

changes

on

protein–protein

interactions

(Dobbins et al., 2008; Eisenmesser et al., 2005), to name just a

few. Consequently, the knowledge of B-factors provides import-
ant insights into the functional dynamics of proteins.

Several computational and physical models have been pro-

posed to predict the B-factors from protein structures (Erman,
2006; Halle, 2002), electron density maps (Ming et al., 2002) and
sequences (Schlessinger and Rost, 2005; Yuan et al., 2005; Zhang
et al.

, 2009). To overcome the high computational cost of mo-

lecular dynamic simulations (Rueda et al., 2007), several struc-
ture-based computational approaches, such as the coarse-grained
models including normal mode analysis (Bahar and Rader,
2005), elastic network model (ENM) (Yang et al., 2007a), pack-
ing density (Halle, 2002) and weighted contact number (Lin
et al.

, 2008) were developed. The ENMs, including the isotropic

Gaussian network model (GNM) (Bahar et al., 1997; Kundu
et al.

, 2002) and the anisotropic network model (Atilgan et al.,

2001), define spring-like interactions between residues that are
within a certain cutoff distance. They simplify the computation-
ally costly all-atom potentials into a quadratic function in the
vicinity of the native state, which allows the decomposition of the
motions into vibrational modes with different frequencies, which
are known as normal modes. They can determine the (concerted)
collective motions of residues that correspond to the lowest-fre-
quency modes comprising large parts of a given protein (Bahar
et al.

, 1999). Being simple and efficient, ENM and GNM have

been widely applied to study many motion problems, such as the
molecular mechanisms of the GroEL-GroES function (Keskin
et al.

, 2002), motor-protein motions (Zheng and Doniach,

2003) and general conformational changes and functions
(Bakan and Bahar,

2009;

Haliloglu and Erman, 2009;

Haliloglu et al., 2008; Jiang et al., 2011; Kurkcuoglu and
Bates, 2010; Marcos et al., 2011; Srivastava and Granek, 2013;
Szarecka et al., 2007; Tuzmen and Erman, 2011; Wieninger et al.,
2011; Yang and Bahar, 2005; Yang et al., 2007b; Yang et al.,
2008; Zheng and Brooks, 2005; Zhu and Hummer, 2010;
Zhuravleva et al., 2007). Moreover, several variations of the clas-
sical ENMs (i.e.the classical GNMs and anisotropic network
models) (Atilgan et al., 2001; Kundu et al., 2002) have been de-
veloped for better modeling of protein dynamics (Erman, 2006;
Kim et al., 2011; Mendez and Bastolla, 2010; Song and Jernigan,
2007; Yang et al., 2009; Zheng, 2008, 2010). However, these
methods require the knowledge of protein structure, which
limits their applications to thousands of known structures, in
contrast to the millions of known non-redundant protein
sequences.

The sequence-based predictors use only the protein sequences

as their input and thus, they are suitable for the analysis of the

*To whom correspondence should be addressed.

ß The Author 2013. Published by Oxford University Press.

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/), which permits

non-commercial re-use, distribution, and reproduction in any medium, provided the original work is properly cited. For commercial re-use, please contact [e-mail]

at Uniwertytet Gdanski on May 28, 2014

http://bioinformatics.oxfordjournals.org/

Downloaded from

chains with unknown structures. Yuan et al. (2005) applied sup-
port vector regression to predict the B-factors using position-
specific scoring matrix generated from the input sequence.
Schlessinger and Rost (2005) proposed a neural network model
that uses evolutionary information and solvent accessibility that
are generated and predicted from the input chain, respectively.
Zhang et al. (2009) used the linear regression to investigate the
local impact of solvent accessibility on the residue flexibility.
Recently, Hirose et al. (2010) developed a random forest-based
model that uses the input sequence and the predicted secondary
structure and solvent accessibility, and Bornot et al. (2011) used
a sequence fragment matching-based approach to model the pro-
tein flexibility. Nevertheless, the main drawback of these se-
quence-based predictors is that they predict only the B-factor
values of the C atoms, and they do not provide the information
about the collective motions.

Motivated by recent advances in high-throughput sequencing

and lagging of the current structure determination pipelines, a
sequence-based model would be invaluable to advance our
understanding of protein motion and flexibility. We address
this need

by proposing a

novel

sequence-based

GNM

(SeqGNM) that uses contact maps predicted from the sequences
with the NNcon method (Tegge et al., 2009). Furthermore,
inspired by a finding that strength of the relation between solvent
accessibility and flexibility of residues improves when considering
a local neighborhood in the sequence (Zhang et al., 2009) and the
development of the local contact density model (Halle, 2002), we
enhance SeqGNM by using a linear regression that quantifies
relation between the local predicted contacts and the flexibility.
We illustrate the benefits of the SeqGNM by applying it to pre-
dict B-factors and collective motions of residues. We demon-
strate that results from SeqGNM are comparable with the
outputs from the structure-based GNMs.

2

METHODS

2.1

Datasets and input data

We use a benchmark dataset that was developed in Yang et al. (2009) and
filtered using Protein Data Bank (PDB)-REPRDB (Noguchi and
Akiyama, 2003). It includes 972 protein chains extracted from the PDB
(Berman et al., 2000) that have length 60, pairwise sequence identity

25% and high-quality (resolution 2.0 A˚ and R-factor 0.2) X-ray

structures (to derive reliable values of the native B-factors). Similarly,
as in Zhang et al. (2009), the average correlation coefficient (ACC) was
used to evaluate the performance of various models.

We use NNcon (Tegge et al., 2009) to predict contact maps from

protein chains, which are used as inputs to derive the SeqGNM.
Prediction of protein contact map is an active research topic, and a
number of residue–residue contact predictors have been developed
including SVMcon (Cheng and Baldi, 2007), NNcon (Tegge et al.,
2009), ProC_S3 (Li et al., 2011), DNCON (Eickholt and Cheng, 2012),
CMAPpro (Di Lena et al., 2012), CNNcon (Ding et al., 2013),
PhyCMAP (Wang and Xu, 2013) and so forth. We selected NNcon be-
cause only this method has a standalone version that can be used for
large-scale predictions and provides contact predictions for all residue
pairs in the input sequence; other predictors have no standalone versions
or output only a part of the inter-residue contact predictions, such as the
top L or L/2 predictions. The NNcon method limits the maximum size of
the input chain to 800 residues, and consequently, 21 chains from the

benchmark dataset that were longer than 800 were removed. The final
dataset includes 951 proteins and is named as PDB951.

We also prepared another independent (dissimilar to the proteins that

were used to build NNcon and in the PDB951 dataset that is used to
design models) dataset. This dataset includes sequences that were solved
by X-ray crystallography and that were deposited in PDB between
January 2012 and September 2013, i.e. after PDB951 dataset was col-
lected and after the NNcon method was released. Next, NCBI’s
BLASTCLUST (Altschul et al., 1997) with the local identity threshold
at 25% (S 25) was applied to the union of this set, the PDB951 dataset
and the training dataset used to develop NNcon. The independent dataset
was constructed by selecting one chain with length between 60 and 800
residues, resolution 2.0 A˚ and R-factor 0.2 from each cluster that
contains no sequences from the PDB951 dataset and the training set
used in the NNcon method. Consequently, this dataset, called PDB748,
includes 748 chains that have local identity of at most 25% with each
other and also with the protein chains from the PDB951 dataset and the
NNcon’s training dataset. When testing on the PDB748 dataset, our
model is built using proteins from the PDB951 dataset. The PDB IDs
of chains included in the PDB951 and PDB748 datasets are provided in
the Supplementary Tables S2 and S3, respectively.

2.2

Calculation of normalized B-factors

Experimental B-factor of an atom is defined as 8

2

5u

2

4 using the iso-

tropic mean square displacement, u

2

, averaged over the lattice. As the

B-factor values depend on the experimental resolution, crystal contacts
and the refinement procedures, they are normalized between structures.
Following (Schlessinger and Rost, 2005; Zhang et al., 2009), the B-factors
of the C

atoms (C

atoms for Gly) for each chain were normalized as

B

’¼(B-AVE)/, where B is the native B-factor, AVE is the average native

B-factor in a given chain and is the standard deviation of native
B-factors for all C

atoms (C

atoms for Gly) in a given chain.

2.3

Gaussian network model and parameter-free GNM

Each protein in GNM is modeled by an elastic network, where the
springs connecting the nodes represent the bonded and non-bonded inter-
actions between the pairs of residues located within a cutoff distance R

C

(Kundu et al., 2002). Assuming that the fluctuations between residues are
isotropic and Gaussian, the potential of the network of N nodes (resi-
dues) is

V

GNM

¼

2

X

N

i

, j

ij

ð

R

ij

R

0
ij

Þ

2

ð

1Þ

where R

ij

and R

0

ij

are instantaneous and original distance vectors between

residues i and j, respectively, is the force constant that is assumed to be
uniform for all network springs and ¼ (

ij

) is the following Kirchhoff

matrix based on the contact information:

ij

¼

1,

if i 6¼ j and R

0

ij

R

C

0,

if i 6¼ j and R

0

ij

R

C

P

j

:j6¼i

ij

, if i ¼ j

8

>

>

<

>

>

:

ð

2Þ

where R

0

ij

is the distance between residues i and j. Then, the mean square

fluctuation of the ith residue is given by

5R

2
i

4 ¼ ð3k

B

T=Þ½

1

ii

ð

3Þ

where k

B

is the Boltzmann constant, T is temperature and is a constant

scaling factor. The cross-correlation map, which includes the mean cor-
relations between residue fluctuations, is given by

5R

i

R

j

4 ¼ ð3k

B

T=Þ½

1

ij

ð

4Þ

498

H.Zhang and L.Kurgan

at Uniwertytet Gdanski on May 28, 2014

http://bioinformatics.oxfordjournals.org/

Downloaded from

Furthermore, Yang et al. (2009) proposed parameter-free GNM

(pfGNM) that replaces the cutoff distance R

C

by introducing a more

physical concept of inverse power dependence for the residue–residue
interactions. In pfGNM, the elements of the Kirchhoff matrix are calcu-
lated as

pf
ij

¼

R

2

ij

if i 6¼ j

P

j

:j6¼i

pf
ij

if i ¼ j

8

<

:

ð

5Þ

where R

ij

is the distance between residues i and j.

2.4

Sequence–based Gaussian network models

In this work, the GNM is calculated from the sequence-predicted contact
maps that are generated with the NNcon method (Tegge et al., 2009).
NNcon provides probability values P

ij

2

[0, 1] that express the strength of

the contact between C

atoms (C

atoms for Gly) of residues i and j.

Similar to the classical GNM and the pfGNM, the corresponding two
types of the SeqGNMs are proposed. One is based on the probability
cutoff P

C

and the other directly uses the probability values to construct

the Kirchhoff matrix. The Kirchhoff matrix of the classical SeqGNM is
defined as

Seq
ij

¼

1,

if i 6¼ j and P

ij

P

C

0,

if i 6¼ j and P

ij

P

C

P

j

:j6¼i

Seq
ij

,

if i ¼ j

8

>

<

>

:

ð

6Þ

and the Kirchhoff matrix of the parameter-free sequence-based pfGNM
(pfSeqGNM) is defined as

pfSeq

ij

¼

P

ij

,

if i 6¼ j

P

j

:j6¼i

pfSeq

ij

, if i ¼ j

(

ð

7Þ

2.5

Linear regression models

As shown in Erman (2006), the Kirchhoff matrix in GNM could be
written as ¼ D þ U, where D and U are the matrices of the diagonal
and off-diagonal elements, respectively. Furthermore, the inverse

1

¼

(D þ U)

1

could be written in the form of Taylor series expansion:

1

¼

D

1

– D

1

U D

1

þ

. . . As a result, the diagonal component D

1

quantifies the main contribution of the local packing density to

1

. The

second term, D

1

U D

1

, provides a relatively weak contribution resulting

from the positional correlations among different residue pairs. Moreover,
Halle (2002) proposed the local density model, where only the contribu-
tions of diagonal terms are considered. Based on their findings (Erman,
2006; Halle, 2002), we use a linear regression model to investigate the
local impact of the diagonal terms of

pfSeq

on the performance of

B-factor prediction. The flexibility of the ith residue, which is located at
the center of a window that defines local neighborhood, denoted as
B’-factor, is defined as

^

B

0
i

¼

X

h

k¼h

w

k

pfSeq
iþk

, iþk

þ

b

ð

8Þ

where b is the intercept, weighs w

k

are determined using the least squares

fit between the estimated and the native B’-factor values and the window
includes 2 hþ1 residues, where h ¼ 0,1,2, . . . . This linear model is empir-
ically shown to improve the B’-factor prediction when compared with the
case in which only the diagonal terms are used. Furthermore, the w

k

weighs learned from the PDB951 dataset with optimal window size h
are used to construct a new Kirchhoff matrix, which is empirically
shown to improve the B’-factor predictions when compared with the
GNM that does not use this extension (see Section 3). This extended
model also allows the calculation of the cross-correlations of the residue

fluctuations. The Linear regression-based, parameter-free, Sequence-
derived GNM (L-pfSeqGNM) is defined as

L

-

pfSeq

ij

¼

P

h

k¼h

w

k

pfSeq

iþk

, jþk

,

if i 6¼ j

P

j

:j6¼i

LpfSeq

ij

,

if i ¼ j

8

>

>

<

>

>

:

ð

9Þ

where

pfSeq

iþk

, jþk

¼

0 when i þ k 0, j þ k 0 or i þ k N þ 1, j þ k

N þ

1 and N is the length of the protein chain.

3

RESULTS

3.1

Impact of the contact prediction probability cutoffs on
the prediction of residue flexibility with SeqGNM

The NNcon method, which generates inputs for SeqGNM, pro-
vides predicted probability values for the residue–residue contacts.
Motivated by the assessments of the residue–residue contact pre-
dictions in Critical Assessment of Protein Structure Prediction
(CASP) (Monastyrskyy et al., 2011), NNcon (Tegge et al., 2009)
defines contacts between C

(C

for Gly) atoms using two thresh-

olds at 8 and 12 A˚; other thresholds are not considered. We use the
classical GNM that applies binary contacts, where the contact
probabilities are binarized using varying cutoffs that are shown
on the x-axis in Figure 1. The ACC values between the predicted
and the native B’-factors (shown on the y-axis in Fig. 1) are higher
when defining the contacts at 12 A˚, and thus, we select this defin-
ition throughout all subsequent results. Binarization of the prob-
abilities predicted by NNcon with cutoff at 0.3, i.e. a given pair of
residues is in contact when the probability40.3, leads to ACC
value equals 0.456, which indicates relatively good correlation.

3.2

Evaluation of the pfSeqGNM

Moreover, based on the work in Yang et al. (2009), we developed
the pfSeqGNM, where the original probability values, instead of
the binary values, are used as the inputs. The pfSeqGNM
method obtains ACC equals 0.493 based on the PDB951 dataset,
which improves by 0.04 over the classical SeqGNM. This con-
curs with Yang et al. (2009), where the structure-based param-
eter-free model, pfGNM, was shown to outperform the classical
structure-based GNM.

3.3.

Use of local predicted contacts improves prediction of
residue flexibility with pfSeqGNM

Inspired by Erman (2006) and Halle (2002), we investigate
whether the local predicted contacts, i.e.contacts in a sequence

Fig. 1. The ACCs between the native B

0

-factors and the B’-factors pre-

dicted with the classical SeqGNM on the PDB951 dataset. The ACC
values are calculated for varying probability cutoffs

499

Gaussian network model

at Uniwertytet Gdanski on May 28, 2014

http://bioinformatics.oxfordjournals.org/

Downloaded from

window, contribute to the flexibility expressed using B’-factors.
We developed linear regression model that takes the predicted
probability values of contacts, i.e. the diagonal elements in the
Kirchhoff matrix in the window as its input to compute the B’-
factor value of the central residue. Figure 2 shows the ACC
values that quantify the correlations between the outputs of the
linear regression model and the native B’-factor values for the
window sizes (shown on the x-axis) between 1 and 21 residues.
These results are based on 5-fold cross-validation (CV) (Zhang
et al.

, 2009) (Fig. 2A) and 10-fold cross-validation (Fig. 2B) on

the PDB951 dataset. The results for the 5-fold CV and 10-fold
CV are similar. For the 5-/10-fold CV, the ACC values improve
from 0.479/0.478, which corresponds to the window size of one
when the local neighborhood is not used, to 0.516/0.515 that
corresponds to the window size of seven. Use of larger window
sizes does not lead to further improvements. Consequently, the
window size of seven is selected. The corresponding linear regres-
sion model, which is trained on the entire PDB951 dataset, is as
follows:

^

B

0
i

¼

0:0579

pfSeq
i

3, i3

þ

0:0357

pfSeq
i

2, i2

þ

0:0512

pfSeq
i

1, i1

þ

0:2722

pfSeq
i

, i

þ

0:0722

pfSeq
iþ

1, iþ1

þ

0:0230

pfSeq
iþ

2, iþ2

þ

0:0569

pfSeq
iþ

3, iþ3

þ

0:0186

ð

10Þ

where

pfSeq
i

, i

is defined in Equation (7), and the window includes

three residues on both sides of the ith position. The regression
model has the largest coefficient for the central, ith residue,
which implies that, as expected, the contacts of this residue
have the strongest relation with its flexibility. The coefficients
for the neighboring residues are also positive, and they indicate
that the contacts of these residues have influence on the flexibility
of the ith residue.

We use this linear regression model to create a new Kirchhoff

matrix that is expressed in Equation (9), and the corresponding
GNM is referred to as the L-pfSeqGNM.

3.4

Comparative evaluation of the sequence- and struc-
ture-based prediction of residue flexibility

Table 1 shows the ACC values between the native B’-factors and
B’-factors predicted with two structure-based methods, the clas-
sical GNM and the pfGNM, and with two sequence-based meth-
ods, pfSeqGNM and L-pfSeqGNM. The predictions were

performed on the PDB951 and PDB748 datasets, and the cor-
responding ACC values are reported in the upper triangle and
the lower triangle in Table 1, respectively. The ACC value of
pfGNM is better than that of GNM for both datasets, which
agrees with Yang et al. (2009). Similarly, ACC of L-pfSeqGNM
is higher than that of pfSeqGNM, which confirms that the local
predicted contacts contribute to the prediction of residue flexi-
bility. The strong correlation of 0.94 between pfGNM and GNM
implies that these two structure-based methods generate similar
results. Analogous similarity is observed between L-pfSeqGNM
and pfSeqGNM, for which the predictions are correlated with
ACC at 0.93. This is a consequence of the fact that the former
approach extends the latter on by using a linear model.
Importantly, the difference in the predictive quality between
structure-based and sequence based methods is relatively small.
The ACC of L-pfSeqGNM (0.52 and 0.53 on the PDB951 and
PDB748 datasets, respectively) is close to that of GNM (0.56 and
0.58), on both datasets showing moderate correlations between
the predicted and native B’-factors.

Moreover,

the

structure-based

methods

(GNM

and

pfGNM) and the sequence-based methods (pfSeqGNM and
L-pfSeqGNM) have correlations at round 0.6, which suggests
that the sequence-based methods generate results that are rela-
tively similar to the structure-based methods. We plotted the
distributions of the correlation coefficient values of each se-
quence between the outputs of pfGNM and pfSeqGNM on
the PDB951 and PDB748 datasets; see Figure 3. We note that
the distributions for the PDB951 and PDB748 datasets are simi-
lar and that the majority of sequences have correlation coeffi-
cient values between 0.5 and 0.8, i.e. 83% of sequences in each of
the two datasets. Although the predictions generated by the
structure-based methods are better than those of the sequence-
based methods, the latter methods can be applied to a much
wider range of problems where the structural information is
unavailable.

3.5

Impact of the predictive quality of NNcon on the
prediction of residue flexibility with L-pfSeqGNM

The assessment of contact prediction uses two metrics, the ac-
curacy (Acc) and the coverage (Cov), which are widely used to

Table 1. The ACCs between the native B’-factors (NBF) and the B

0

-fac-

tors predicted by the structure-based GNM and pfGNM methods, and
by the sequence-based pfSeqGNM and L-pfSeqGNM methods

Method

NBF

GNM

pfGNM

pfSeqGNM

L-pfSeqGNM

NBF

1

0.557

0.593

0.493

0.517

GNM

0.584

1

0.940

0.592

0.589

pfGNM

0.621

0.941

1

0.635

0.627

pfSeqGNM

0.497

0.576

0.623

1

0.927

L-pfSeqGNM

0.526

0.587

0.625

0.927

1

Note

: The predictions were performed on the PDB951 and PDB748 datasets; the

corresponding ACC values are reported in the upper and the lower triangle, respect-
ively. The results in the last column, i.e. the ACCs between B

0

-factors predicted by

L-pfSeqGNM and other methods, are based on the 5-fold cross-validation on the
PDB951 dataset; the results using 10-fold CV are not shown, as they are virtually
identical.

Fig. 2. Strength of the relation between native B’-factors and the B’-fac-
tors predicted using the linear regression model computed from the local
predicted contacts, which is measured with the ACCs (y-axis). The ACC
values are calculated for varying window sizes (x-axis) based on 5-fold
cross-validation (panel A) and 10-fold cross-validation (panel B) on the
PDB951 dataset

500

H.Zhang and L.Kurgan

at Uniwertytet Gdanski on May 28, 2014

http://bioinformatics.oxfordjournals.org/

Downloaded from

evaluate the contact predictions in the CASP and the recent
studies (Di Lena et al., 2012; Eickholt and Cheng, 2012; Li
et al.

, 2011; Tegge et al., 2009). The accuracy is defined as the

number of correctly predicted residue–residue contacts divided
by the total number of top L/5 or L contact predictions, where L
is the length of the protein in residues. The coverage is the
number of correctly predicted residue–residue contacts divided
by the number of true contacts. The contact evaluation is com-
monly divided into three categories: short-range contacts for
which residue separation in sequence is 6 and 512, medium-
range contacts with separation 12 and 524 and long-range
contacts that are defined as having separation 24 residues.
Table 2 shows the predictive performance of the NNcon
method for short, medium and long-range contact prediction
on the PDB951 dataset. The accuracy (Acc) values for the dis-
tance cutoff of 8 A˚ are close to the results reported in recent
studies (Di Lena et al., 2012; Eickholt and Cheng, 2012; Li
et al.

, 2011; Tegge et al., 2009), but are markedly lower than

those of 12 A˚ case. For the distance cutoff of 12 A˚, especially
when considering top L predictions, NNcon yields accuracy of
0.750 and coverage of 0.467 for short-range contact, accuracy of
0.481 and coverage of 0.311 for medium-range contact. This
result supports our finding that the predicted contacts defined
at 12 A˚ result in better B-factor prediction than the cutoff of 8 A˚.

Similarly as in the recent works (Eickholt and Cheng, 2012;

Eickholt et al., 2011), we also calculated the number of contact
predictions that are close to a true contact. A predicted contact is
considered correct if a true residue–residue contact is within
residues for small values of . For example, for ¼ 1, a predicted
contact (i,j) is assumed correct if a true contact is at positions
(i,j), (i 1,j), (i,j 1) and (i 1, j 1). Table 2 lists the predictive
performance of NNcon on the PDB951 dataset for ¼ 1 and
¼

2. The results demonstrate that if an offset by one or two

residue is allowed ( ¼ 1 or 2), both the accuracy and the cover-
age are improved by a substantial margin. In the case of assessing
the top L contact predictions and when ¼ 2, the NNcon pre-
dictor yields relatively high accuracies of 0.991, 0.857 and 0.639
for the short-, medium- and long-range contacts, respectively.
We note that GNM and its variations use the local, in the se-
quence, residue–residue contacts. The fact that the contact pre-
dictions are rather accurate when allowing small offsets, which
are within the range of the residues used by these methods,

explains the relatively high correlations between the native
B-factors and the B-factors predicted by the sequence-based
L-pfSeqGNM, and between the outputs of structure-based
pfGNM and sequence-based pfSeqGNM. Similar observations
are true when evaluating the NNcon predictor on the PDB748
dataset; see Supplementary Table S1.

Figure 4 shows scatter plots of the average accuracy of the

NNcon predictor (i.e. the average over the three accuracy values
for the short, medium and long contacts for each chain) and the
ACC values between the native B’-factors and the B’-factors
predicted by L-pfSeqGNM on the PDB951 dataset. The figure
demonstrates lack of a strong linear relation between these two
metrics when considering evaluations for both the top L/5 pre-
dictions (Fig. 4A) and for the top L predictions (Fig. 4B). The
corresponding Pearson correlation coefficients between the aver-
age accuracies of NNcon and the ACC values of L-pfSeqGNM
for the top L/5 predictions and top L predictions are 0.15 and
0.19, respectively. Moreover, although the NNcon accuracies
have a wide range of values, from low at about 0.1 to high
values close to 0.9, the corresponding ACC values of
L-pfSeqGNM are always fairly high, i.e. significant majority of
the values are above 40.4. These observations demonstrate that
the proposed here sequence-based L-pfSeqGNM method does
not rely on the high quality of contact maps predicted by
NNcon. Our method can predict B-factors with good predictive
quality even when the predictions from NNcon have relatively
low accuracy; this could be explained by the results in Table 2
that suggest that correct contacts can be found with a small
offset in the sequence. A similar relation of the ACC values of

Table 2. The predictive performance of NNcon for short, medium and
long-range contact predictions on the PDB951 dataset with the distance
cutoffs of 8 A˚ and 12 A˚, respectively

Evaluation criteria

Contact
range

8 A˚

12 A˚

Acc

Cov

Acc

Cov

Top L/5

Short

0.408

0.253

0.892

0.111

Medium

0.321

0.153

0.642

0.084

Long

0.199

0.029

0.463

0.017

Top L/5, ¼ 1

Short

0.776

0.511

0.980

0.124

Medium

0.560

0.304

0.864

0.116

Long

0.362

0.054

0.650

0.024

Top L/5, ¼ 2

Short

0.923

0.606

0.999

0.127

Medium

0.715

0.371

0.922

0.126

Long

0.447

0.068

0.712

0.027

Top L

Short

0.203

0.620

0.750

0.467

Medium

0.170

0.398

0.481

0.311

Long

0.119

0.088

0.352

0.062

Top L, ¼ 1

Short

0.581

0.998

0.949

0.603

Medium

0.407

0.883

0.765

0.507

Long

0.260

0.196

0.558

0.099

Top L, ¼ 2

Short

0.826

1.000

0.991

0.631

Medium

0.555

0.973

0.857

0.570

Long

0.351

0.265

0.639

0.114

Note

: Value of determines an offset by positions in the sequence that is allowed

to consider a given prediction correct.

Fig. 3. The distributions of CC values between the outputs of pfGNM
and pfSeqGNM for individual sequences on the PDB951 and PDB748
datasets. The frequencies/fractions of sequences are shown using CC
values binned using 0.1 wide intervals

501

Gaussian network model

at Uniwertytet Gdanski on May 28, 2014

http://bioinformatics.oxfordjournals.org/

Downloaded from

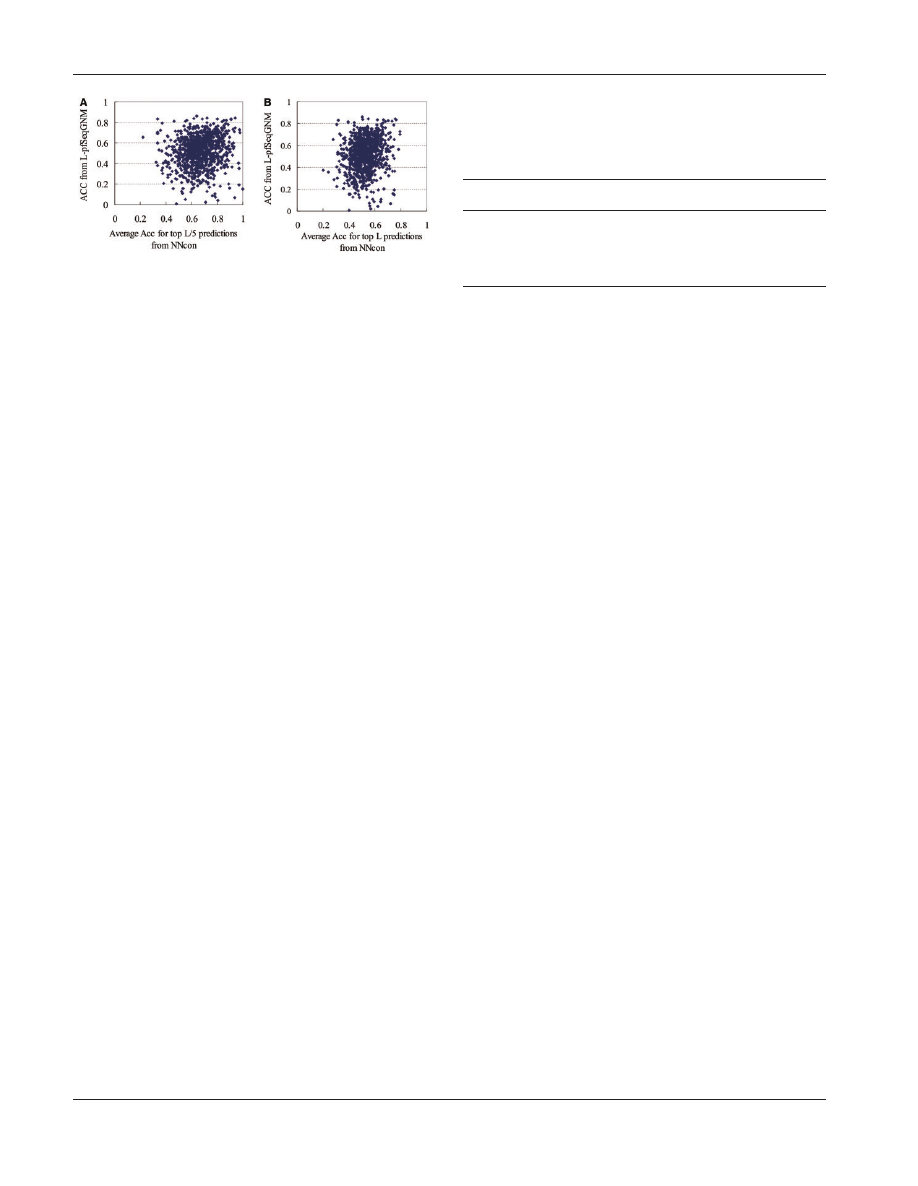
L-pfSeqGNM with the average Acc values of NNcon is true on
the PDB748 dataset, see Supplementary Figure S1.

3.6

Sequence-based determination of collective residue
motions

One of the key advantages of the SeqGNM is its ability to gen-
erate the cross-correlations of residue fluctuations and to de-
scribe the correlated motions of residues in a given protein,
particularly when the structure of this protein is unknown. The
cross-correlations express the strength of the collective motions
for a given pair of residues. They are useful in understanding
long-range propagation of motion and large domain movements,
which are relevant to protein function. Their applications have
been recently widely explored (Bahar et al., 1999; Doruker et al.,
2006; Jiang et al., 2011; Marcos et al., 2011). The cross-
correlation between any two residues is computed from the
Kirchhoff matrix. We compute the ACCs of the cross-
correlations of residue fluctuations for all pairs of methods
among the considered four GNMs on the PDB951 and
PDB748 datasets; see Table 3. The ACC values are 40.7 for
both datasets, which indicates that the cross-correlation matrices
generated by the four methods are similar. At the same time, the
SeqGNMs, i.e.pfSeqGNM and L-pfSeqGNM, can be used to
explore the collective motions for proteins with unknown struc-
tures, which allows for a wider range of applications and targets.

3.7

Case studies

We demonstrate and compare predictions of the considered se-
quence- and structure-based GNMs for three proteins: bovine

-lactoglobulin (lg, PDBid: 1B8E, chain A) (Oliveira et al.,

2001), histamine-binding protein from female brown ear
Rhipicephalus appendiculatus

tick (Ra-HBP, PDBid: 1QFT,

chain A) (Paesen et al., 1999) and the quorum-sensing protein
TraM (PDBid: 1UPG, chain A) (Vannini et al., 2004). lg is a
prominent member of the lipocalin family, a large group of pro-
teins involved in the transport of small hydrophobic molecules,
and has been widely used for protein-folding dynamics and ag-
gregation modeling (Arnaudov and de Vries, 2006; Bello et al.,
2011, 2012; Krebs et al., 2009) due to its abundant availability in
bovine milk. Ra-HBP binds histamine with high affinity and
specificity, and the histamine binding proteins are currently

investigated as potential therapeutic agents for the treatment of
various diseases (Mans, 2005). TraM protein inhibits the activity
of its associated LuxR-type transcription factor TraR in several
different microbial taxa, and is often required to maintain the
quorum-sensing mechanism in the inactive state (Chen et al.,
2006, 2007). Ra-HBP shares the same family (i.e. retinol binding
protein-like) in the Structural Classification of Proteins (SCOP)
database (Murzin et al., 1995) and has low-sequence identity
[525%, measured with BLASTCLUST (Altschul et al., 1997)]
with the lg protein. Moreover, lg and Ra-HBP have similar
B’-factor profiles, whereas the B’-factor profile of the third pro-
tein Tram is different from these two proteins, where lg and the
Ra-BHP have several flexible segments and TraM is mostly rigid.

Figure 5 compares the native B’-factor (normalized native

B-factor) profiles and the B’-factors predicted with GNM,
pfGNM, pfSeqGNM and L-pfSeqGNM. For lg, the correl-
ation coefficient values between the native B’-factors and the
B’-factors predicted with GNM, pfGNM, pfSeqGNM and
L-pfSeqGNM are 0.624, 0.648, 0.610 and 0.611, respectively.
The coefficients are 0.861, 0.858, 0.558 and 0.658, respectively,
for the Ra-BHP. These two results taken together suggest that
the proposed SeqGNMs can produce different and high-quality
B’-factor profiles for proteins in the same family but with differ-
ent sequences. Similarly high values of coefficients that equal
0.651, 0.654, 0.788 and 0.769, respectively, were obtained for
the TraM protein. These case studies demonstrate that all four
B’-factor prediction models correctly identified the flexible re-
gions (regions with the high-positive B’-factor values) and the
rigid regions (with low-negative B’-factor values) along the
three sequences.

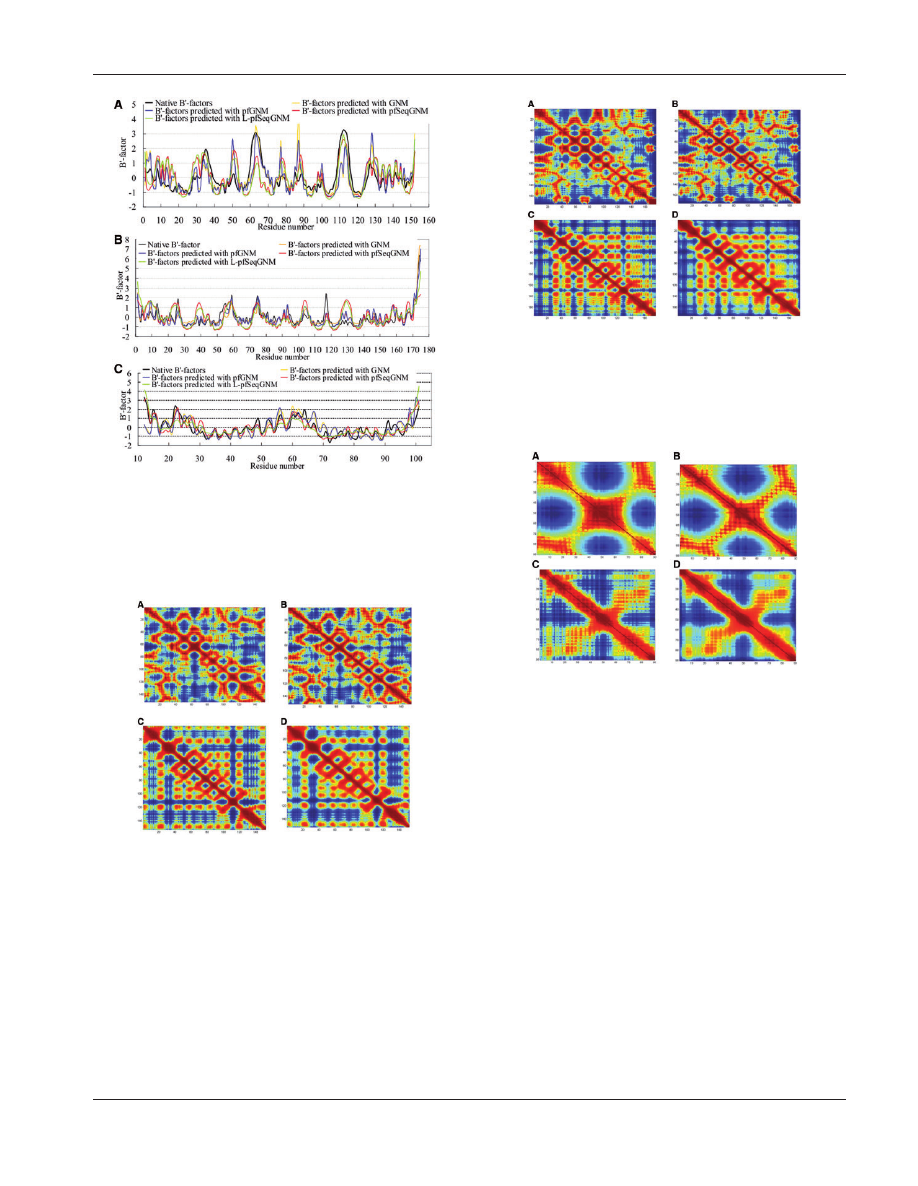
Figures 6, 7 and 8 show correlation maps of residue fluctu-

ations that are computed with the GNM (panel A), pfGNM
(panel B), pfSeqGNM (panel C) and L-pfSeqGNM (panel D)
methods for the three proteins. The colors range between red
(which denoted strong positive correlations) and blue (strong
negative correlations). Currently, there are no experimentally
derived correlation maps, except for the diagonal terms that cor-
respond to the B-factors, which could be used as a reference.
However, the similarity between the four maps (for each of the
three proteins) indicates that the SeqGNMs provide a viable al-
ternative to the maps generated from the structure.

Table 3. The ACCs between the cross-correlations of residue fluctuations
generated by the four considered GNMs on the PDB951 and PDB748
datasets; the corresponding ACC values are reported in the upper triangle
and the lower triangle, respectively

Method

GNM

pfGNM

pfSeqGNM

L-pfseqGNM

GNM

1

0.810

0.717

0.716

pfGNM

0.813

1

0.955

0.960

pfSeqGNM

0.715

0.954

1

0.993

L-pfSeqGNM

0.716

0.960

0.993

1

Note

: The results in the last column, i.e. the ACCs between the cross-correlations of

residue fluctuations generated by L-pfSeqGNM and other methods are based on the
5-fold cross-validation; the results based on the 10-fold CV are not shown, as they
are virtually identical

Fig. 4. The scatter plots of the average ACC values (x-axis) from NNcon
and ACC values (y-axis) from L-pfSeqGNM with the contact cutoff of
12 A˚ for top L/5 contact predictions (panel A) and top L predictions
(panel

B).

Each

point

corresponds

to

one

protein

from

the

PDB951dataset

502

H.Zhang and L.Kurgan

at Uniwertytet Gdanski on May 28, 2014

http://bioinformatics.oxfordjournals.org/

Downloaded from

Although these three case studies should not be taken as typ-

ical, they demonstrate (in agreement with our benchmarking re-
sults) that SeqGNMs could be applied to provide useful
prediction of the B’-factors and correlation maps, and that
these predictions have comparable quality with the predictions
obtained from the structure-based GNMs.

4

DISCUSSION

The B-factors reflect the residue fluctuations and static, dynamic
and lattice disorders. However, they depend on the experimental
resolution, crystal contacts and refinement procedures, which is
why the B-factor profiles of homologous protein are shown to be
correlated with each other with the ACC of 0.80 (Yuan et al.,
2005). This constitutes an approximate upper limit for the pre-
diction of the B-factor values, which applies to the considered
GNM-based models. Yang et al. (2009) have recently proposed a
new distance-dependent (parameter-free) GNM in which residue
pairs are weighted by the inverse square of their distances. This
pfGNM method had been shown to outperform the classical
distance cutoff-based GNM in prediction the B-factors. Here,
the

proposed

SeqGNM

methods,

pfSeqGNM

and

L-pfSeqGNM, predict the B-factors with comparably (to the
structure-based method) high correlations equal 0.49 and 0.52
on the PDB951 dataset, and 0.50 and 0.53 on the PDB748

Fig. 5. The native B’-factors and the B’-factors predicted with the GNM,
pfGNM, pfSeqGNM and L-pfSeqGNM methods for (A) -lactoglobulin
(PDBid: 1B8E, chain A), (B) the histamine-binding protein Ra-HBP
(PDBid: 1QFT, chain A) and (C) the quorum-sensing protein TraM
(PDBid: 1UPG, chain A)

Fig. 6. The maps of the cross-correlations of residue fluctuations for the

-lactoglobulin protein (PDBid: 1B8E, chain A) computed with (A)

GNM, (B) pfGNM, (C) pfSeqGNM and (D) L-pfSeqGNM methods.
The colors range between red (strong positive correlations) and blue
(strong negative correlations)

Fig. 7. The maps of the cross-correlations of residue fluctuations for the
histamine-binding protein Ra-HBP (PDBid: 1QFT, chain A) computed
with (A) GNM, (B) pfGNM, (C) pfSeqGNM and (D) L-pfSeqGNM
methods. The colors range between red (strong positive correlations)
and blue (strong negative correlations)

Fig. 8. The maps of the cross-correlations of residue fluctuations for the
quorum-sensing protein TraM (PDBid: 1UPG, chain A) computed with
(A) GNM, (B) pfGNM, (C) pfSeqGNM and (D) L-pfSeqGNM methods.
The colors range between red (strong positive correlations) and blue
(strong negative correlations)

503

Gaussian network model

at Uniwertytet Gdanski on May 28, 2014

http://bioinformatics.oxfordjournals.org/

Downloaded from

dataset, respectively. We demonstrate that the pfGNM is also
advantageous for our sequence-based approach, i.e. we show
that the pfSeqGNM outperforms the classical SeqGNMs.
Furthermore, motivated by the findings concerning the impact
of local contact density and local solvent accessibility on the
residue flexibility expressed with the B-factors (Halle, 2002;
Zhang et al., 2009), we use linear regression to model the rela-
tion between the local predicted contacts and the residue
flexibility. This led to the development of an improved
pfSeqGNM that uses the local contacts, which is called
L-pfSeqGNM. Our empirical results suggest that this model pro-
vides useful predictions of the residue flexibility and the collective
residue motions.

The key advantage of the SeqGNM is that it can be applied to

proteins with unknown structures and known sequences, which
number in millions. In contrast, the existing and widely adopted
structure-based GNMs are limited to a much smaller subpopula-
tion of proteins with known structure. Our model finds numer-
ous applications in modeling of protein motion, conformational
changes, protein–protein interactions and protein functions, to
name just a few.

ACKNOWLEDGEMENT

The authors would like to thank Dr Cheng for providing the
training dataset used in NNcon program.

Funding

: National Natural Science Foundation of China (grant

no. 61170099 and 610033074 to H.Z.), the Zhejiang Provincial
Natural Science Foundation of China (grant no. Y1110840,
Y1090165, Y1110644 and Y1110969 to H.Z.) and NSERC
Discovery grant (to L.K.).

Conflict of Interest

: none declared.

REFERENCES

Altschul,S.F. et al. (1997) Gapped BLAST and PSI-BLAST: a new generation of

protein database search programs. Nucleic Acids Res., 25, 3389–3402.

Arnaudov,L.N. and de Vries,R. (2006) Strong impact of ionic strength on the kin-

etics of fibrilar aggregation of bovine -lactoglobulin. Biomacromolecules, 7,
3490–3498.

Atilgan,A.R. et al. (2001) Anisotropy of fluctuation dynamics of proteins with an

elastic network model. Biophys. J., 80, 505–515.

Bahar,I. and Rader,A.J. (2005) Coarse-grained normal mode analysis in structural

biology. Curr. Opin. Struct. Biol., 15, 586–592.

Bahar,I. et al. (1997) Direct evaluation of thermal fluctuations in proteins using a

single-parameter harmonic potential. Fold. Des., 2, 173–181.

Bahar,I. et al. (1999) Collective motions in HIV-1 reverse transcriptase: examination

of flexibility and enzyme function. J. Mol. Biol., 285, 1023–1037.

Bakan,A. and Bahar,I. (2009) The intrinsic dynamics of enzymes plays a dominant

role in determining the structural changes induced upon inhibitor binding. Proc.
Natl Acad. Sci. USA

, 106, 14349–14354.

Bello,M. et al. (2011) Energetics of ligand recognition and self-association of bovine

-lactoglobulin: differences between variants A and B. Biochemistry, 50,

151–161.

Bello,M. et al. (2012) Structure and dynamics of -lactoglobulin in complex with

dodecyl sulfate and laurate: a molecular dynamics study. Biophys. Chem., 165–
166, 79–86.

Berman,H.M. et al. (2000) The protein data bank. Nucleic Acids Res., 28, 235–242.
Bhalla,J. et al. (2006) Local flexibility in molecular function paradigm. Mol. Cell.

Proteomics

, 5, 1212–1223.

Bornot,A. et al. (2011) Predicting protein flexibility through the prediction of local

structures. Proteins, 79, 839–852.

Chen,G. et al. (2006) Crystal structure and mechanism of TraM2, a second quorum-

sensing antiactivator of Agrobacterium tumefaciens strain A6. J. Bacteriol., 188,
8244–8251.

Chen,G. et al. (2007) Structural basis for antiactivation in bacterial quorum sensing.

Proc. Natl Acad. Sci. USA

, 104, 16474–16479.

Cheng,J. and Baldi,P. (2007) Improved residue contact prediction using support

vector machines and a large feature set. BMC Bioinformatics, 8, 113.

Ding,W. et al. (2013) CNNcon: improved protein contact maps prediction using

cascaded neural networks. PLoS One, 8, e61533.

Dobbins,S.E. et al. (2008) Insights into protein flexibility: the relationship between

normal modes and conformational change upon protein-protein docking. Proc.
Natl Acad. Sci. USA

, 105, 10390–10395.

Doruker,P. et al. (2006) Collective dynamics of EcoRI-DNA complex by elastic

network model and molecular dynamics simulations. J. Biomol. Struct. Dyn., 24,
1–16.

Eickholt,J. and Cheng,J. (2012) Predicting protein residue-residue contacts using

deep networks and boosting. Bioinformatics, 28, 3066–3072.

Eickholt,J. et al. (2011) A conformation ensemble approach to protein residue-resi-

due contact. BMC Struct. Biol., 11, 38.

Eisenmesser,E.Z. et al. (2005) Intrinsic dynamics of an enzyme underlies catalysis.

Nature

, 438, 117–121.

Erman,B. (2006) The gaussian network model: precise prediction of residue fluctu-

ations and application to binding problems. Biophys. J., 91, 3589–3599.

Haliloglu,T. et al. (2008) Prediction of binding sites in receptor-ligand complexes

with the Gaussian network model. Phys. Rev. Lett., 100, 228102.

Haliloglu,T. and Erman,B. (2009) Analysis of correlations between energy and resi-

due fluctuations in native proteins and determination of specific sites for bind-
ing. Phys. Rev. Lett., 102, 088103.

Halle,B. (2002) Flexibility and packing in proteins. Proc. Natl Acad. Sci. USA, 99,

1274–1279.

Hirose,S. et al. (2010) Prediction of protein motions from amino acid sequence and

its application to protein-protein interaction. BMC Struct. Biol., 10, 20.

Jiang,J.

et

al

.

(2011)

Large

collective

motions

regulate

the

functional

properties of glutamate transporter trimers. Proc. Natl Acad. Sci. USA, 108,
15141–15146.

Keskin,O. et al. (2002) Molecular mechanisms of chaperonin GroEL-GroES func-

tion. Biochemistry, 41, 491–501.

Kim,J.I. et al. (2011) Domain decomposition-based structural condensation of large

protein structures for understanding their conformational dynamics. J. Comput.
Chem.

, 32, 161–169.

Krebs,M.R. et al. (2009) Amyloid fibril-like structure underlies the aggregate struc-

ture across the pH range for -lactoglobulin. Biophys. J., 96, 5013–5019.

Kundu,S. et al. (2002) Dynamics of proteins in crystals: comparison of experiment

with simple models. Biophys. J., 83, 723–732.

Kurkcuoglu,O. and Bates,P.A. (2010) Mechanism of cohesin loading onto chromo-

somes: a conformational dynamics study. Biophys. J., 99, 1212–1220.

Di Lena,P. et al. (2012) Deep architectures for protein contact map prediction.

Bioinformatics

, 28, 2449–2457.

Li,Y. et al. (2011) Predicting residue-residue contacts using random forest models.

Bioinformatics.

, 27, 3379–3384.

Lin,C.P. et al. (2008) Deriving protein dynamical properties from weighted protein

contact number. Proteins, 72, 929–935.

Mans,B.J. (2005) Tick histamine-binding proteins and related lipocalins: potential

as therapeutic agents. Curr. Opin. Investig. Drugs, 6, 1131–1135.

Marcos,E. et al. (2011) Changes in dynamics upon oligomerization regulate sub-

strate binding and allostery in amino acid kinase family members. PLoS
Comput. Biol.

, 7, e1002201.

Mendez,R. and Bastolla,U. (2010) Torsional network model: normal modes in tor-

sion angle space better correlate with conformation changes in proteins. Phys.
Rev. Lett.

, 104, 228103.

Ming,D. et al. (2002) How to describe protein motion without amino acid sequence

and atomic coordinates. Proc. Natl Acad. Sci. USA, 99, 8620–8625.

Monastyrskyy,B. et al. (2011) Evaluation of residue-residue contact predictions in

CASP9. Proteins, 79 (Suppl. 10), 119–125.

Murzin,A.G. et al. (1995) SCOP: a structural classification of proteins database for

the investigation of sequences and structures. J. Mol. Biol., 247, 536–540.

Noguchi,T. and Akiyama,Y. (2003) PDB-REPRDB: a database of representative

protein chains from the Protein Data Bank (PDB) in 2003. Nucleic Acids Res.,
31, 492–493.

Oliveira,K.M. et al. (2001) Crystal structures of bovine beta-lactoglobulin in the

orthorhombic space group C222(1). Structural differences between genetic

504

H.Zhang and L.Kurgan

at Uniwertytet Gdanski on May 28, 2014

http://bioinformatics.oxfordjournals.org/

Downloaded from

variants A and B and features of the Tanford transition. Eur. J. Biochem., 268,
477–483.

Paesen,G.C. et al. (1999) Tick histamine-binding proteins: isolation, cloning, and

three-dimensional structure. Mol. Cell, 3, 661–671.

Rueda,M. et al. (2007) A consensus view of protein dynamics. Proc. Natl Acad. Sci.

USA

, 104, 796–801.

Schlessinger,A. and Rost,B. (2005) Protein flexibility and rigidity predicted from

sequence. Proteins, 61, 115–126.

Song,G. and Jernigan,R.L. (2007) vGNM: a better model for understanding the

dynamics of proteins in crystals. J. Mol. Biol., 369, 880–893.

Srivastava,A. and Granek,R. (2013) Cooperativity in thermal and force-induced

protein unfolding: integration of crack propagation and network elasticity
models. Phys. Rev. Lett., 110, 138101.

Szarecka,A. et al. (2007) Dynamics of firefly luciferase inhibition by general anes-

thetics: Gaussian and anisotropic network analyses. Biophys. J., 93, 1895–1905.

Tegge,A.N. et al. (2009) NNcon: improved protein contact map prediction using

2D-recursive neural networks. Nucleic Acids Res., 37, W515–W518.

Tuzmen,C. and Erman,B. (2011) Identification of ligand binding sites of proteins

using the Gaussian network model. PLoS One, 6, e16474.

Vannini,A. et al. (2004) Crystal structure of the quorum-sensing protein TraM and

its interaction with the transcriptional regulator TraR. J. Biol. Chem., 279,
24291–24296.

Wang,Z. and Xu,J. (2013) Predicting protein contact map using evolutionary and

physical constraints by integer programming. Bioinformatics, 29, i266–i273.

Wieninger,S.A. et al. (2011) ATP binding enables broad antibiotic selectivity

of aminoglycoside phosphotransferase(3

0

)-IIIa: an elastic network analysis.

J. Mol. Biol.

, 409, 450–465.

Yang,L. et al. (2007a) How well can we understand large-scale protein motions

using normal modes of elastic network models? Biophys. J., 93, 920–929.

Yang,L. et al. (2008) Close correspondence between the motions from principal

component analysis of multiple HIV-1 protease structures and elastic network
modes. Structure, 16, 321–330.

Yang,L. et al. (2009) Protein elastic network models and the ranges of cooperativity.

Proc. Natl Acad. Sci. USA

, 106, 12347–12352.

Yang,L.W. and Bahar,I. (2005) Coupling between catalytic site and collective dy-

namics: a requirement for mechanochemical activity of enzymes. Structure, 13,
893–904.

Yang,L.W. et al. (2007b) Insights into equilibrium dynamics of proteins from com-

parison of NMR and X-ray data with computational predictions. Structure, 15,
741–749.

Yuan,Z. et al. (2005) Prediction of protein B-factor profiles. Proteins, 58, 905–912.
Zhang,H. et al. (2009) On the relation between residue flexibility and local solvent

accessibility in proteins. Proteins, 76, 617–636.

Zheng,W. (2008) A unification of the elastic network model and the Gaussian net-

work model for optimal description of protein conformational motions and
fluctuations. Biophys. J., 94, 3853–3857.

Zheng,W. (2010) Anharmonic normal mode analysis of elastic network model im-

proves the modeling of atomic fluctuations in protein crystal structures. Biophys.
J.

, 98, 3025–3034.

Zheng,W. and Brooks,B.R. (2005) Normal-modes-based prediction of protein con-

formational changes guided by distance constraints. Biophys. J., 88, 3109–3117.

Zheng,W. and Doniach,S. (2003) A comparative study of motor-protein motions by

using a simple elastic-network model. Proc. Natl Acad. Sci. USA, 100,
13253–13258.

Zhu,F. and Hummer,G. (2010) Pore opening and closing of a pentameric ligand-

gated ion channel. Proc. Natl Acad. Sci. USA, 107, 19814–19819.

Zhuravleva,A. et al. (2007) Propagation of dynamic changes in barnase upon bind-

ing of barstar: an NMR and computational study. J. Mol. Biol., 367, 1079–1092.

505

Gaussian network model

at Uniwertytet Gdanski on May 28, 2014

http://bioinformatics.oxfordjournals.org/

Downloaded from