1

Problematyka wykładu

•Zjawisko hazardu

•Układy arytmetyczne

•Układy konwersji kodów

•Multipleksery i demultipleksery

•Wprowadzenie

2

Wprowadzenie

• określenie funkcji logicznej odpowiednio do postawionych

wymagań np. za pomocą tablicy stanów (tablicy prawdy);

• przeprowadzenie procesu minimalizacji funkcji logicznej np.

przy użyciu tablic Karnaugha lub metodą algebraiczną;

• sporządzenie schematu układu, odpowiadającego

zminimalizowanej formie boolowskiej;

• optymalizacja konfiguracji schematowej.

Kolejność postępowania przy syntezie kombinacyjnego układu
logicznego:

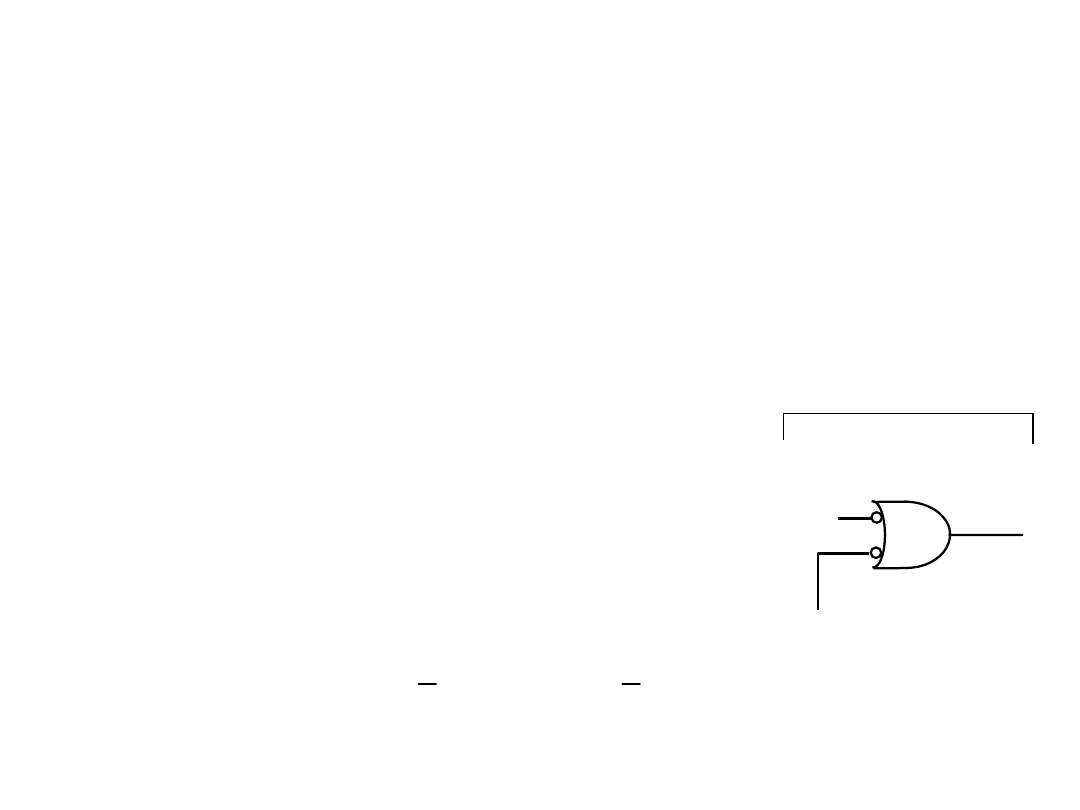
3

Wprowadzenie

Synteza układu opisanego formą sumacyjną, reguły stosowania
symboli funktorów równoważnych dla NAND:

1. bramkę wejściową, na której wyjściu otrzymuje się stany lub

poziomy logiczne realizujące pożądaną funkcję, określa się
jako reprezentującą pierwszy (nieparzysty) poziom układu.
Graficznym symbolem tej bramki jest symbol DOR;

POZIOMY UKŁADU

1

F

1

x

= +

+

1

2

3

4

5

*(

* )

F

x

x

x

x

x

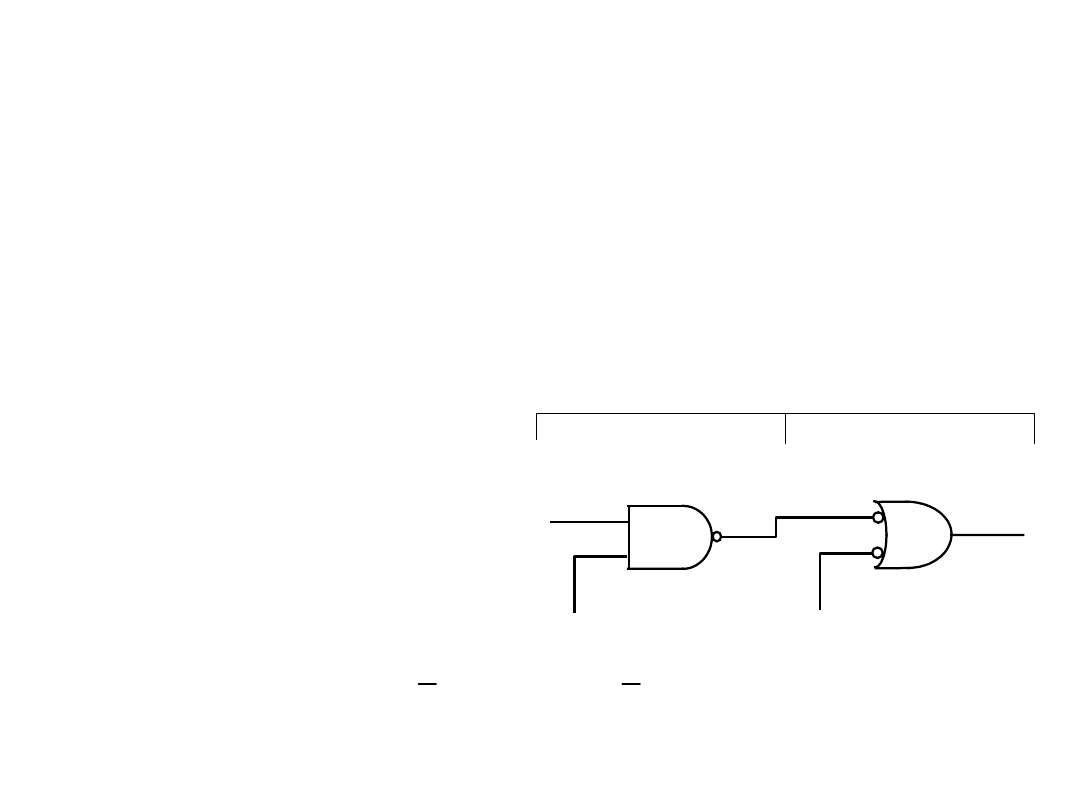
4

Wprowadzenie

2. bramki których wyjścia są przyłączone do wejść bramki

wyjściowej, określa się jako reprezentujące drugi (parzysty)
poziom układu. Graficznymi symbolami tych bramek są
symbole NAND;

Synteza układu opisanego formą sumacyjną, reguły stosowania
symboli funktorów równoważnych dla NAND:

POZIOMY UKŁADU

2

2

x

1

F

1

x

= +

+

1

2

3

4

5

*(

* )

F

x

x

x

x

x

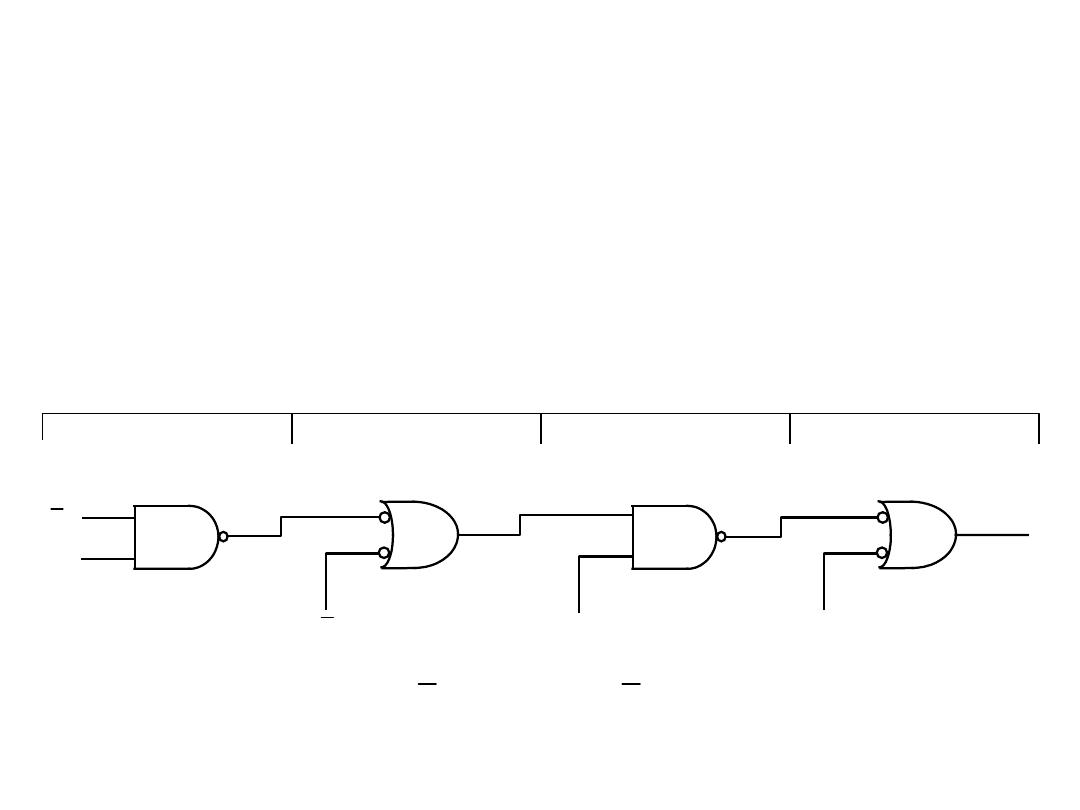
5

Wprowadzenie

3. dalsze poprzedzające bramki reprezentują odpowiednio dalsze

nieparzyste i parzyste poziomy, przy czym na poziomach
nieparzystych stosuje się symbole DOR, a na poziomach
parzystych symbole NAND;

Synteza układu opisanego formą sumacyjną, reguły stosowania
symboli funktorów równoważnych dla NAND:

POZIOMY UKŁADU

F

1

1

x

2

2

x

4

5

x

4

x

3

3

x

= +

+

1

2

3

4

5

*(

* )

F

x

x

x

x

x

6

Wprowadzenie

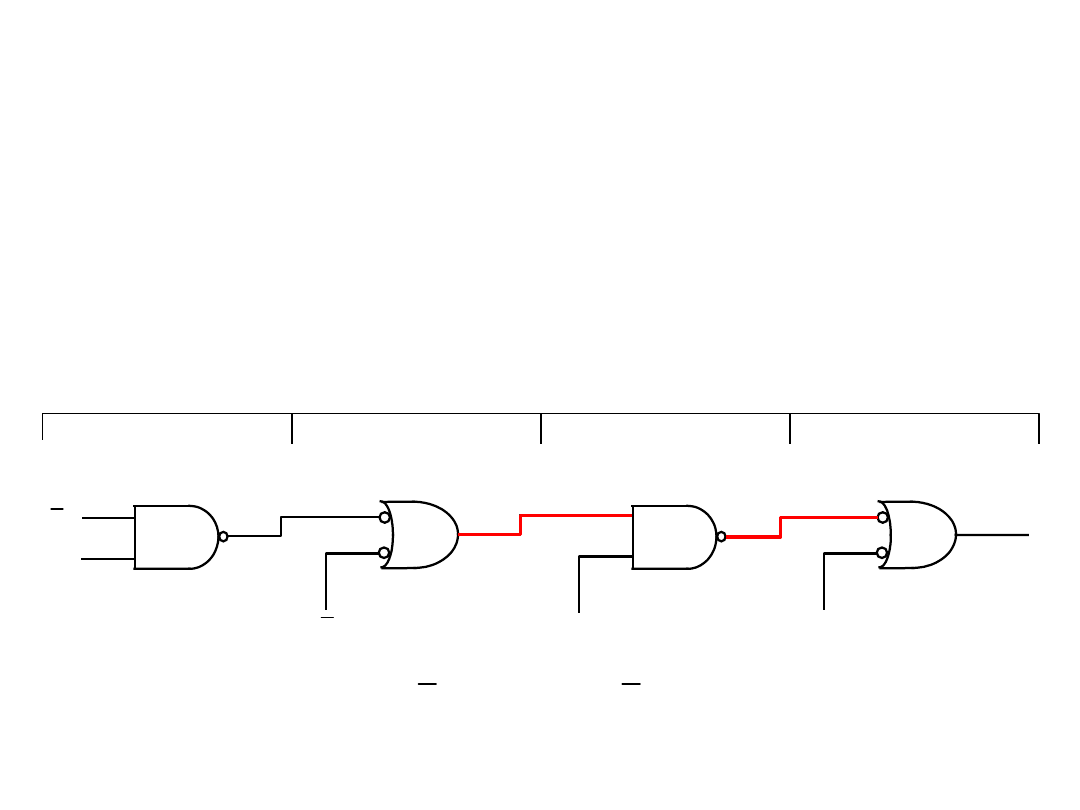
4. w zasadzie każda linia połączeniowa między wyjściem jednej

bramki a wejściem drugiej powinna mieć na obydwu
końcach symbole wskaźnika negacji lub nie powinna ich mieć
w ogóle;

Synteza układu opisanego formą sumacyjną, reguły stosowania
symboli funktorów równoważnych dla NAND:

POZIOMY UKŁADU

F

1

1

x

2

2

x

3

3

x

4

5

x

4

x

= +

+

1

2

3

4

5

*(

* )

F

x

x

x

x

x

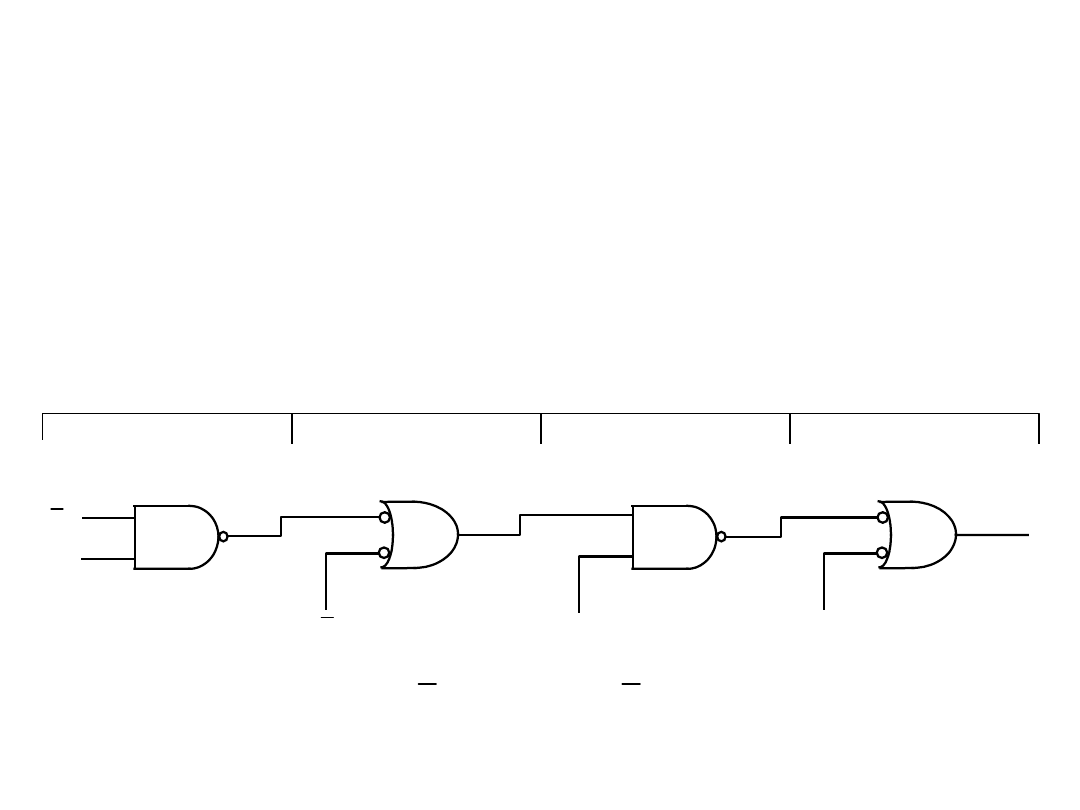
7

Wprowadzenie

5. zmienne wprowadzane na wejścia ze wskaźnikami negacji są

reprezentowane w formie boolowskiej przez swe dopełnienia;

Synteza układu opisanego formą sumacyjną, reguły stosowania
symboli funktorów równoważnych dla NAND:

POZIOMY UKŁADU

F

1

1

x

2

2

x

3

3

x

4

5

x

4

x

= +

+

1

2

3

4

5

*(

* )

F

x

x

x

x

x

6. zmienne wprowadzane na wejścia bez wskaźników negacji są

reprezentowane w formie boolowskiej bez dopełnienia.

1

x

1

x

2

x

2

x

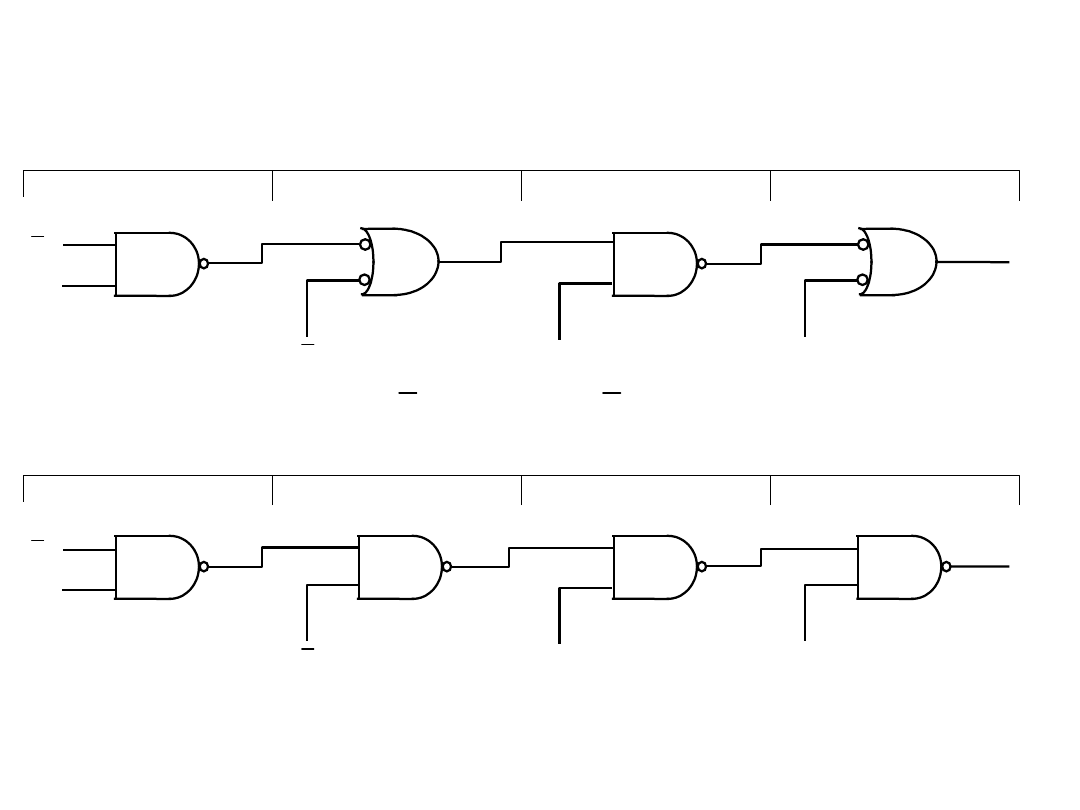
8

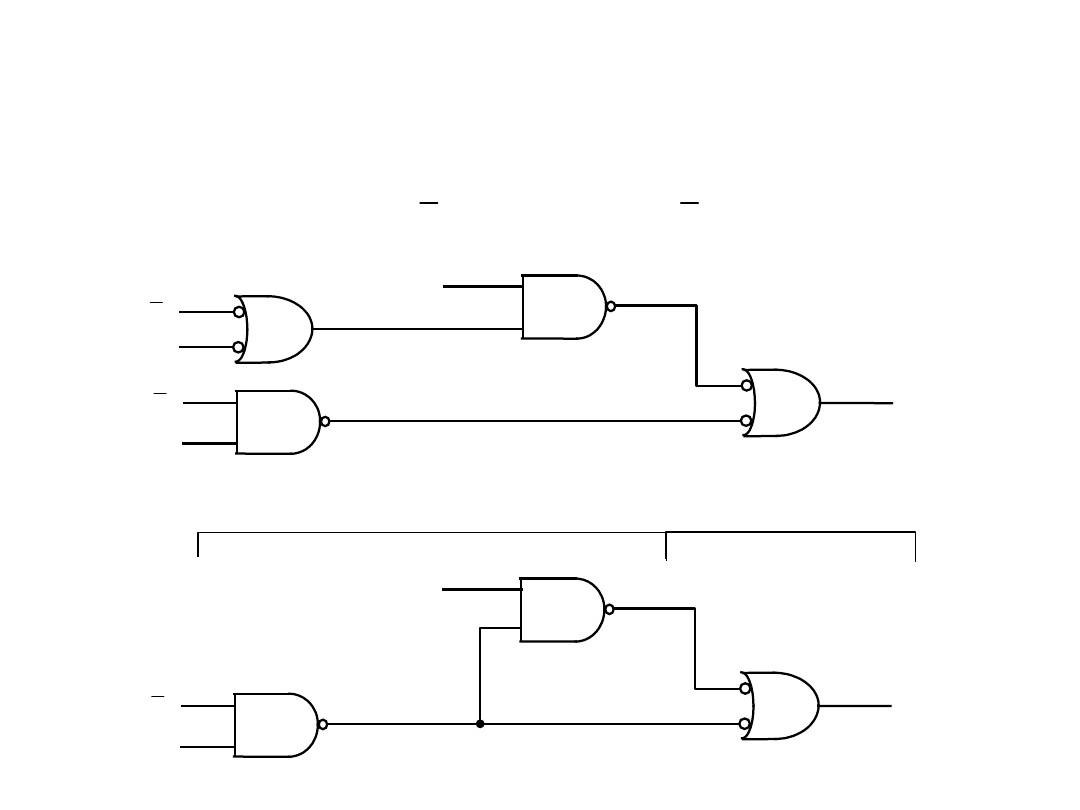
Wprowadzenie

POZIOMY UKŁADU

F

1

1

x

2

2

x

3

3

x

4

5

x

4

x

= +

+

1

2

3

4

5

*(

* )

F

x

x

x

x

x

F

1

1

x

2

2

x

3

3

x

4

5

x

4

x

9

Wprowadzenie

=

+

+

1

2

3

1

2

*

*(

)

F

x x

x

x

x

F

3

x

2

x

1

x

2

x

1

x

1

2

POZIOMY UKŁADU

F

3

x

2

x

1

x

Przykład odstępstwa od reguły

4-tej

10

Wprowadzenie

Do optymalizacji układów kombinacyjnych (reguła 4-ta)

najczęściej są stosowane następujące kryteria:

1.minimalna

złożoność

układowa;

4. maksymalna niezawodność.

3. minimalny koszt;

2. minimalne opóźnienie propagacji;

11

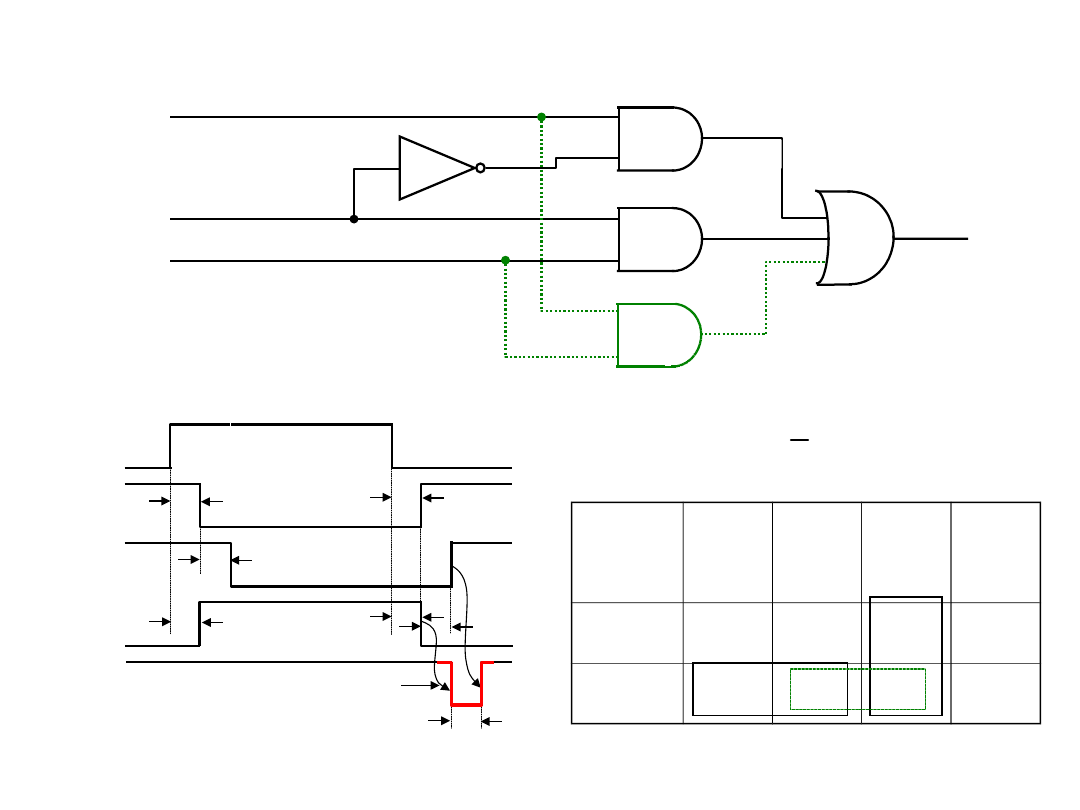
Hazard

Przyczyny powstania zjawiska hazardu:

1. gdy przynajmniej jeden sygnał wejściowy dochodzi do wyjścia

drogami
o różnych opóźnieniach;

3. gdy układ zapewnia dla wszystkich sygnałów wejściowych drogi

o jednakowych opóźnieniach, lecz sygnały te zmieniają swe stany
logiczne niejednocześnie.

2. gdy jednocześnie ulegają zmianie dwa lub więcej sygnałów

wejściowych
i przechodzą one do wyjścia drogami o różnych opóźnieniach;

12

1

0

1

1

1

0

1



0



1

 1

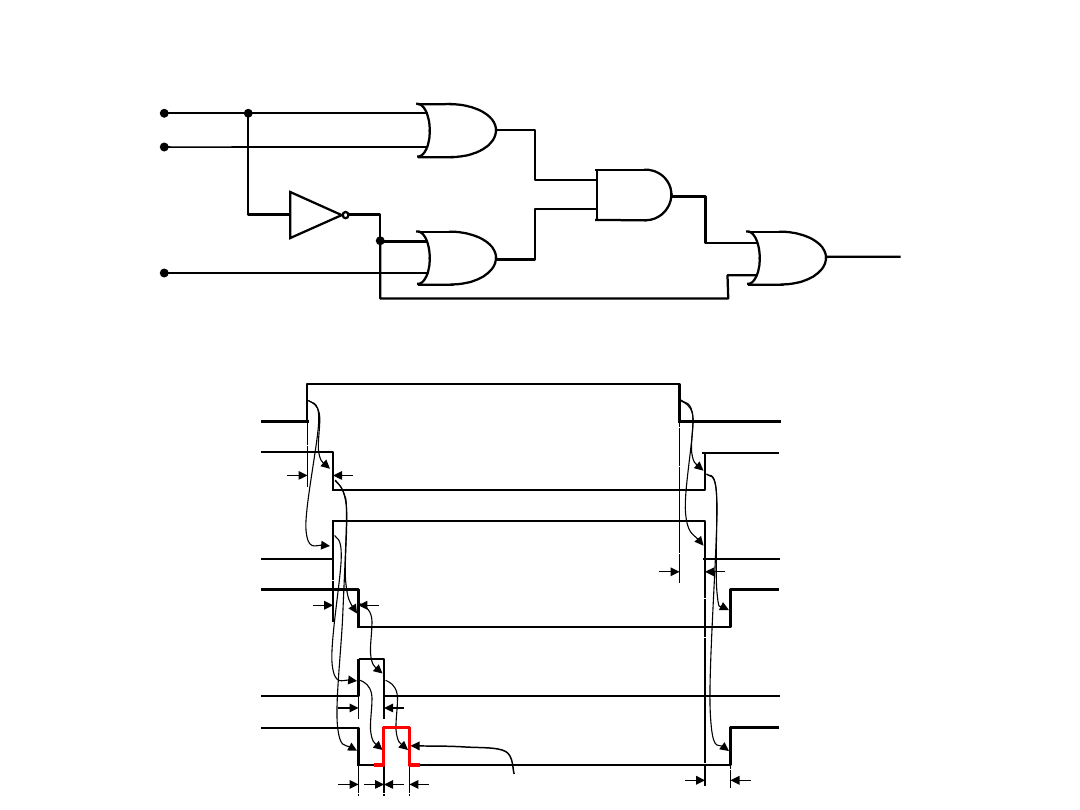
Zjawisko hazardu statycznego

F

3

x

2

x

1

x

F

1

F

2

F

3

=

=

1

3

1

x

x

2

x

F

1

F

2

F

3

F

t

t

Hazard statyczny

w 1

t

t

t

t

t

x

1

x

0

x

2

00

01

11

10

0

1

1

1

1

1

=

+

1

2

2

3

*

*

F

x x

x x

 0

1 0

0

 1

1

 0

1

 0

0

1

0

0

 1

0

 1

13

F

3

x

2

x

1

x

F

1

F

2

F

4

F

3

0

0

0

1

1

0

0

1

1

0

0

1

1

0

1

0

1

0

0

1

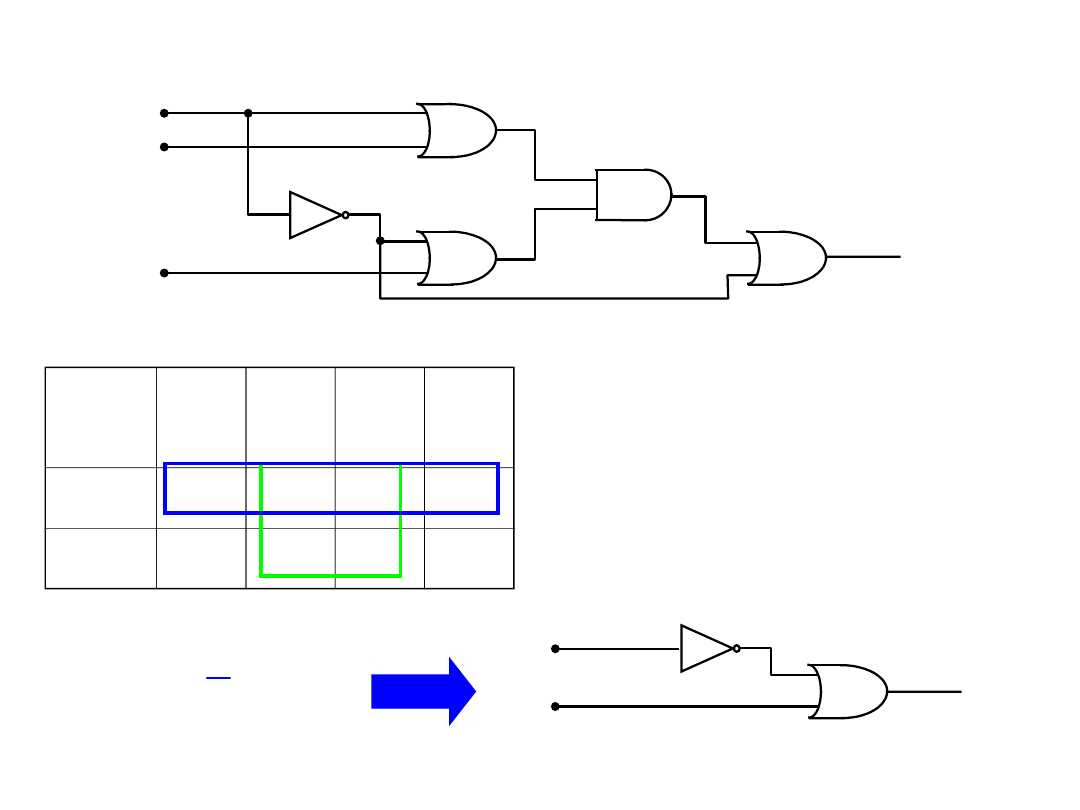
Zjawisko hazardu dynamicznego

=

=

2

3

0

x

x

1

x

F

1

F

2

F

3

F

F

4

0

1

t

t

0

1

1

0

t

0

1

1

0

1

t

0

1

0

t

Hazard

dynamiczny

1

0

0

1

1

0

0

t

0

1

0

1

0

0

1

0

1

0

1

1

0

t

1

0

0

1

0

1

14

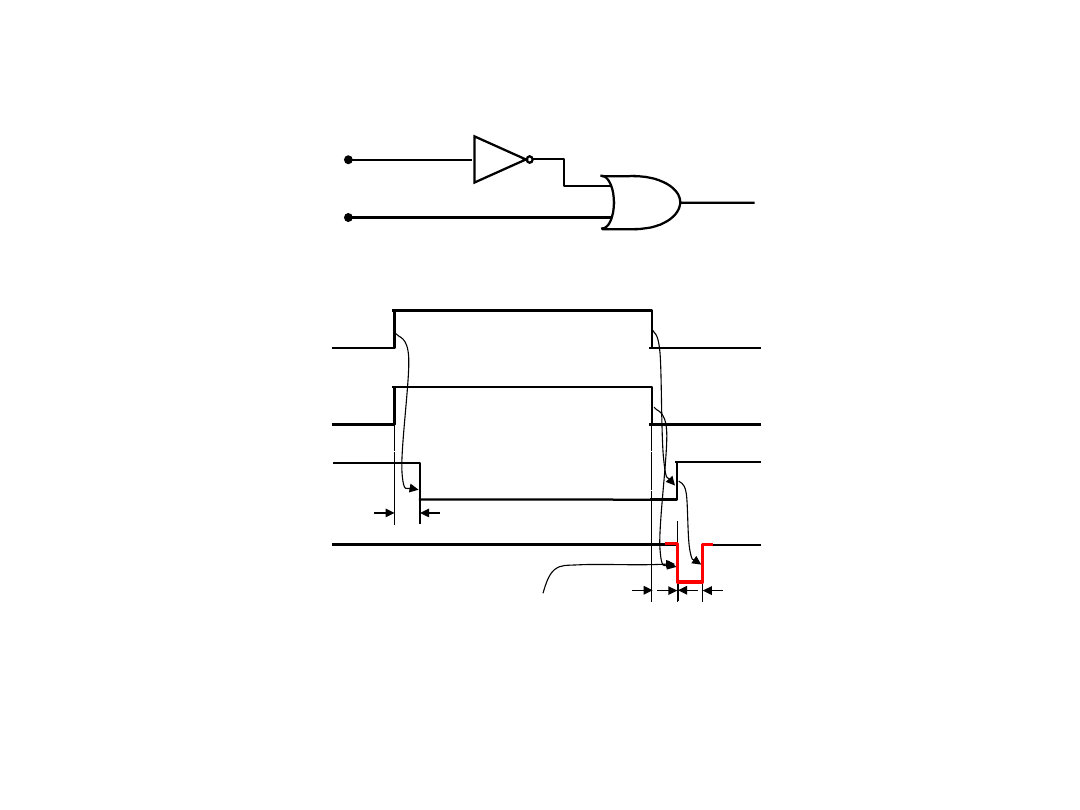
Zjawisko hazardu dynamicznego

F

3

x

2

x

1

x

F

1

F

2

F

4

F

3

x

2

x

3

x

1

00

01

11

10

0

1

1

1

1

1

1

1

1

F

x

=

3

x

+

F

3

x

1

x

F

1

15

t

0

0

Zjawisko hazardu dynamicznego

F

3

x

1

x

F

1

1

x

F

1

F

3

x

1

1

1

0

0

1

0

1

1

1

0

1

0

1

0

t

t

0

0

0

1

1

0

1

0

1

Hazard statyczny

w 1

16

0

1

0

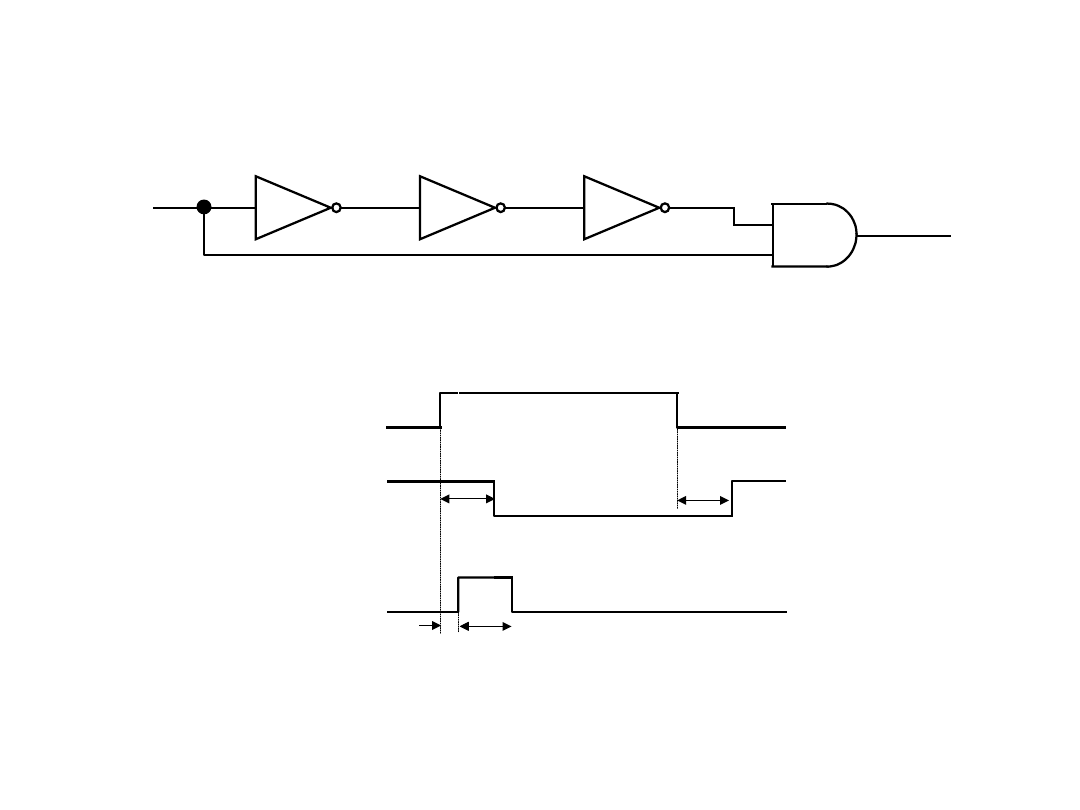
Detektor narastającego zbocza sygnału

x

F

t

3

t

t

t

t

1

x

F

1

F

1

F

t

1

t

3

1

0

t

3

0

1

0

1

0

1

1

0

1

0

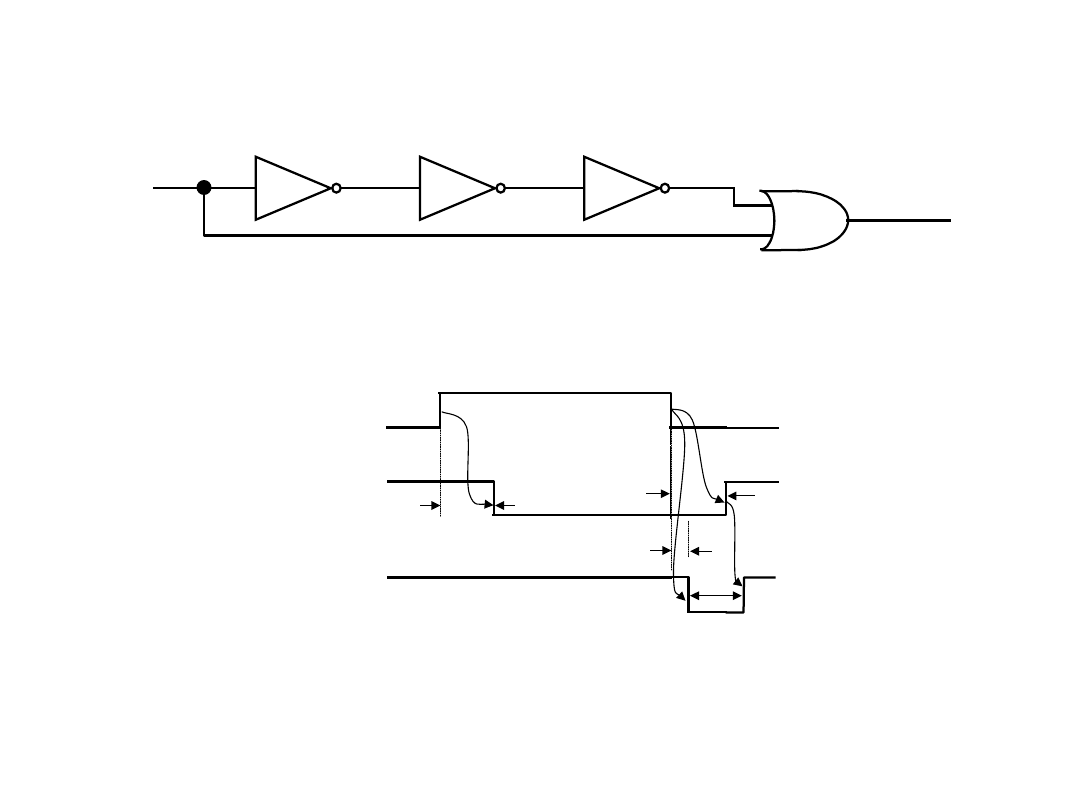
17

1

0

0

1

Detektor opadającego zbocza sygnału

x

F

1

F

x

F

t

t

t

t

1

F

1

t

3

1

t

3

1

0

t

1

1

0

0

1

0

0

1

0

t

3

1

0

1

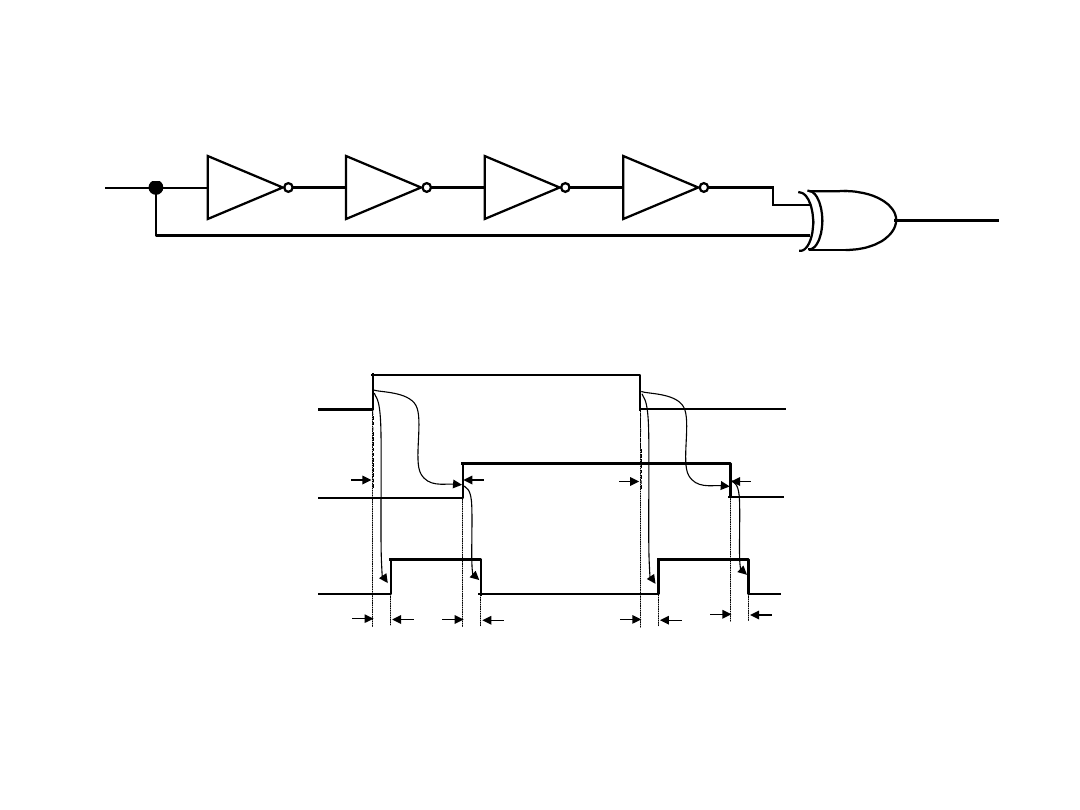
18

Detektor opadającego zbocza sygnału

x

F

1

F

t

1

0

0

0

x

F

t

t

t

t

1

F

1

t

0

1

0

1

1

t

4

0

1

1

t

1

1

1

0

1

0

0

t

1

0

0

1

t

4

1

1

0

t

1

0

1

0

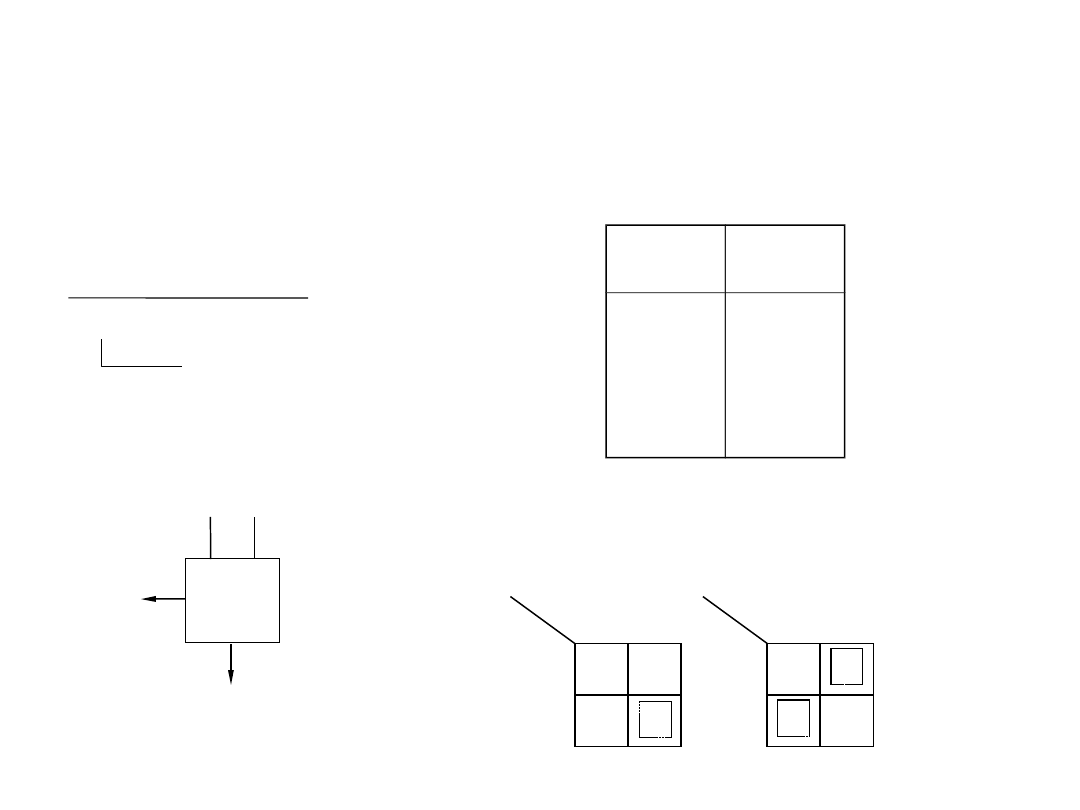
19

Układy arytmetyczne

Układ półsumatora

A
B

C
S

Czynniki

Suma
Przeniesieni
e

A

C

B

S



Równanie

Symbol

Tabela

prawdy

A B S C

0 0
0 1
1 0
1 1

0 0
1 0
1 0
0 1

0

1

0

0

0

1

0

1

A

B

C

1

0

1

0

0

1

0

1

A

B

S

Tablice

Karnaugha

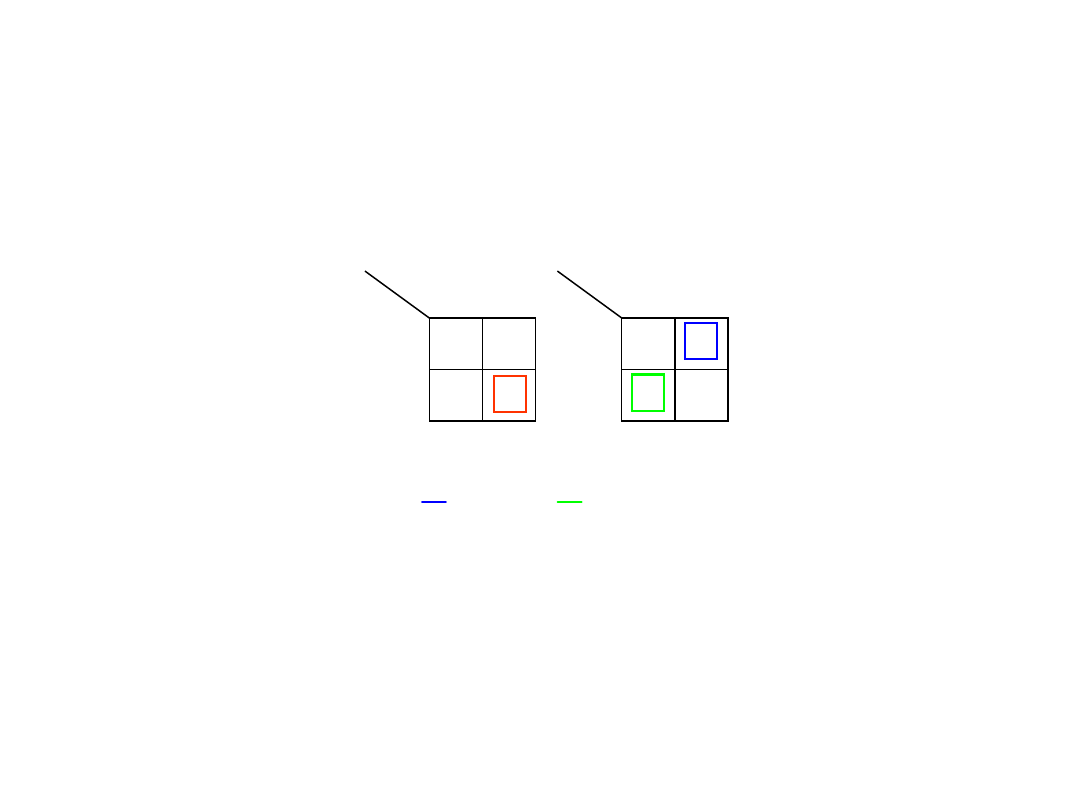
20

Układy arytmetyczne

Układ półsumatora

0

1

0

0

0

1

0

1

A

B

C

1

0

1

0

0

1

0

1

A

B

S

Tablice

Karnaugha

S

AB

=

A B

= �

=

C

AB

AB

+

21

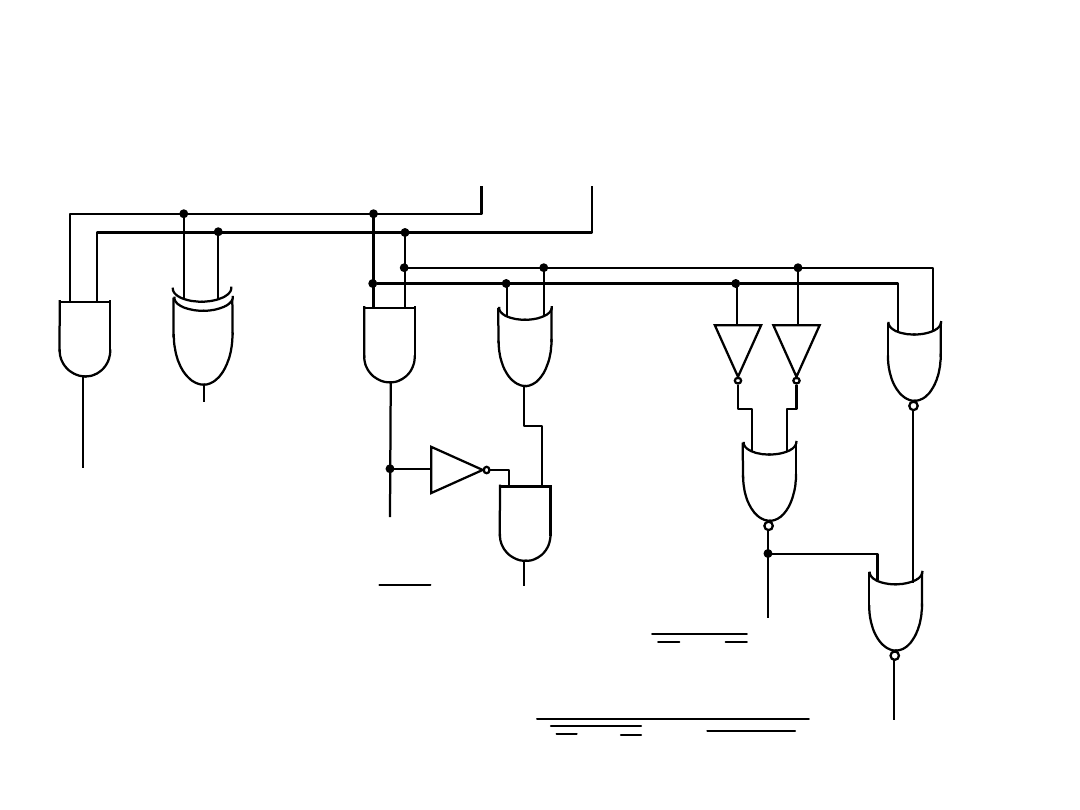
Układy arytmetyczne

Przykłady implementacji układowej

półsumatora

B

A

S A B

= �

C AB

=

(

)

S

A B AB A B

= +

= �

C AB

=

(

)

C

A B

AB

= +

=

(

) (

)

S

A B

A B

A B

= + + + = �

Przykład

22

00

01

11

10

0

0

1

0

1

1

1

0

1

0

00

01

11

10

0

0

0

1

0

1

0

1

1

1

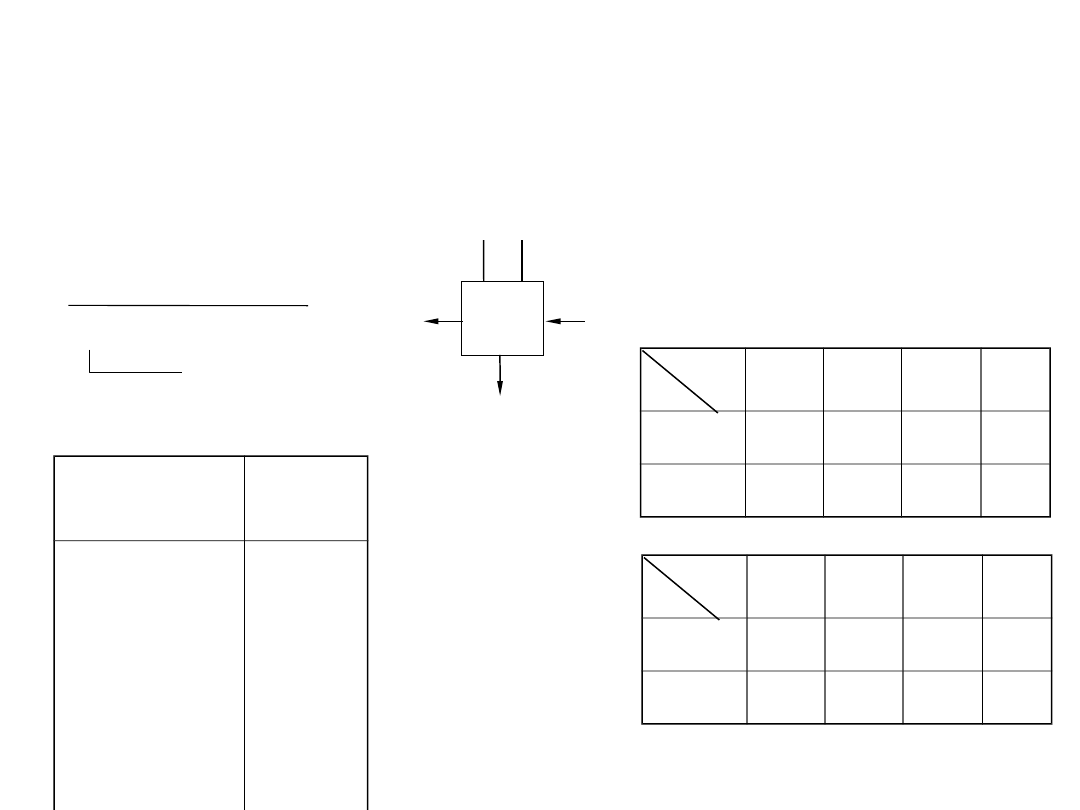
Układy arytmetyczne

Układ sumatora

A

i

B

i

C

i-1

C

i

S

i

Czynniki

Suma
Przeniesieni
e

Równanie

Symbol

Tabela

prawdy

A

i

B

i

C

i-1

S

i

C

i

0 0 0

0 0 1

0 1 0

0 1 1

1 0 0

1 0 1

1 1 0

1 1 1

0 0

1 0

1 0

0 1

1 0

0 1

0 1

1 1

Tablice

Karnaugha

C

i

A

i

B

i

C

i-1

S

i

A

i

B

i

C

i-1

A

i

C

i

B

i

S

i



C

i-1

ZAOCZNE

23

00

01

11

10

0

0

1

0

1

1

1

0

1

0

00

01

11

10

0

0

0

1

0

1

0

1

1

1

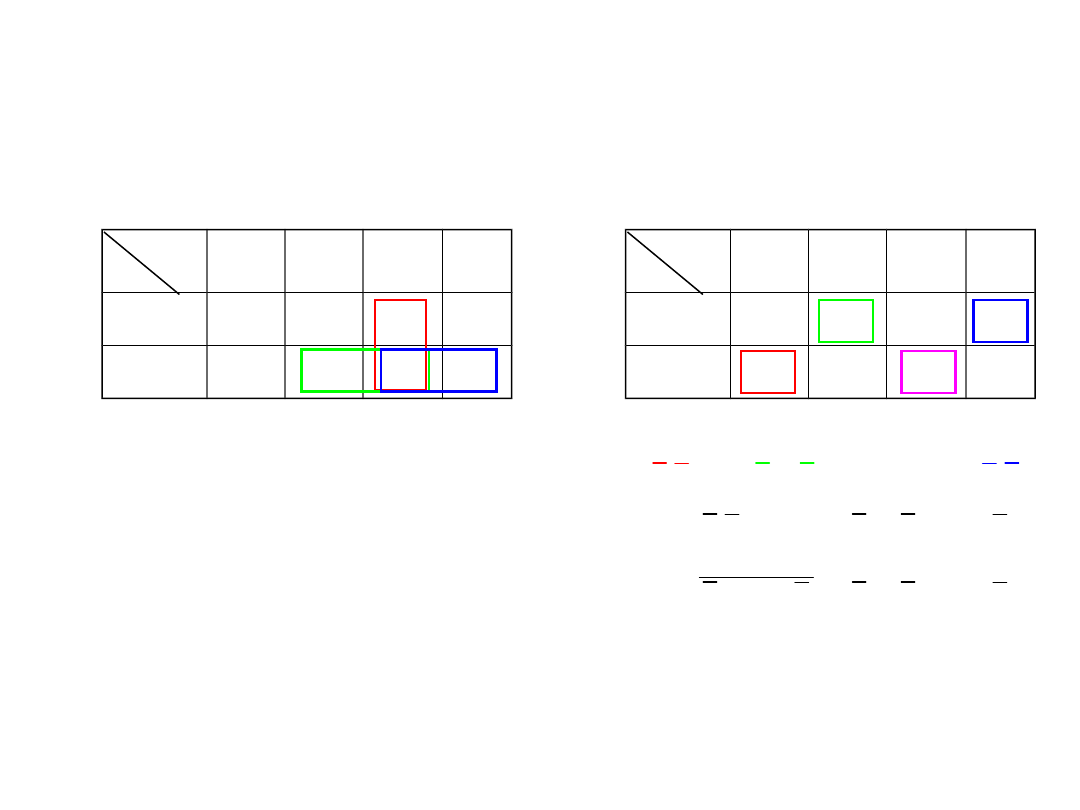
Układy arytmetyczne

Układ sumatora

Tablice

Karnaugha

C

i

A

i

B

i

C

i-1

S

i

A

i

B

i

C

i-1

1

i

i

i

i

ABC

S

-

=

1

i i i

ABC

-

+

1

i i i

ABC

-

+

1

i i

i

ABC

-

+

1

1

(

)

(

)

i

i i

i i

i

i i

i

C

AB AB

C

AB AB

-

-

=

+

+

+

=

1

i

i

i

A

B

C

-

= � �

i

i

i

C

AB

=

1

i i

BC

-

+

1

i

i

AC

-

+

1

(

)

i i

i

i

i

AB C

A

B

-

=

+

�

1

(

)

i i

i

i

i

AB C

A B

-

=

+

+

=

=

1

1

(

)

(

)

i

i i

i i

i

i i

i

C

AB AB

C

AB AB

-

-

=

+

+

+

=

=

24

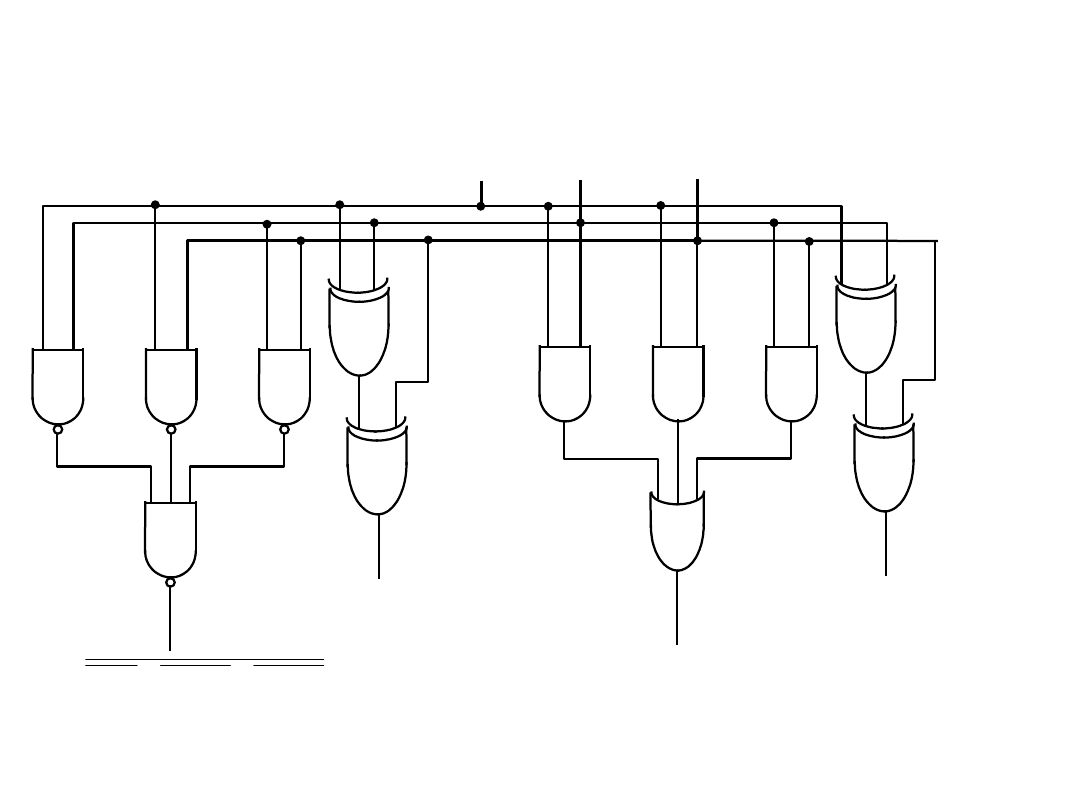
Układy arytmetyczne

Przykłady implementacji układowej sumatora

B

i

A

i

C

i-

1

1

i

i

i

i

S

A

B

C

-

= � �

1

1

*

*

i

i i

i i

i i

C

AB AC

BC

-

-

=

1

1

i i

i

i

i i

AB AC

BC

-

-

=

+

+

=

1

i

i

i

i

S

A

B

C

-

= � �

1

1

i

i i

i

i

i i

C

AB AC

BC

-

-

=

+

+

Przykład

25

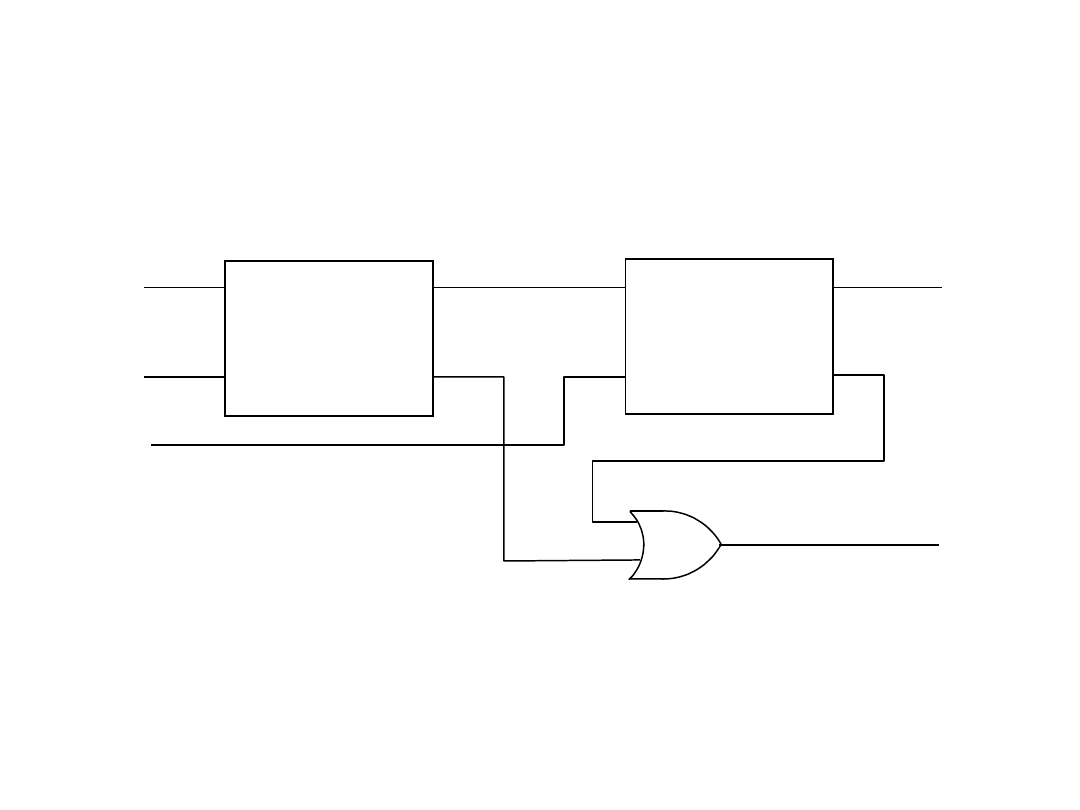
Układy arytmetyczne

Realizacja układ sumatora z dwóch

półsumatorów

A

i

B

i

PÓŁSUMATOR

PÓŁSUMATOR

AB

S

i

C

i

C

i-1

Przykład

26

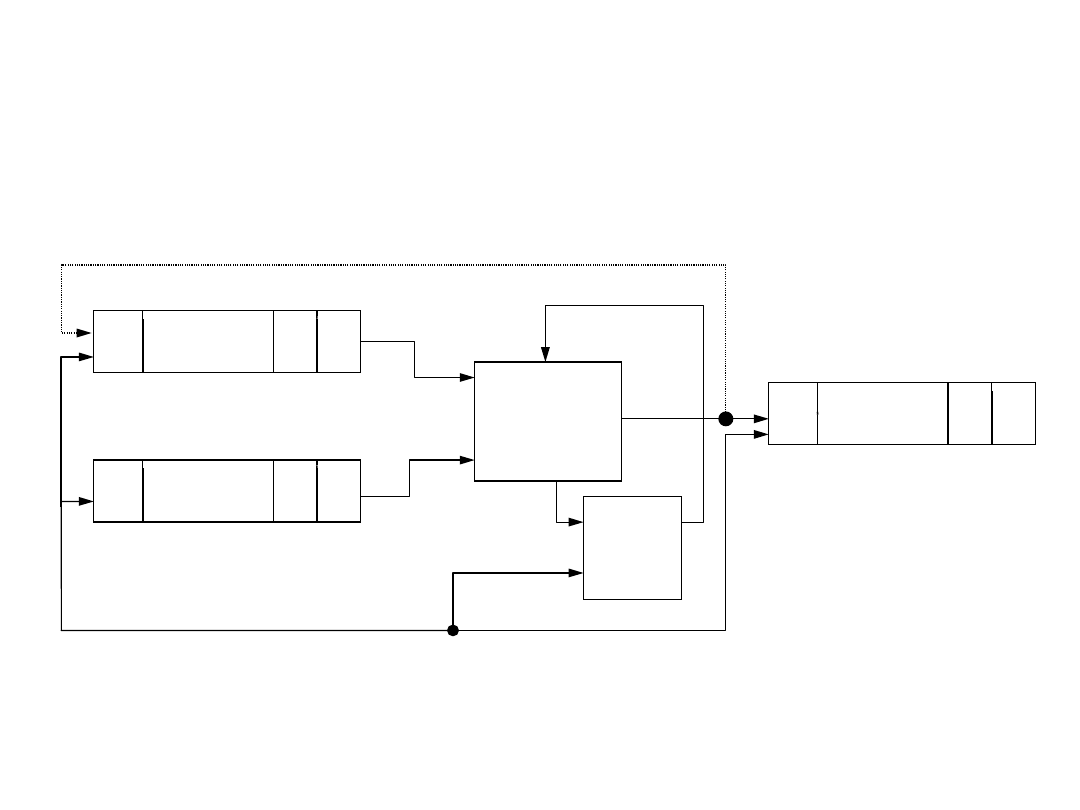
Układy arytmetyczne

Sumator wielobitowy szeregowy

A C

i-1

S

B
C

i

D
Q

C

........

........

Składnik A

Zegar

n-bitowy rejestr

przesuwający

n-bitowy rejestr

przesuwający

........

Suma

n-bitowy rejestr

przesuwający

Składnik B

27

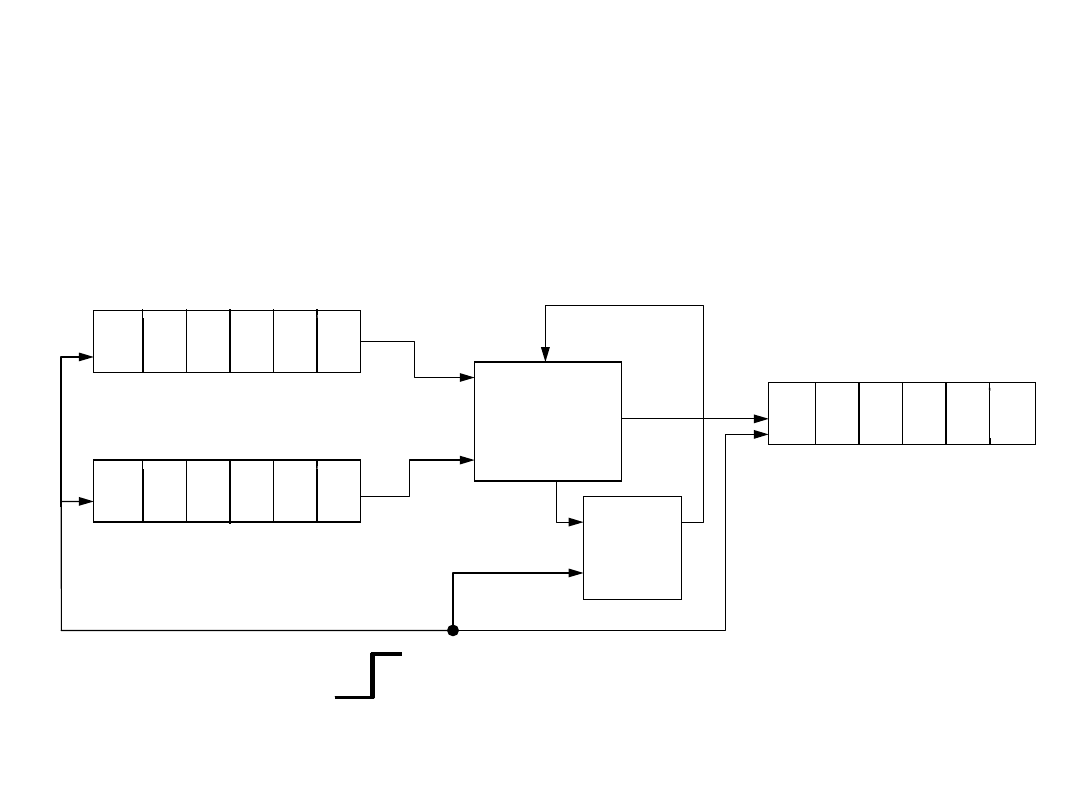
Układy arytmetyczne

Sumator wielobitowy szeregowy

A C

i-1

S

B
C

i

D
Q

C

Składnik A

Zegar

6-bitowy rejestr

przesuwający

6-bitowy rejestr

przesuwający

Suma

6-bitowy rejestr

przesuwający

Składnik B

0 0 0 1 0 1

1 0 1 0 0 1

0 0 0 0 0 0

0

0

1

1

0 0 0 0 1 0

0 1 0 1 0 0

0

1

0

0 0 1 0 1 0

0 0 0 0 0 1

1 0 0 0 0 0

0

1

0

1 1 0 0 0 0

0 0 0 0 0 0

0 0 0 1 0 1

0

1

2

3

0

1

4

0

0 0 0 0 1 0

1 1 1 0 0 0

0

0

5

0

0 1 1 1 0 0

0 0 0 0 0 1

0

1

6

0

1 0 1 1 1 0

0 0 0 0 0 0

0

0

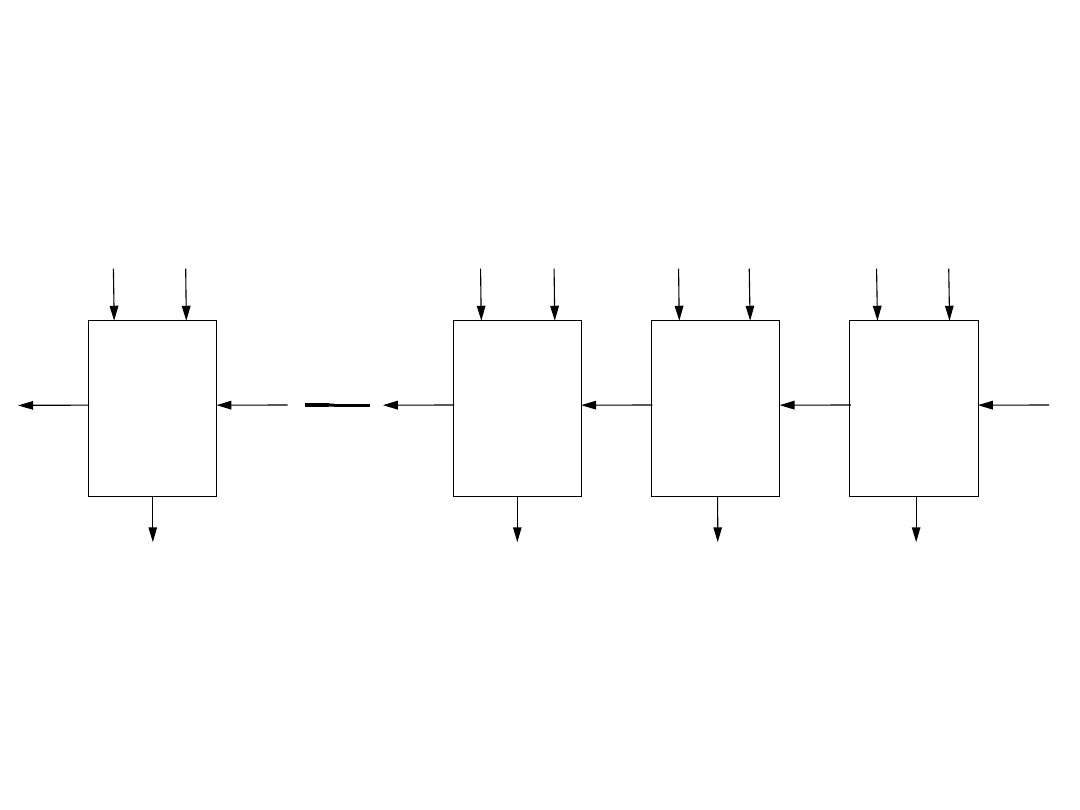
28

Układy arytmetyczne

Sumator wielobitowy równoległy z przeniesieniami

szeregowymi

B A

C

i

C

i-

1

S

A

1

B

1

C

0

S

1

B A

C

i

C

i-1

S

A

2

B

2

C

1

S

2

B A

C

i

C

i-

1

S

A

3

B

3

C

2

S

3

B A

C

i

C

i-1

S

A

n

B

n

C

n-1

S

n

C

n

C

3









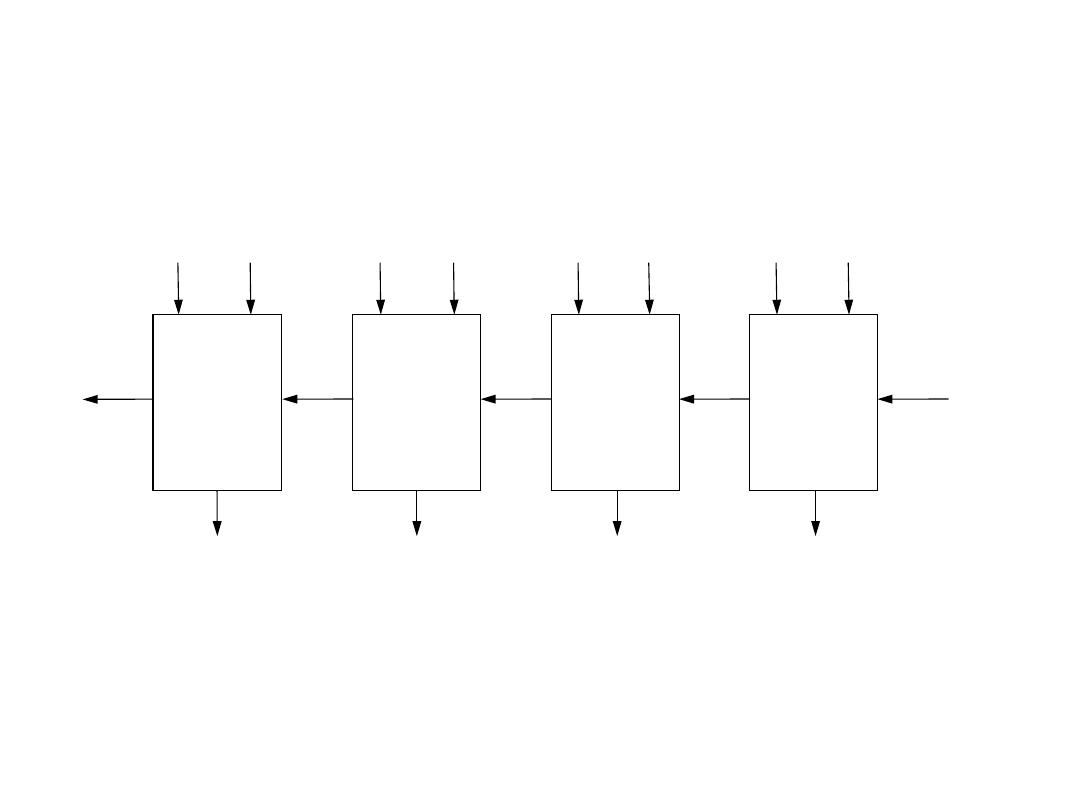
29

Układy arytmetyczne

Sumator wielobitowy równoległy z przeniesieniami

szeregowymi

B A

C

i

C

i-

1

S

B A

C

i

C

i-1

S

A

1

B

1

C

0

S

1

A

2

B

2

C

1

S

2

B A

C

i

C

i-

1

S

A

3

B

3

C

2

S

3

B A

C

i

C

i-1

S

A

4

B

4

S

4

C

5

C

3









0

1

1

1

0

1

1

1

1

0

1

0

1

0

1

0

1

30

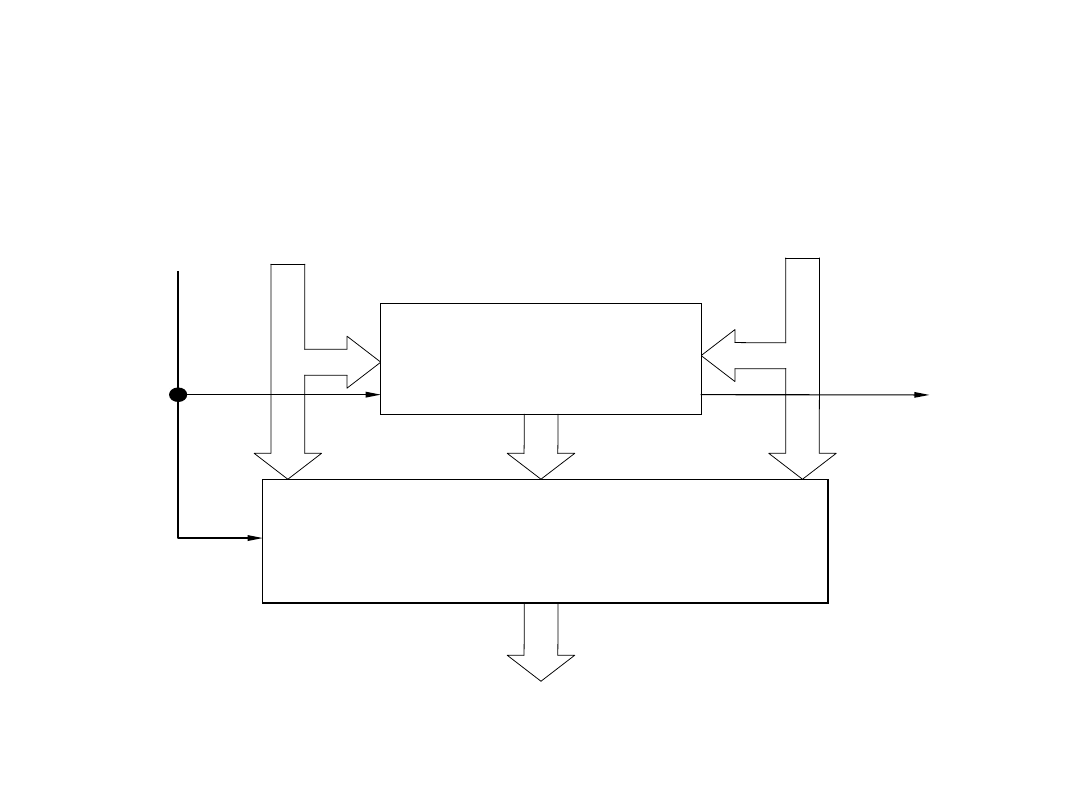
Układy arytmetyczne

Sumator wielobitowy równoległy z przeniesieniami

jednoczesnymi

Blok

przeniesień

Blok sumy

A

B

S

C

n

C

0

31

Układy arytmetyczne

7483

A1

10

A2

8

A3

3

A4

1

B1

11

B2

7

B3

4

B4

16

C0

13

S1

9

S2

6

S3

2

S4

15

C4

14

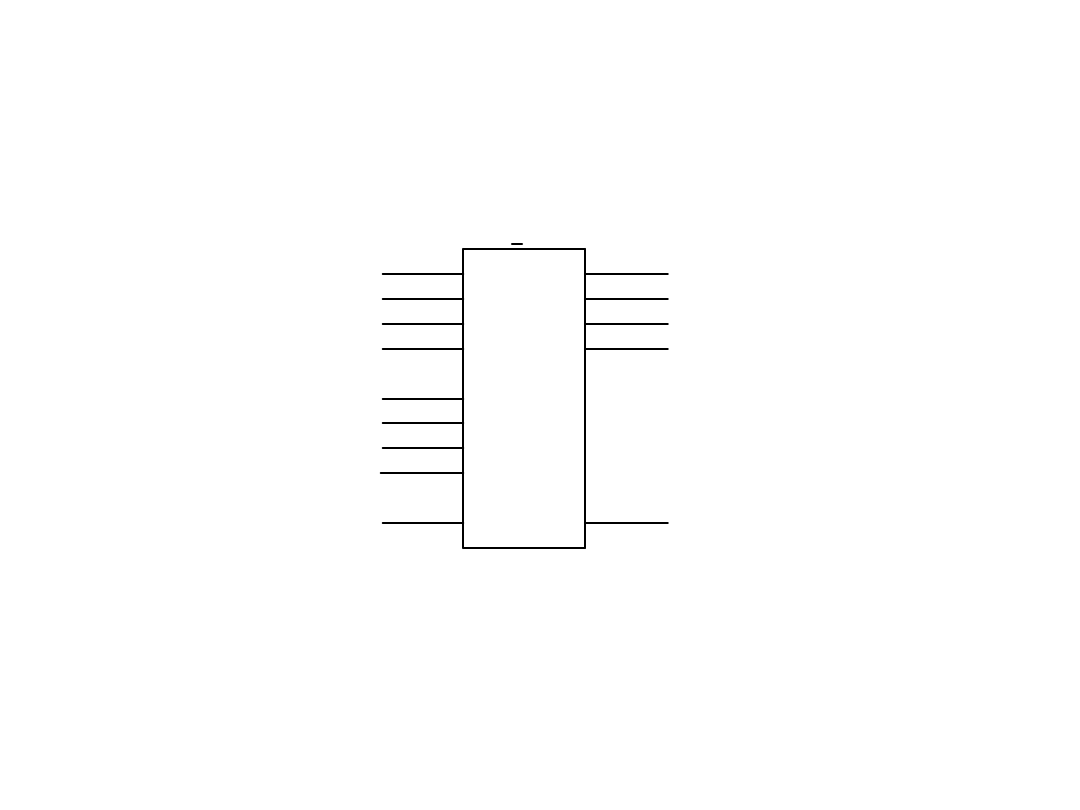
Scalony układ arytmetyczny

32

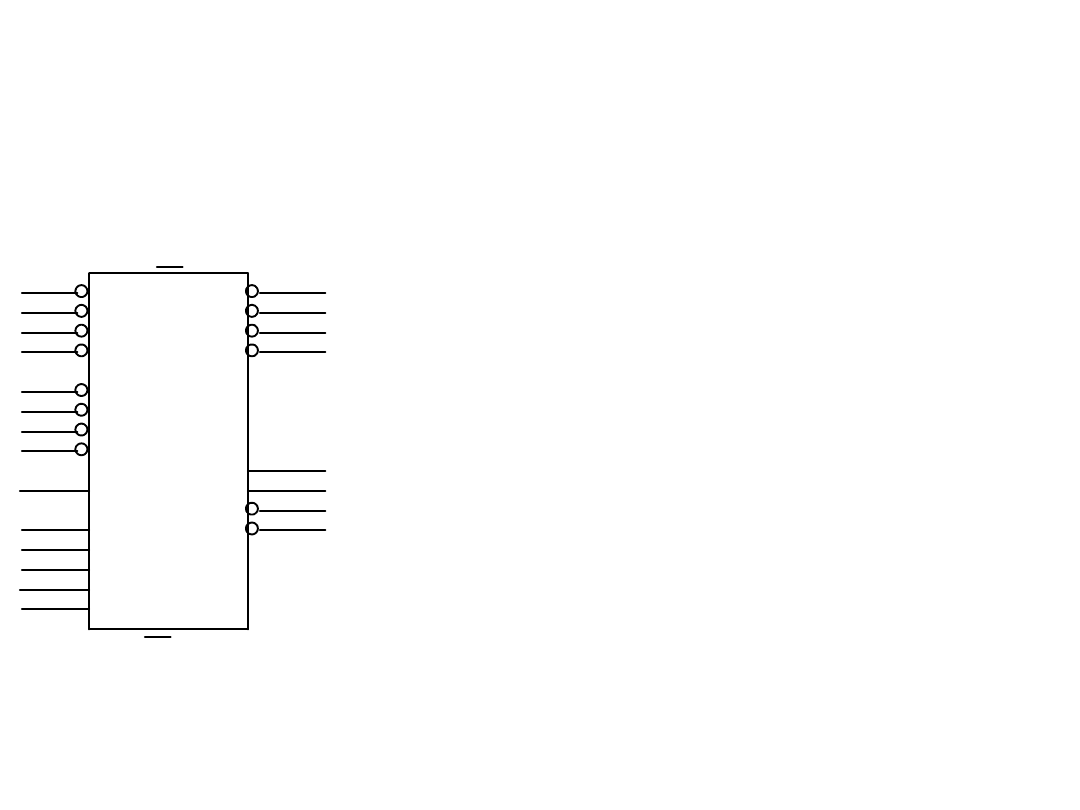
Układy arytmetyczne

Jednostka arytmetyczno-logiczna

74181

A0

2

A1

23

A2

21

A3

19

B0

1

B1

22

B2

20

B3

18

CN

7

S0

6

S1

5

S2

4

S3

3

M

8

F0

9

F1

10

F2

11

F3

13

A=B

14

CN+4

16

G

17

P

15

A0,...,A3 i B0,...,B3 - wejścia dla dwóch słów czterobitowych

C

n

- wejście przeniesienia

M - wejście określające tryb pracy

S

0

,...,S

3

- wejścia wyboru funkcji

F

0

,...,F

3

- wyjście wyniku

C

n+4

- wyjście przeniesienia

G - wyjście przeniesienia generowanego

P - wyjście przeniesienia propagowanego

A = B - wyjście komparacyjne

33

Układy arytmetyczne

Realizacja operacji porównania

A=B

jest w stanie wysokim gdy obydwie liczby są równe

A=B

jest w stanie niskim gdy obydwie liczby są różne

C

A B jeśli f A B

i C

A B jeśli f A B

i C

A B jeśli f A B

i C

n

n

n

n










































0

0

0

1

0

0

1

4

4

4

(

)

(

)

(

)

W wyniku operacji porównania na wyjściach A=B i Cn+4 otrzymujemy:

C

A B jeśli f A B

i C

A B jeśli f A B

i C

A B jeśli f A B

i C

n

n

n

n










































1

0

0

1

1

0

1

4

4

4

(

)

(

)

(

)

34

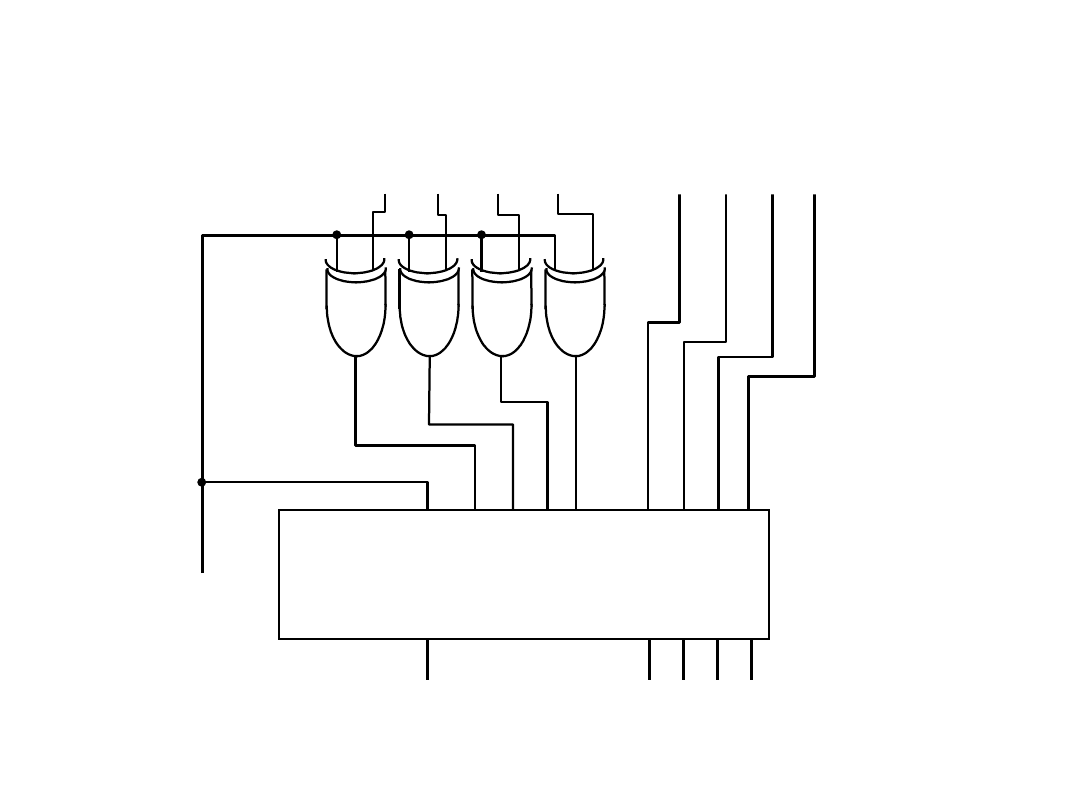
Układ realizujący operację dodawania i

odejmowania

A

4

A

3

A

2

A

1

B

4

B

3

B

2

B

1

Sterowani

e

A

1

S

1

A

2

S

2

A

3

S

3

A

4

S

4

B

1

B

2

B

3

B

4

C

0

C

4

0

0

1

1

0

1

1 0

0

0

1 1

0

1

1 0

0

1

0 1

1

Dodawanie

0

Odejmowa

nie

1

0

1

1

0

1

1 0

0

1

1 0

0

1

0 0

1

0

1 1

1

0

35

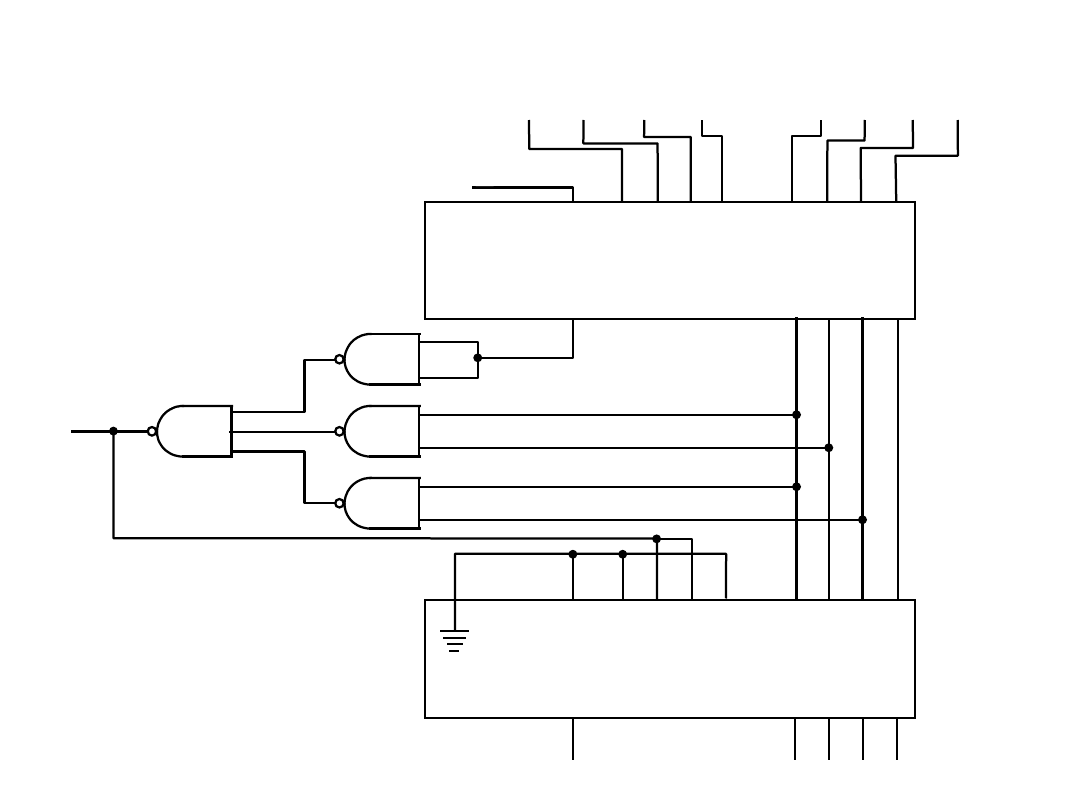
Układ realizujący operację dodawania liczb w

kodzie BCD

A

4

A

3

A

2

A

1

B

4

B

3

B

2

B

1

A

1

S

1

A

2

S

2

A

3

S

3

A

4

S

4

B

1

B

2

B

3

B

4

C

0

C

4

A

1

S

1

A

2

S

2

A

3

S

3

A

4

S

4

B

1

B

2

B

3

B

4

C

0

C

4

C

n

C

n-1

1

1 0

0

1

1 1

0

0

0

1 0

1

0

1

0

1

1

0

1 0

1

0

1 1

0

1

0

0 1

0

36

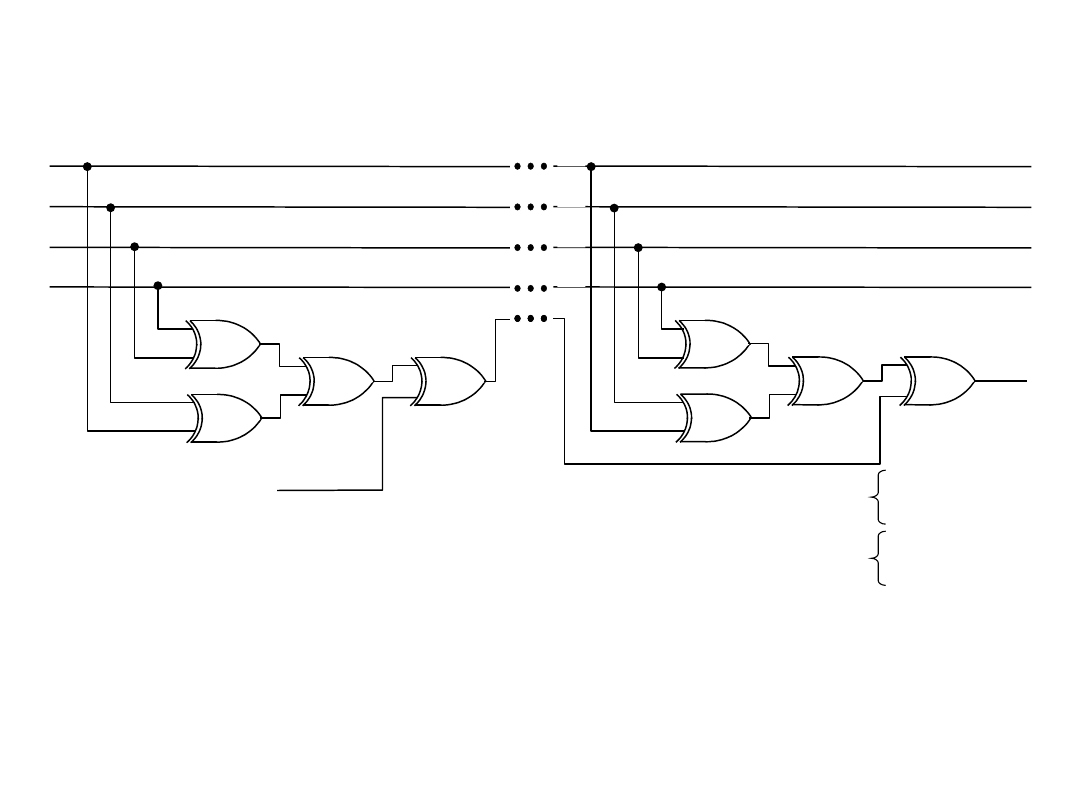
Układ generacji bitu parzystości

Generowanie bitu parzystości polega na wytworzeniu jednego

bitu
i dodaniu go do słowa kodowego, będącego nośnikiem informacji.
Bit ten jest zwany

bitem parzystości.

Jeśli dane słowo kodowe zawiera nieparzystą (parzystą) liczbę

jedynek, to bit parzystości przyjmuje wartość

1

w przeciwnym

przypadku wartość

0

.

Bit parzystości generowany jest zgodnie z równaniem:

0

1

n

A

A

A

�

�

�

K

gdzie:

i

A

- bit słowa informacyjnego (i=0…n).

37

Układ generacji bitu parzystości

Sygnał sterujący:
0 – generacja bitu parzystości;
1 – generacja bitu
nieparzystości.

0 – bez
błędu;
1 – błąd.

A

0

A

1

A

2

A

3

0 – błąd;
1 – bez
błędu.

dla bitu parzystości

dla bitu nieparzystości

0
1
0
0

0

1

0

1

0
1
0
0

1

0

1

1

0

0
1

1

0

1

1

1

1

1

0

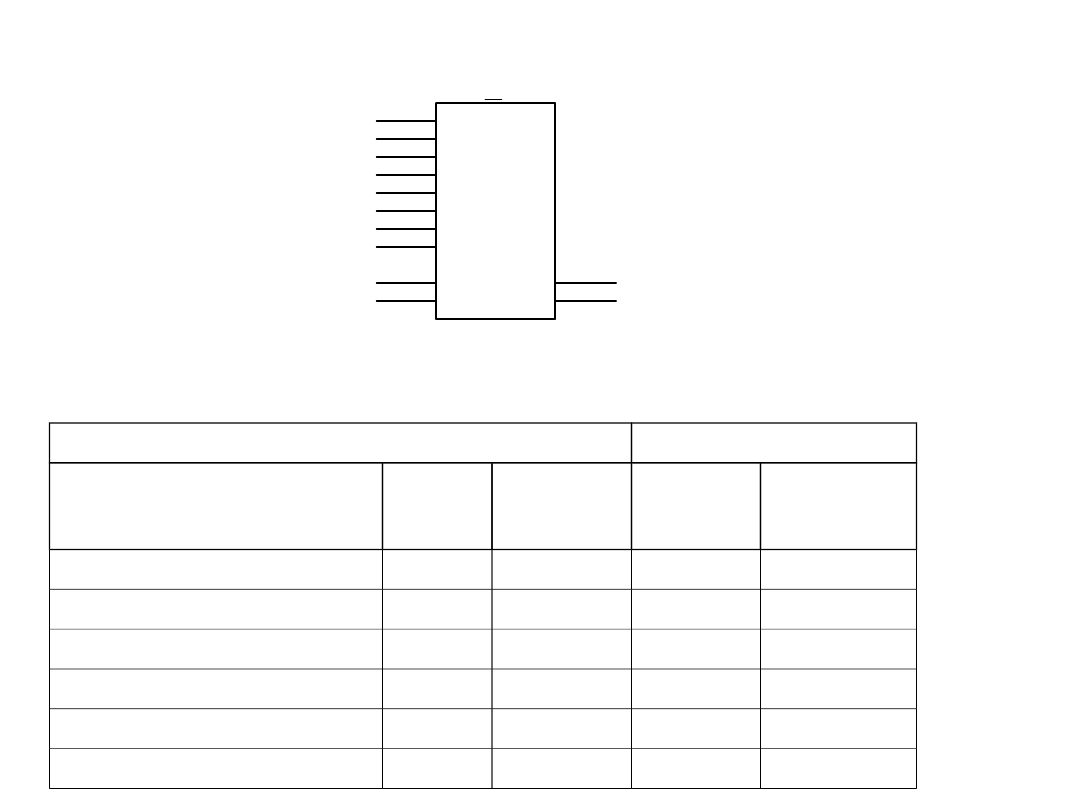
38

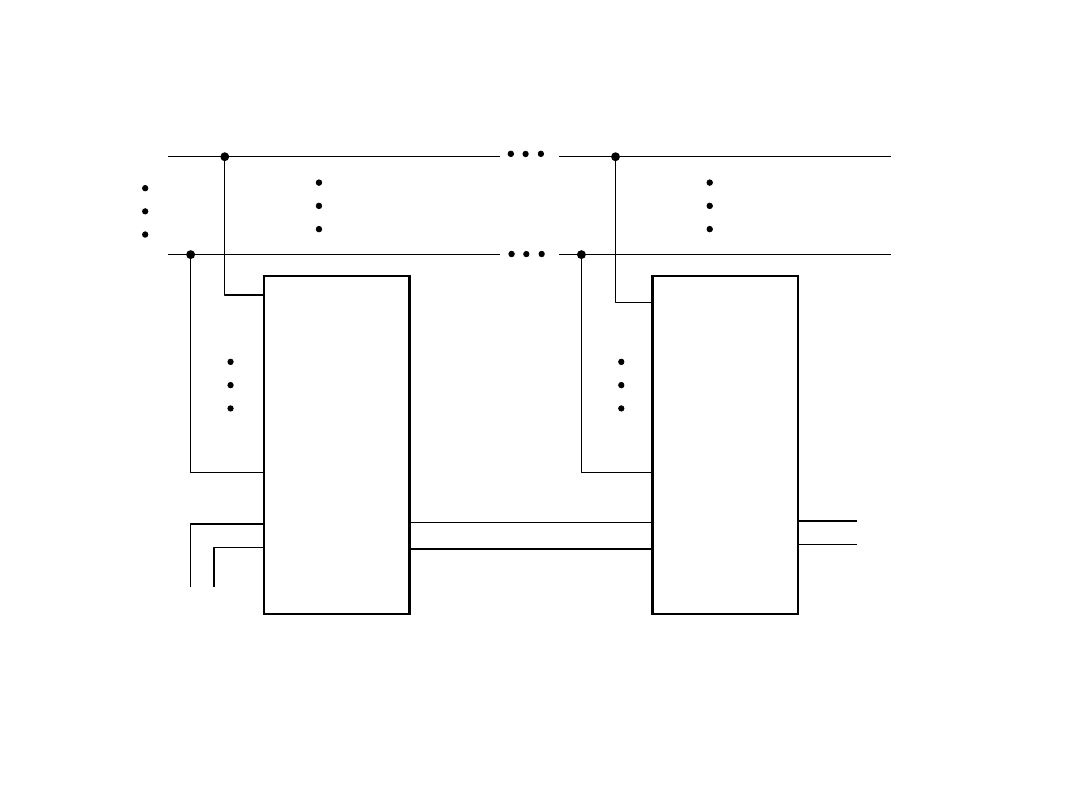
Układ generacji bitu parzystości

74180

A

8

B

9

C

10

D

11

E

12

F

13

G

1

H

2

EI

3

OI

4

EVEN

5

ODD

6

Tabela stanów dla układu 74180

Wejścia

Wyjścia

Liczba stanów 1 na

wejściach danych (A...H)

od 0 do 7 jest:

Parzyst

e (EI)

Nieparzys

te (OI)

Parzyste

(EVEN)

Nieparzyst

e (ODD)

Parzysta

1

0

1

0

Nieparzysta

1

0

0

1

Parzysta

0

1

0

1

Nieparzysta

0

1

1

0

X

1

1

0

0

X

0

0

1

1

39

Układ generacji bitu parzystości

A
B
C
D
E
F
G
H

EI

EVEN

OI
ODD

74

18

0

B

0

B

7

Wejścia sterujące

W

y

jś

c

ia

k

o

n

tr

o

ln

e

A
B
C
D
E
F
G
H

EI

EVEN

OI
ODD

74

18

0

40

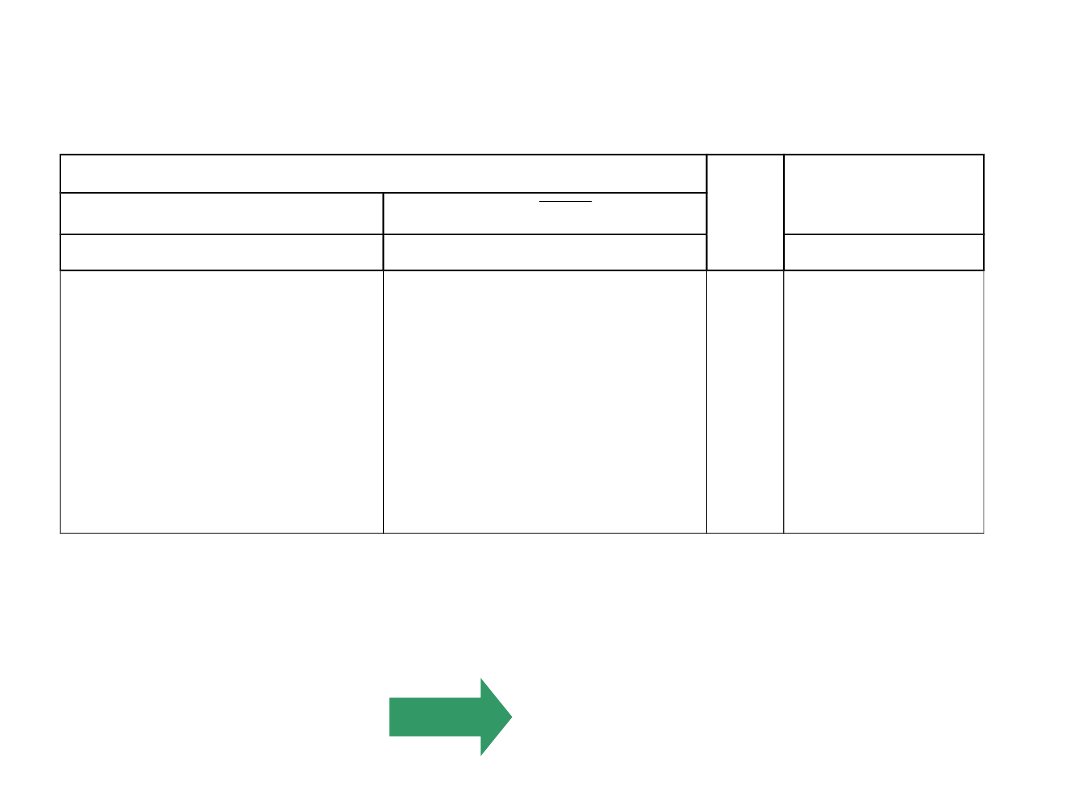
Układy konwersji kodów

Podzia
ł:

•transkodery.

•enkodery (zwane również koderami);

•dekodery;

zwykłe

priorytetowe

pełne - jeżeli 2

n

=

m

niepełne - jeżeli 2

n

<

m

41

Wejścia

Wyjścia

Kod 1 z 10

Kod

9 8 7 6 5 4 3 2 1 0

9 8 7 6 5 4 3 2 1 0

D C B A

0 0 0 0 0 0 0 0 0

1

0 0 0 0 0 0 0 0

1

0

0 0 0 0 0 0 0

1

0 0

0 0 0 0 0 0

1

0 0 0

0 0 0 0 0

1

0 0 0 0

0 0 0 0

1

0 0 0 0 0

0 0 0

1

0 0 0 0 0 0

0 0

1

0 0 0 0 0 0 0

0

1

0 0 0 0 0 0 0 0

1

0 0 0 0 0 0 0 0 0

1 1 1 1 1 1 1 1 1

0

1 1 1 1 1 1 1 1

0

1

1 1 1 1 1 1 1

0

1 1

1 1 1 1 1 1

0

1 1 1

1 1 1 1 1

0

1 1 1 1

1 1 1 1

0

1 1 1 1 1

1 1 1

0

1 1 1 1 1 1

1 1

0

1 1 1 1 1 1 1

1

0

1 1 1 1 1 1 1 1

0

1 1 1 1 1 1 1 1 1

0
1
2
3
4
5
6
7
8
9

0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1

Układ enkodera zwykłego

Tabela

prawdy

1 10

z

A = 1 + 3 + 5 + 7 + 9

B = 2 + 3 + 6 + 7

C = 4 + 5 + 6 + 7

D = 8 + 9

A = (1 + 9) + (3 + 7) + (5 + 7)

B = (2 + 6) + (3 + 7)

C = (4 + 6) + (5 + 7)

D = 8 + 9

Równania dla enkodera 1 z

10

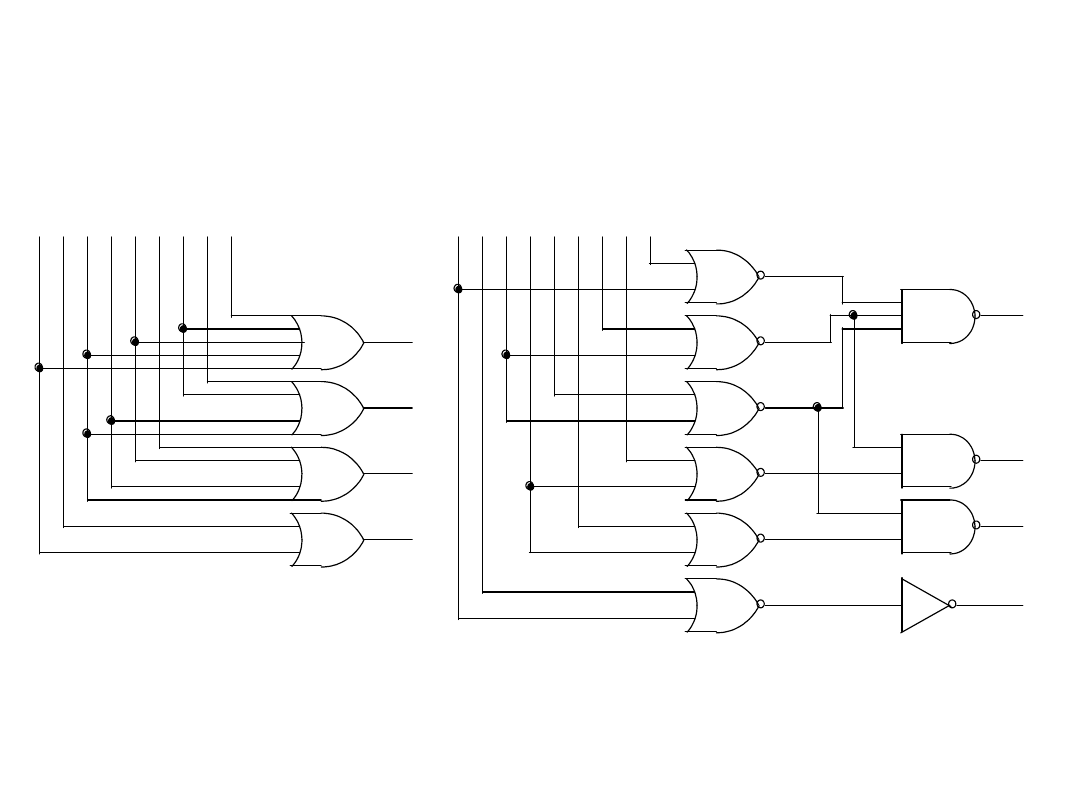
42

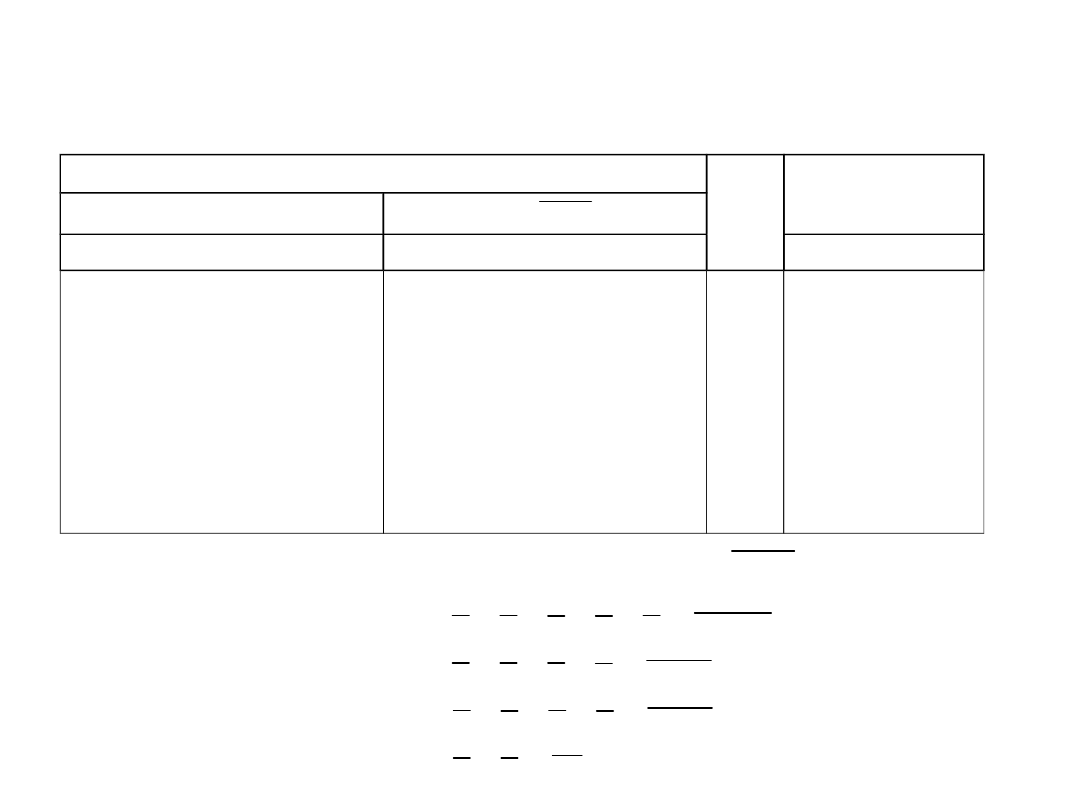
Układ enkodera zwykłego

Realizacje układowe

1

2

3

4

5

6

7

8

9

A

B

C

D

Kod 1 z 10

a)

1

2

3

4

5

6

7

8

9

A

B

C

D

Kod 1 z 10

b)

OR

OR

OR

OR

NOR

NOR

NOR

NOR

NOR

NOR

NAND

AND

AND

NOT

Przykład:
enkoder1z10.msm

43

Wejścia

Wyjścia

Kod 1 z 10

Kod

9 8 7 6 5 4 3 2 1 0

9 8 7 6 5 4 3 2 1 0

D C B A

0 0 0 0 0 0 0 0 0

1

0 0 0 0 0 0 0 0

1

0

0 0 0 0 0 0 0

1

0 0

0 0 0 0 0 0

1

0 0 0

0 0 0 0 0

1

0 0 0 0

0 0 0 0

1

0 0 0 0 0

0 0 0

1

0 0 0 0 0 0

0 0

1

0 0 0 0 0 0 0

0

1

0 0 0 0 0 0 0 0

1

0 0 0 0 0 0 0 0 0

1 1 1 1 1 1 1 1 1

0

1 1 1 1 1 1 1 1

0

1

1 1 1 1 1 1 1

0

1 1

1 1 1 1 1 1

0

1 1 1

1 1 1 1 1

0

1 1 1 1

1 1 1 1

0

1 1 1 1 1

1 1 1

0

1 1 1 1 1 1

1 1

0

1 1 1 1 1 1 1

1

0

1 1 1 1 1 1 1 1

0

1 1 1 1 1 1 1 1 1

0
1
2
3
4
5
6
7
8
9

0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1

Układ enkodera zwykłego

Tabela

prawdy

1 10

z

Równania dla enkodera

1 10

z

1 3 5 7 9 13579

A= + + + + =

2 3 6 7 2367

= + + + =

B

4 5 6 7 4567

= + + + =

C

8 9 89

= + =

D

44

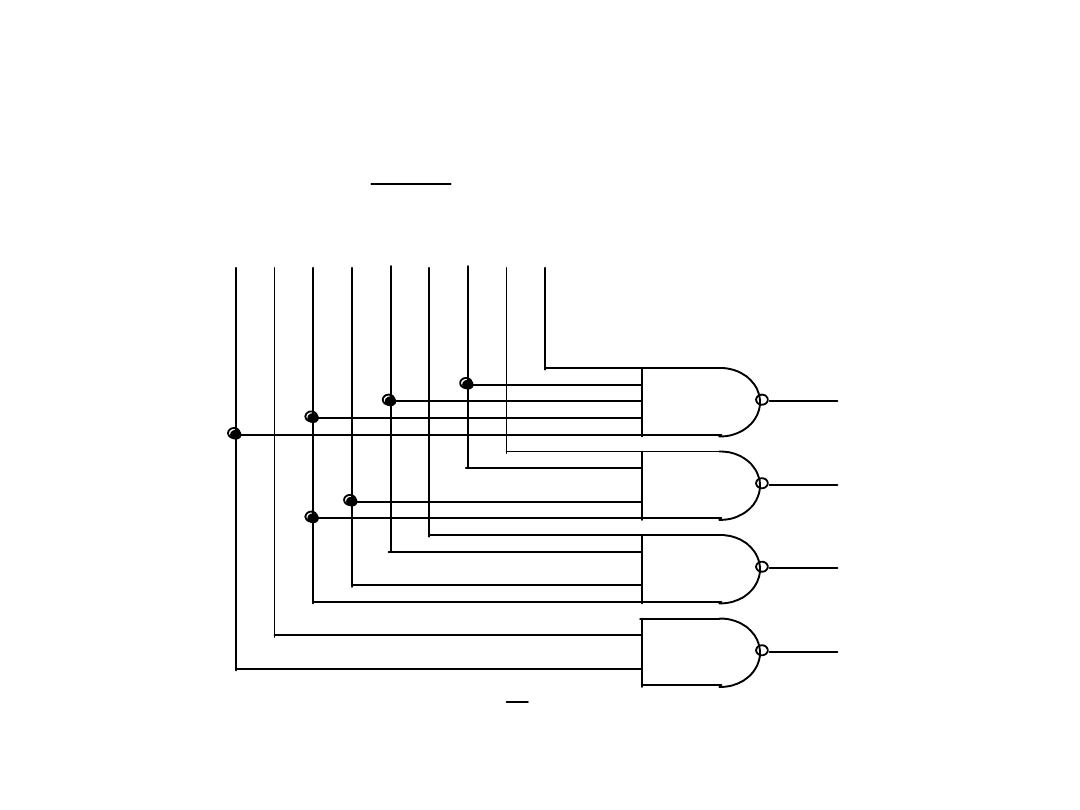
Układ enkodera zwykłego

Realizacje układowe

Przykład:
enkoder_nie_1z10.msm

Kod 1 z 10

9

D

B

4

8

A

3 2

C

1

6

a)

7

5

NAND

NAND

NAND

NAND

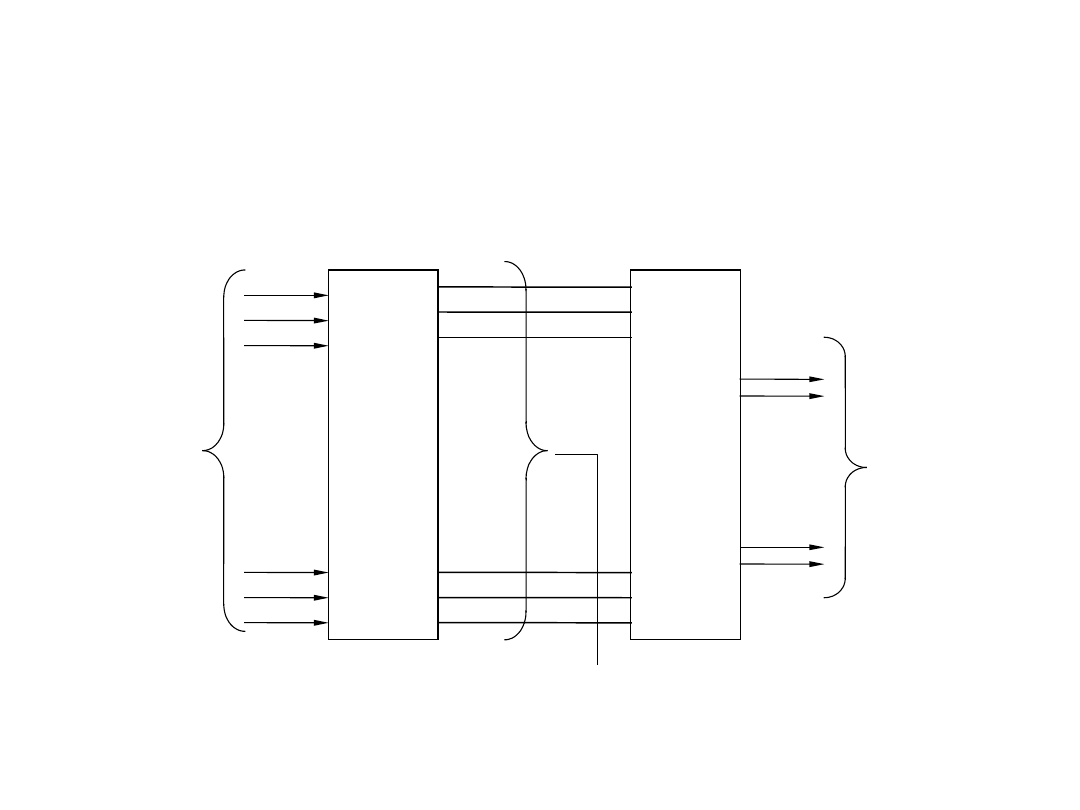
45

Układ enkodera priorytetowego

Kod 1 z n

.
.
.
.

.
.
.
.

K

o
d

x

z

n

K

o
d

w

y

j

ś
c

i

o

w

y

Realizacja z konwersją

pośrednią

46

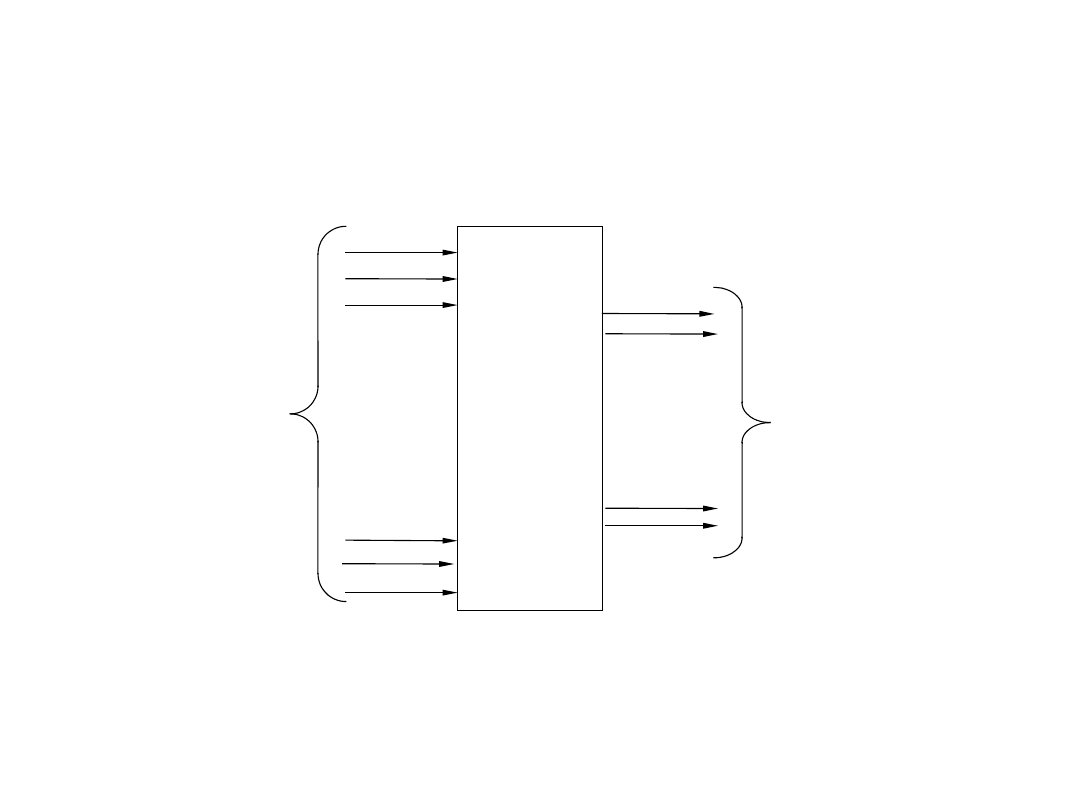
Układ enkodera priorytetowego

Realizacja z konwersją

bezpośrednią

.
.
.
.

.
.
.
.

K

o
d

x

z

n

K

o
d

w

y

j

ś
c

i

o

w

y

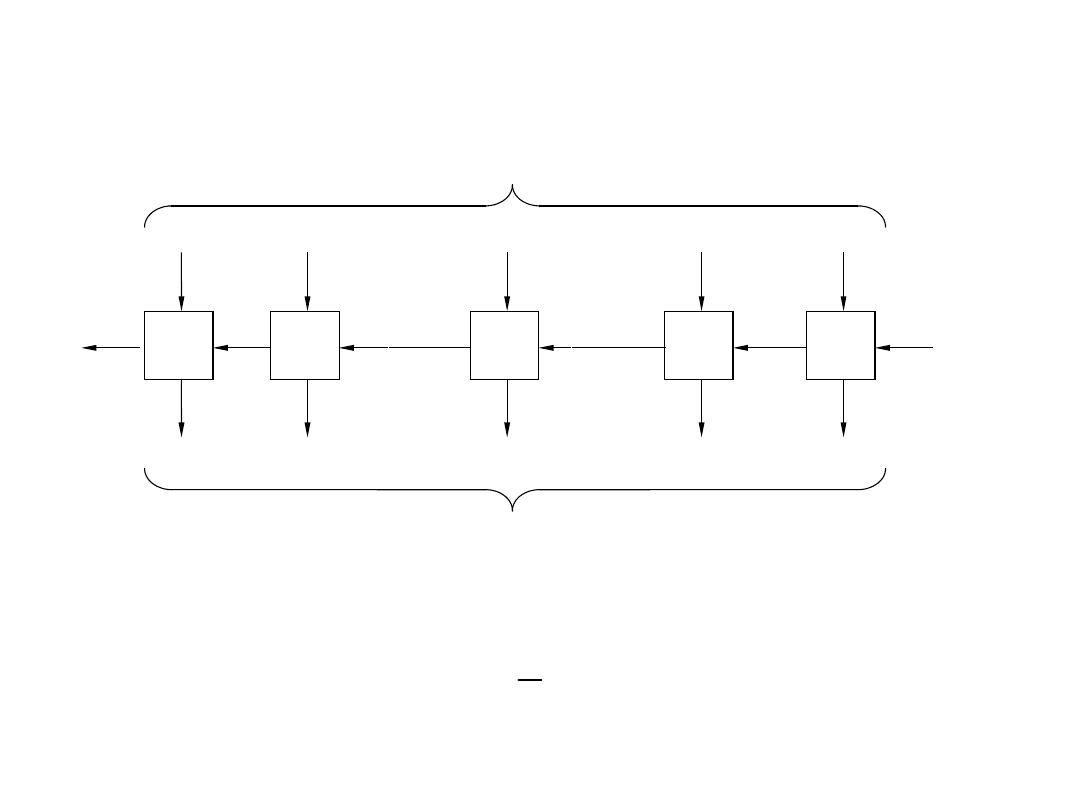
47

Układ enkodera priorytetowego

Realizacja iteracyjna konwersji kodu x z n na

kod 1 z n

x z

n

n - 1

Y

n-1

B

n

E

n-1

n - 2

Y

n-2

B

n-1

E

n-2

B

n-2

B

i+1

i

Y

i-1

B

2

E

i-1

1

Y

1

B

1

E

1

0

Y

0

B

0

E

0

B

i

1 z

n

Funkcje przełączające i-tego stopnia mają postać:

B

B

E

i

i

i





1

1

*

i

i

i

Y B

E

+

=

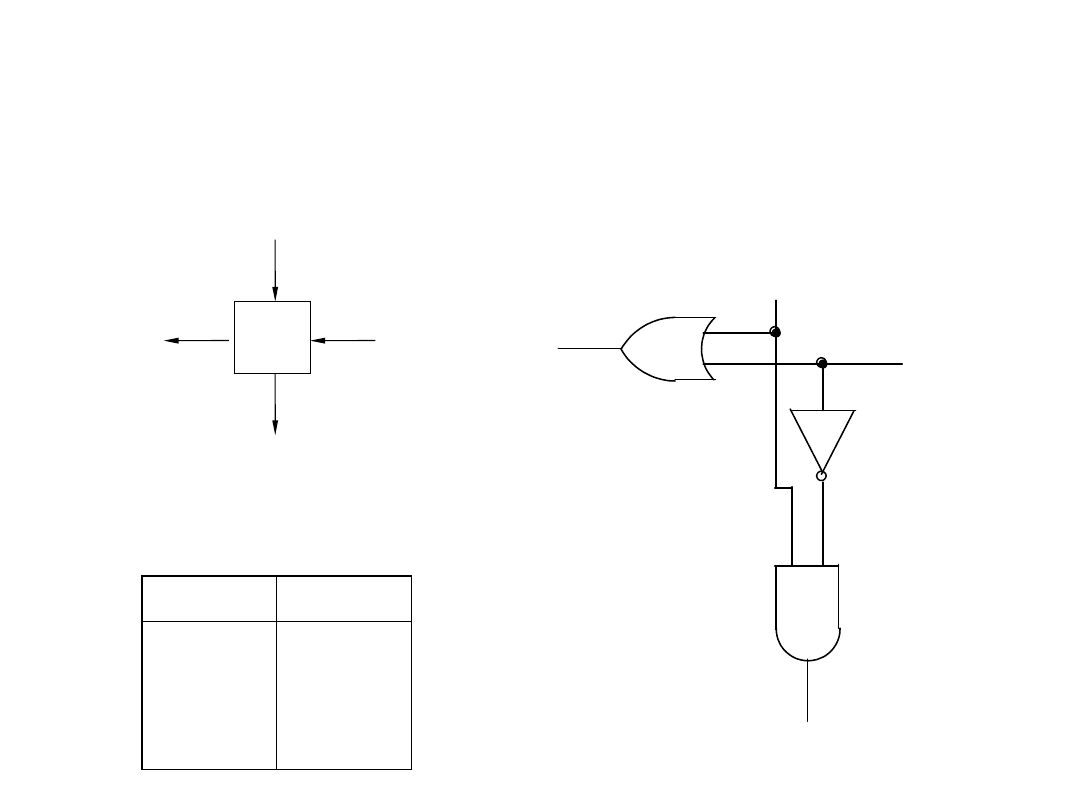
48

Zasada działania i-tego stopnia enkodera

priorytetowego

B

i+1

0

Y

i

B

i

E

i

Symbol

B

i+1

E

i

Y

i

B

i

0 0
0 1
1 0
1 1

0 0
1 1
0 1
0 1

Tabela prawdy

Schemat logiczny

i

Y

i

B

i+1

B

i

E

OR

NO

T

AN

D

0

1

1

1

1

1

1

1

1

0

1

0

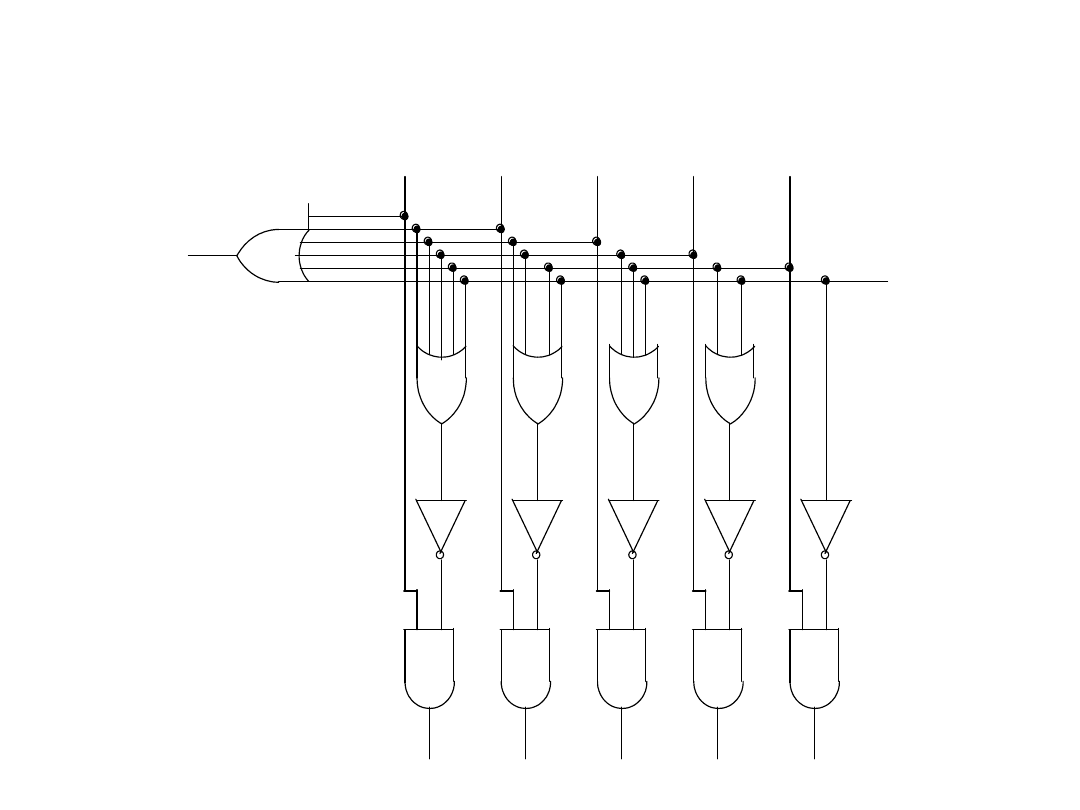
49

Układ enkodera priorytetowego

Realizacja z równoległą propagacją

przeniesienia

B

E

E

E

E

E

B

Y

Y

Y

Y

Y

5

0

1

2

3

4

4

3

2

1

0

0

B

4

3

B

2

B

B

1

1 z n

x z n

OR

OR

OR

OR

NO

T

NO

T

NO

T

NO

T

NA

ND

NA

ND

NA

ND

NA

ND

NO

T

NA

ND

OR

50

Wejścia

Wyjścia

x

0

x

1

A B C D

A B C D

0 0

1 0 0 0

0 1 1 1

0 1

0 1 0 0

1 0 1 1

1 0

0 0 1 0

1 1 0 1

1 1

0 0 0 1

1 1 1 0

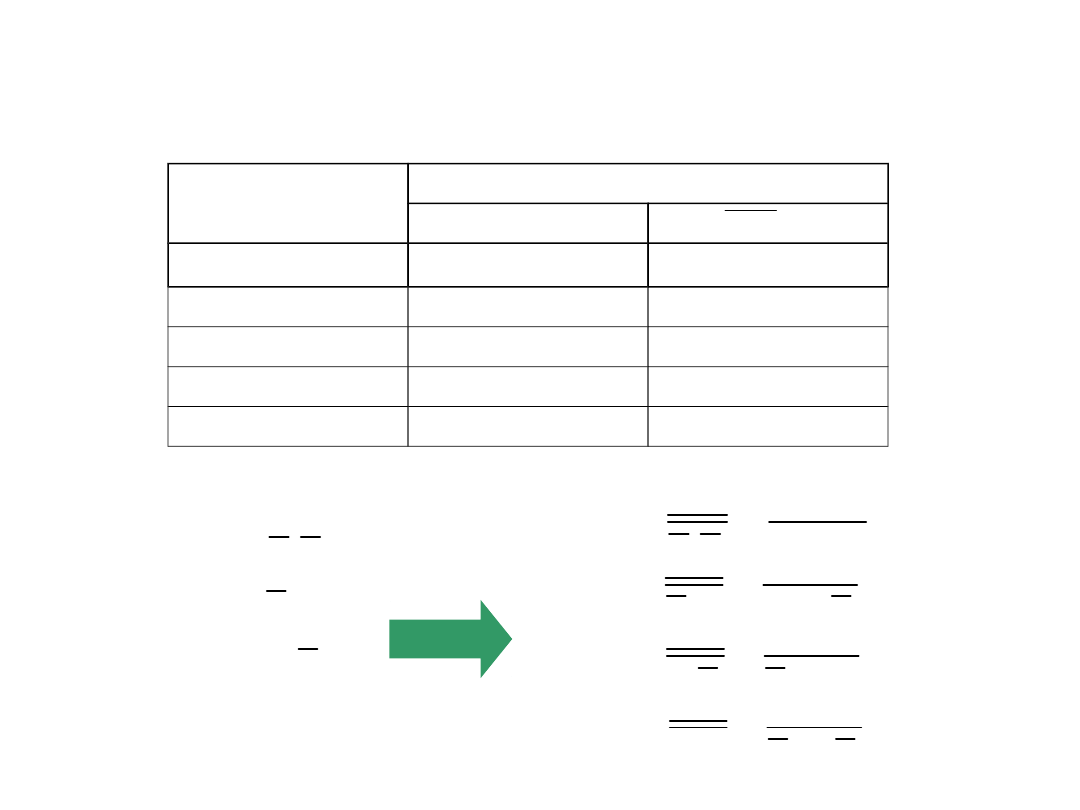
Układ dekodera pełnego

Tabela

prawdy

Równania dla dekodera kodu 8421

na 1 z 4

4

1z

4

1 z

0 1

0 1

0 1

B x x

C x x

D x x

=

=

=

0 1

A x x

=

0 1

0

1

A x x

x

x

=

= +

0 1

0

1

0 1

0

1

0 1

0

1

B x x

x

x

C x x

x

x

D x x

x

x

=

= +

=

= +

=

= +

POTOK X

51

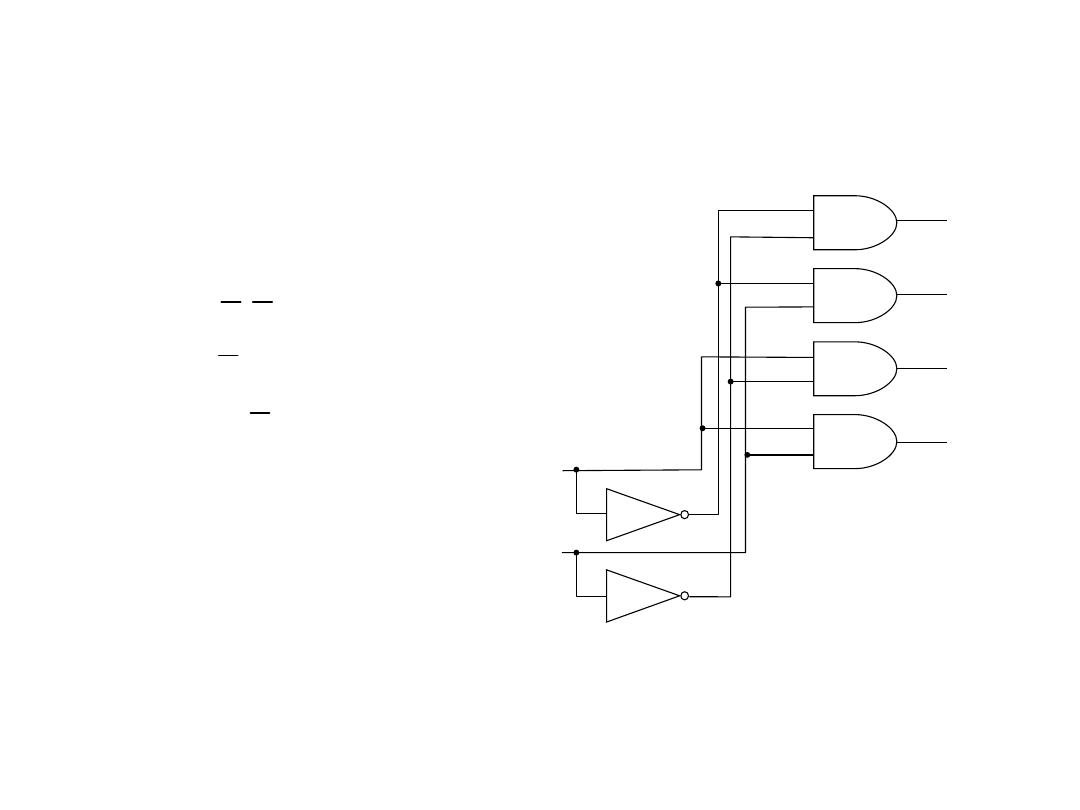
Układ dekodera pełnego

Realizacje układowe

NOT

NOT

x

0

x

1

A

B

C

D

AND

AND

AND

AND

1

z

4

0 1

0 1

0 1

B x x

C x x

D x x

=

=

=

0 1

A x x

=

Przykład:
dekoder8421_1z4.msm

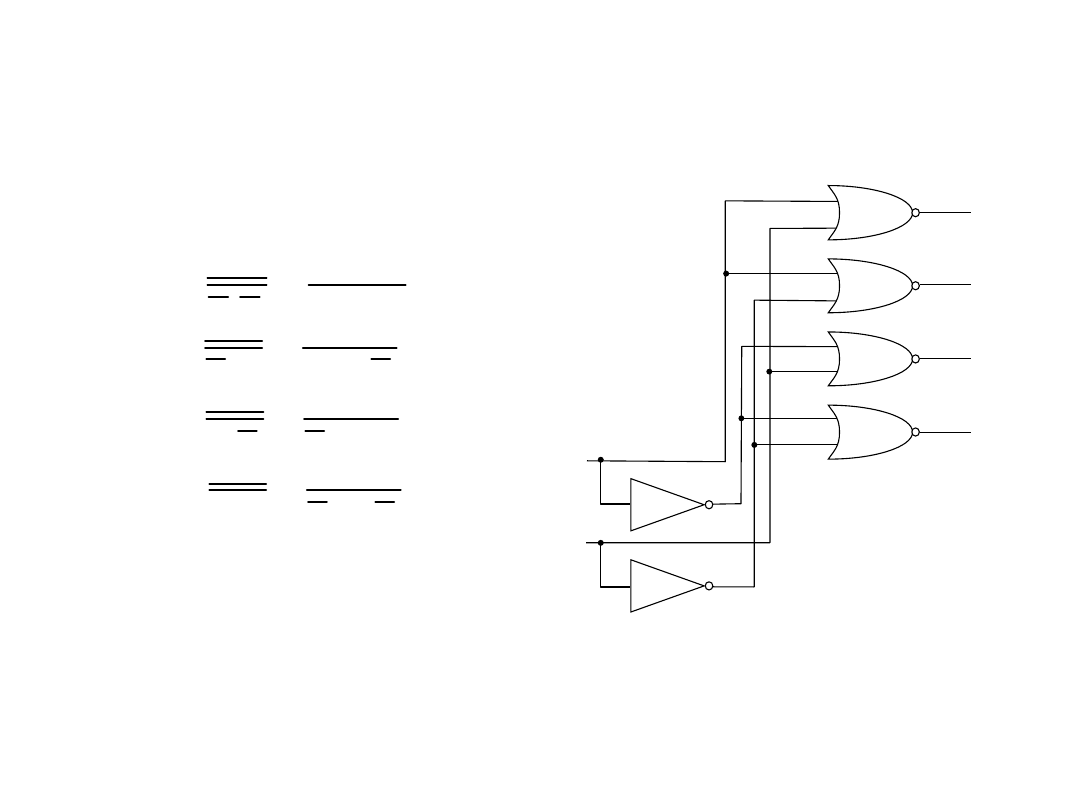
52

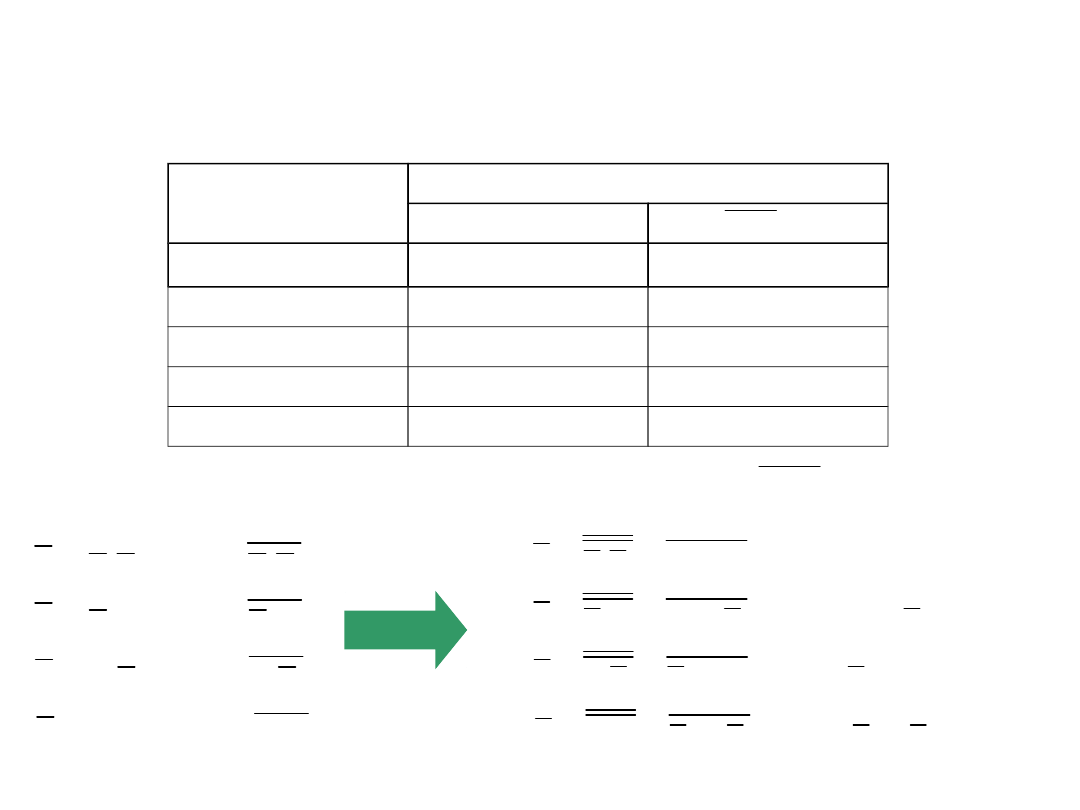
Układ dekodera pełnego

Realizacje układowe

NOT

NOT

A

B

C

D

NOR

NOR

NOR

NOR

1

z

4

x

0

x

1

0 1

0

1

A x x

x

x

=

= +

0 1

0

1

0 1

0

1

0 1

0

1

B x x

x

x

C x x

x

x

D x x

x

x

=

= +

=

= +

=

= +

53

Wejścia

Wyjścia

x

0

x

1

A B C D

A B C D

0 0

1 0 0 0

0 1 1 1

0 1

0 1 0 0

1 0 1 1

1 0

0 0 1 0

1 1 0 1

1 1

0 0 0 1

1 1 1 0

Układ dekodera pełnego

Tabela

prawdy

4

1z

4

1 z

Równania dla dekodera kodu 8421
na

4

1 z

0 1

0 1

0 1

0 1

0 1

0 1

0 1

0 1

A x x

A x x

B x x

B x x

C x x

C x x

D x x

D x x

























0 1

0

1

0

1

0 1

0

1

0

1

0 1

0

1

0

1

0 1

0

1

0

1

A x x

x

x

A x

x

B x x

x

x

B x

x

C x x

x

x

C x

x

D x x

x

x

D x

x



  

 



  

 



  

 



  

 

54

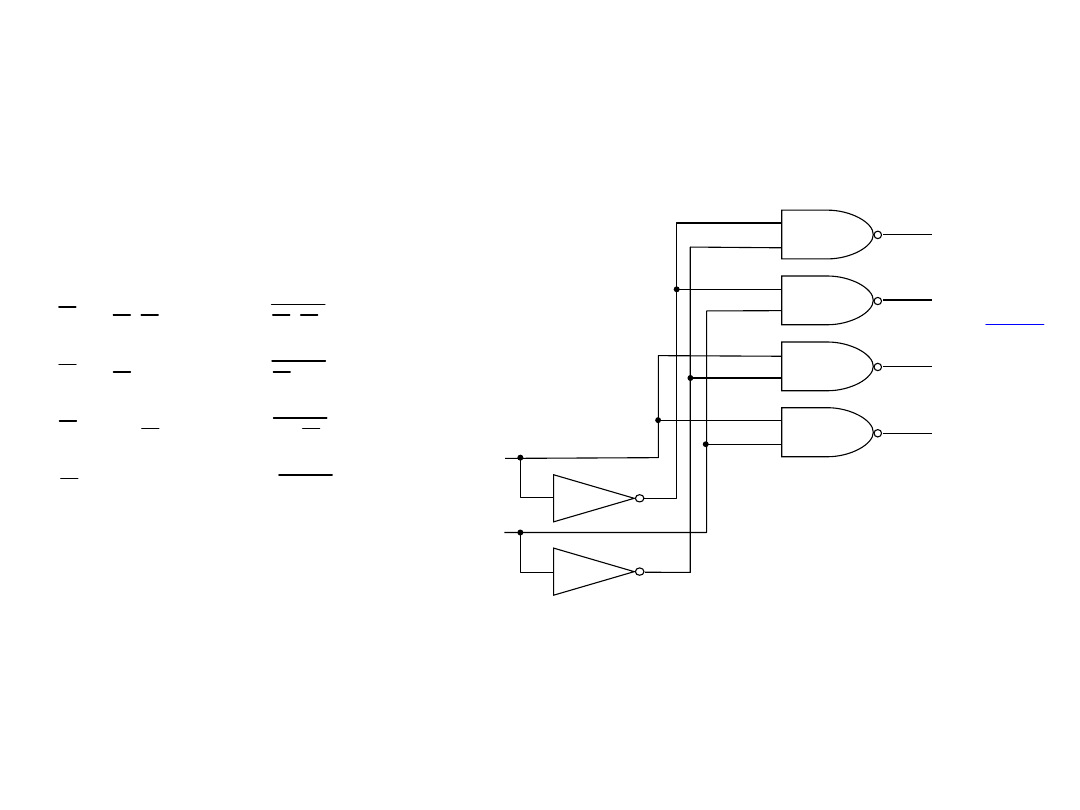
Układ dekodera pełnego

Realizacje układowe

Przykład:
dekoder8421_nie_1z4.msm

NOT

NOT

x

0

x

1

A

B

C

D

NAN

D

NAN

D

NAN

D

NAN

D

1 4

z

0 1

0 1

0 1

0 1

0 1

0 1

0 1

0 1

A x x

A x x

B x x

B x x

C x x

C x x

D x x

D x x

























55

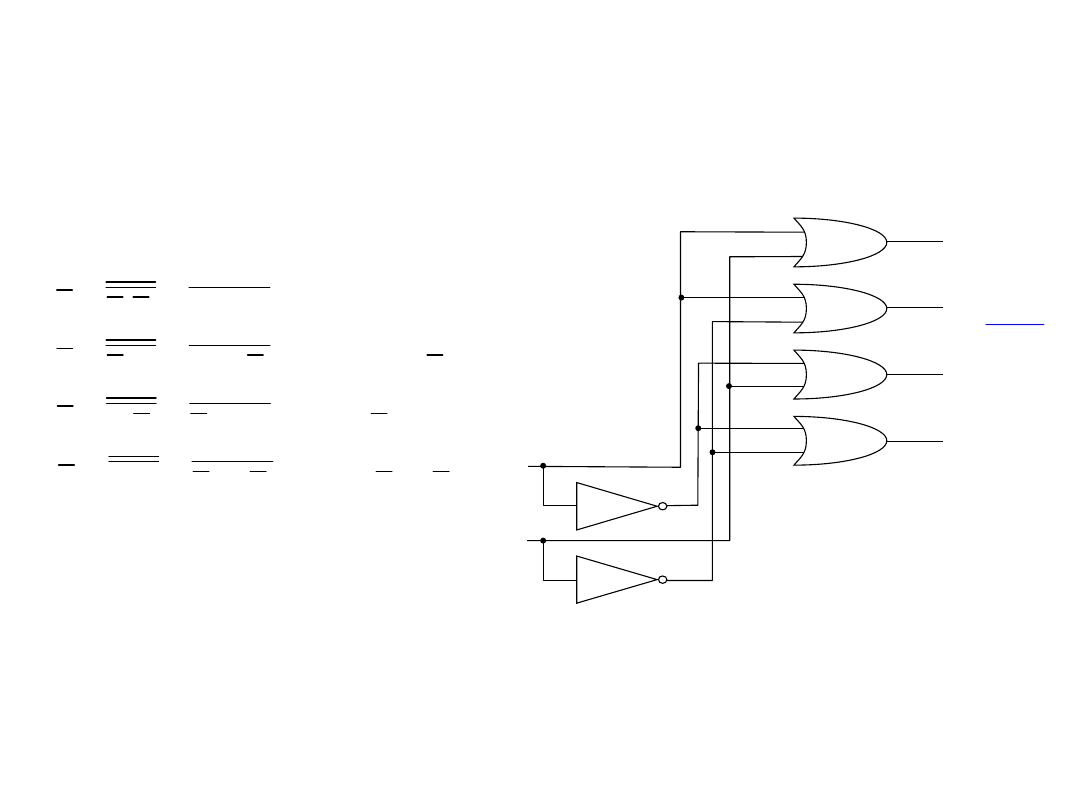
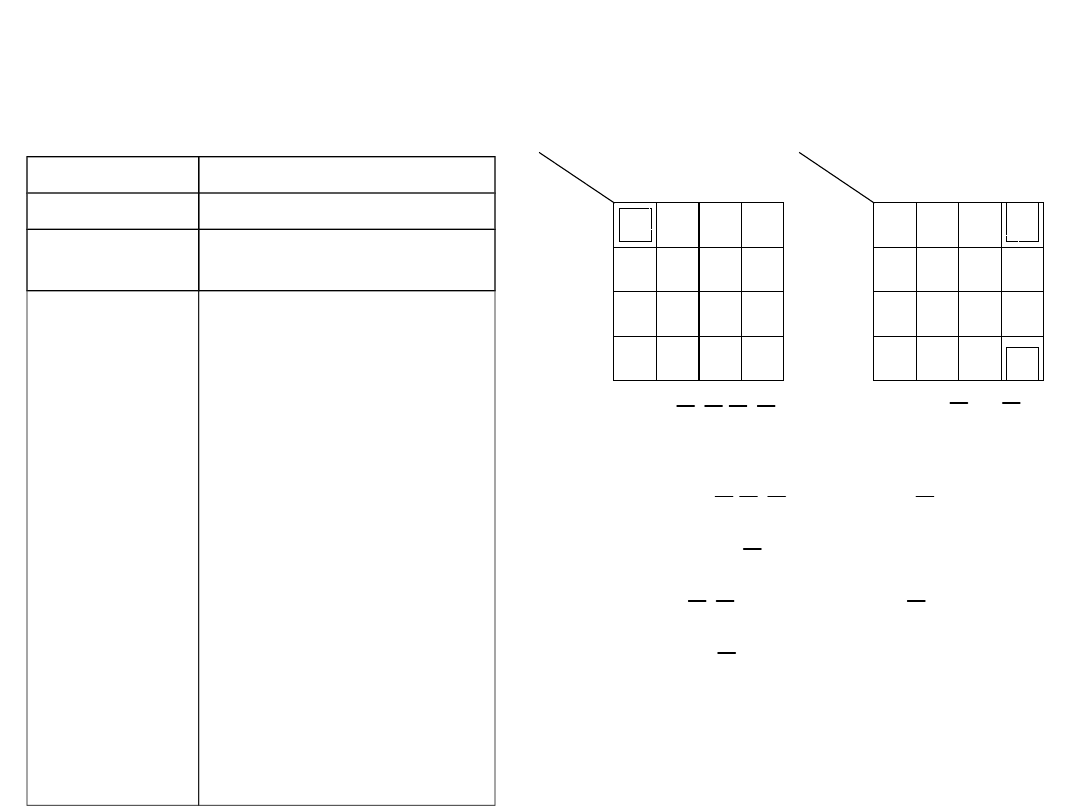
Układ dekodera pełnego

Realizacje układowe

NOT

NOT

A

B

C

D

OR

OR

OR

OR

x

0

x

1

1 4

z

0 1

0

1

0

1

0 1

0

1

0

1

0 1

0

1

0

1

0 1

0

1

0

1

A x x

x

x

A x

x

B x x

x

x

B x

x

C x x

x

x

C x

x

D x x

x

x

D x

x



  

 



  

 



  

 



  

 

56

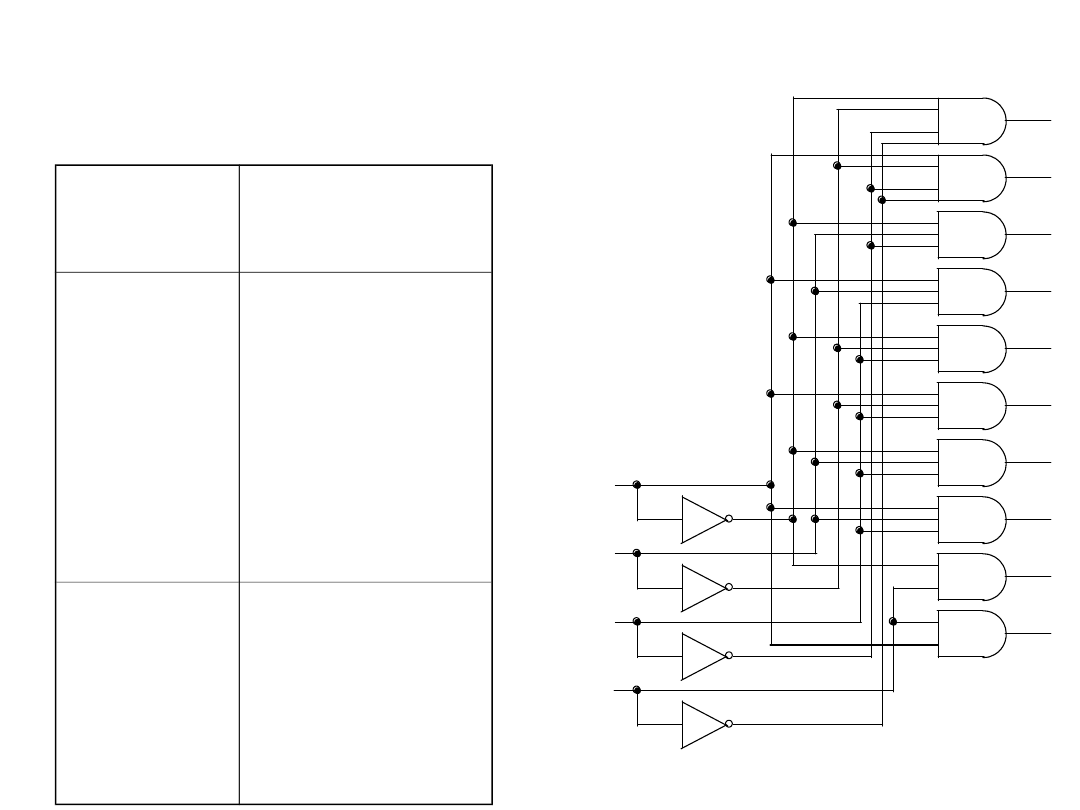
Układ dekodera niepełnego

Tabela

prawdy

Wejścia

Wyjścia

BCD 8421

1 z 10

X

3

X

2

X

1

X

0

A B C D E F G H

I J

0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1

1 0 0 0 0 0 0 0

0 0

0 1 0 0 0 0 0 0

0 0

0 0 1 0 0 0 0 0

0 0

0 0 0 1 0 0 0 0

0 0

0 0 0 0 1 0 0 0

0 0

0 0 0 0 0 1 0 0

0 0

0 0 0 0 0 0 1 0

0 0

0 0 0 0 0 0 0 1

0 0

0 0 0 0 0 0 0 0

1 0

0 0 0 0 0 0 0 0

0 1

1

0

0

0

0

0

0

0

--- --- --- ---

0

0 --- ---

10

11

01

00

00 01 11 10

x

1

x

0

x

3

x

2

A

0

0

0

1

0

0

0

0

--- --- --- ---

0

0 --- ---

10

11

01

00

00 01 11 10

C

x

3

x

2

x

1

x

0

0 1 2 3

A x x x x

=

0 1 2

C x x x

=

0 1 2

0 1 2

0 3

0 3

G x x x

H x x x
I x x

J

x x

=

=

=

=

0 1 2 3

0 1 2

0 1 2

0 1 2

B x x x x
D x x x
E x x x
F x x x

=

=

=

=

57

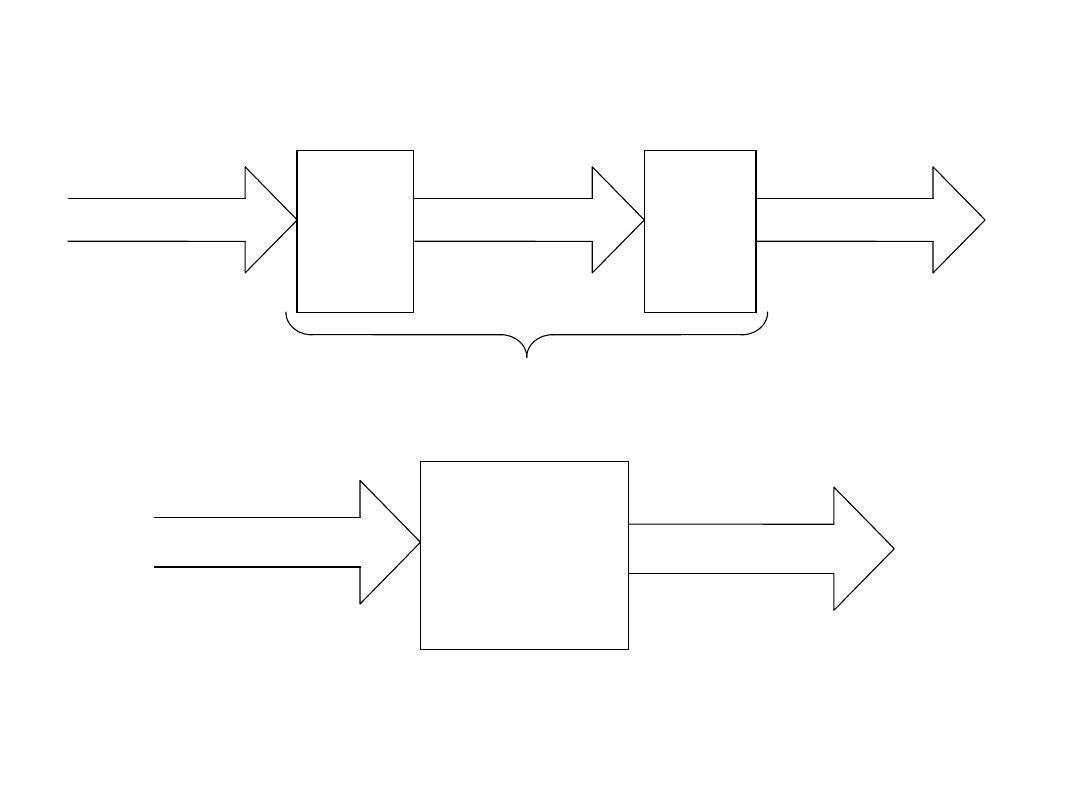
Układ dekodera niepełnego

A

B

C

D

E

F

G

H

I

J

X

3

2

X

1

X

X

0

AND

AND

AND

AND

AND

AND

AND

AND

AND

AND

NOT

NOT

NOT

NOT

Kod

wejściowy

x

3

x

2

x

1

x

0

Nr aktywnego

wyjścia

0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1

A
B
C

D

E

F

G
H

I
J

Stany zabronione

1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1

C, I

D, J

E, I

F, J

G, I
H, J

Tabela stanów dekodera

Przykład:
dekoder_8421_1z10.msm

58

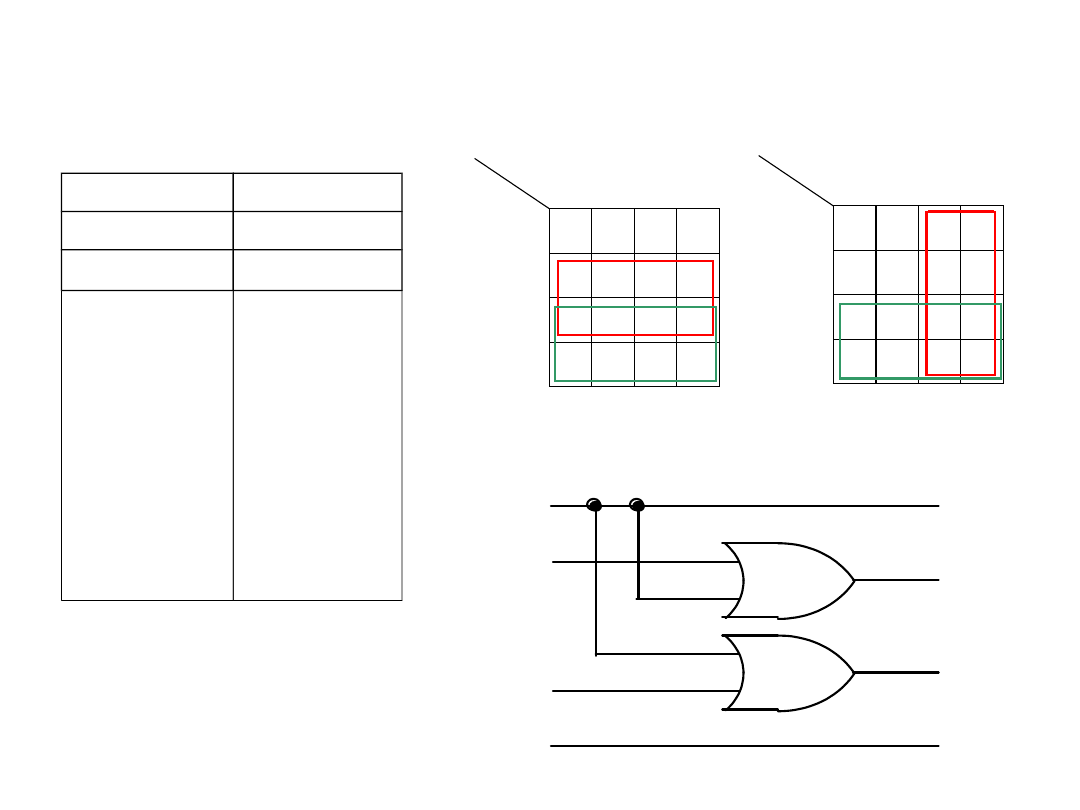
Układ transkodera

Kod wejściowy

X

Kod pierścieniowy

Kod wejściowy

Y

DEKODER

ENKODER

Transkoder

TRANSKODER

Kod wejściowy Y

Kod wejściowy X

POTOK Y

59

Układ transkodera

Tabela

prawdy

Wejścia

Wyjścia

8 4 2 1

2 4 2 1

X

3

X

2

X

1

X

0

A B C D

0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1

0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 1 1 0

1 1 1 1

2

3

= +

B

x

x

3

1

C

x

x

= +

A = x

3

D = x

0

0

0

0

0

1

1

1

1

--- --- --- ---

1

1 --- ---

10

11

01

00

00 01 11 10

x

1

x

0

x

3

x

2

B

0

0

1

1

0

0

1

1

--- --- --- ---

1

1 --- ---

10

11

01

00

00 01 11 10

C

x

3

x

2

x

1

x

0

X

3

X

2

1

X

0

X

A

B

C

D

OR

OR

60

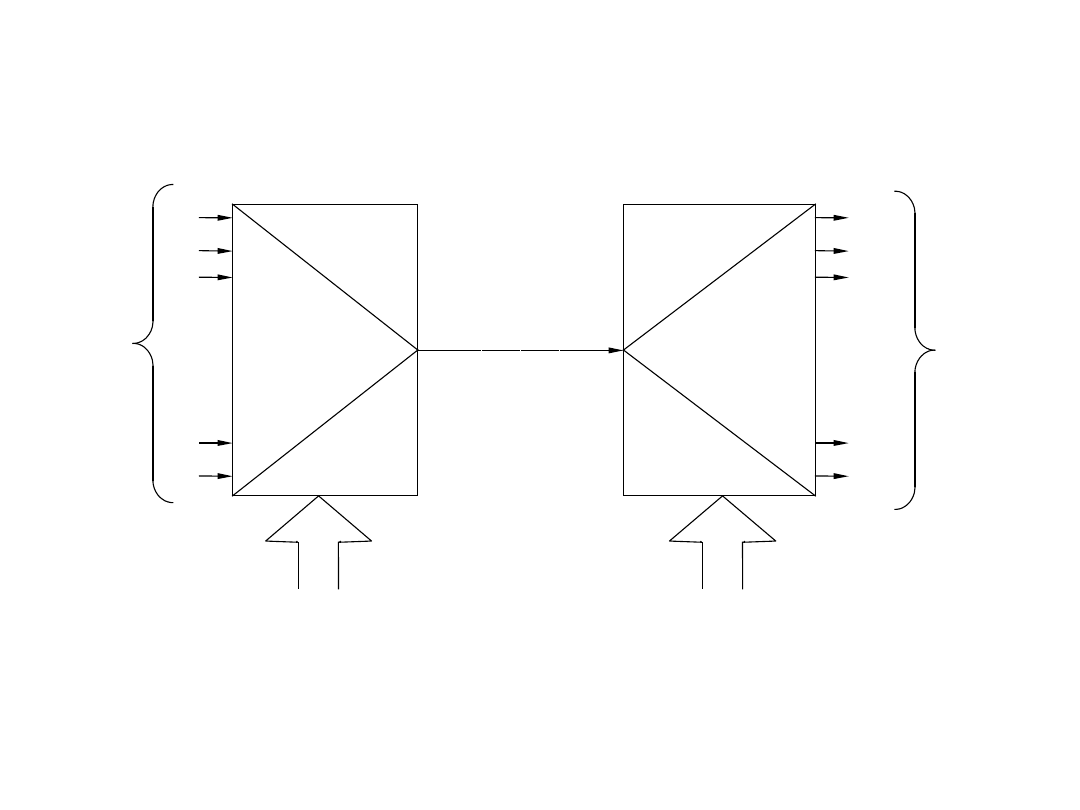
Multipleksery i demultipleksery

Multiplekser

Demultiplekser

Linia

przesyłowa

W

E

J

Ś
C

I

A

W

Y

J

Ś
C

I

A

0
1
2

n-1

n

0
1
2

n-1

n

Adres

Adres

61

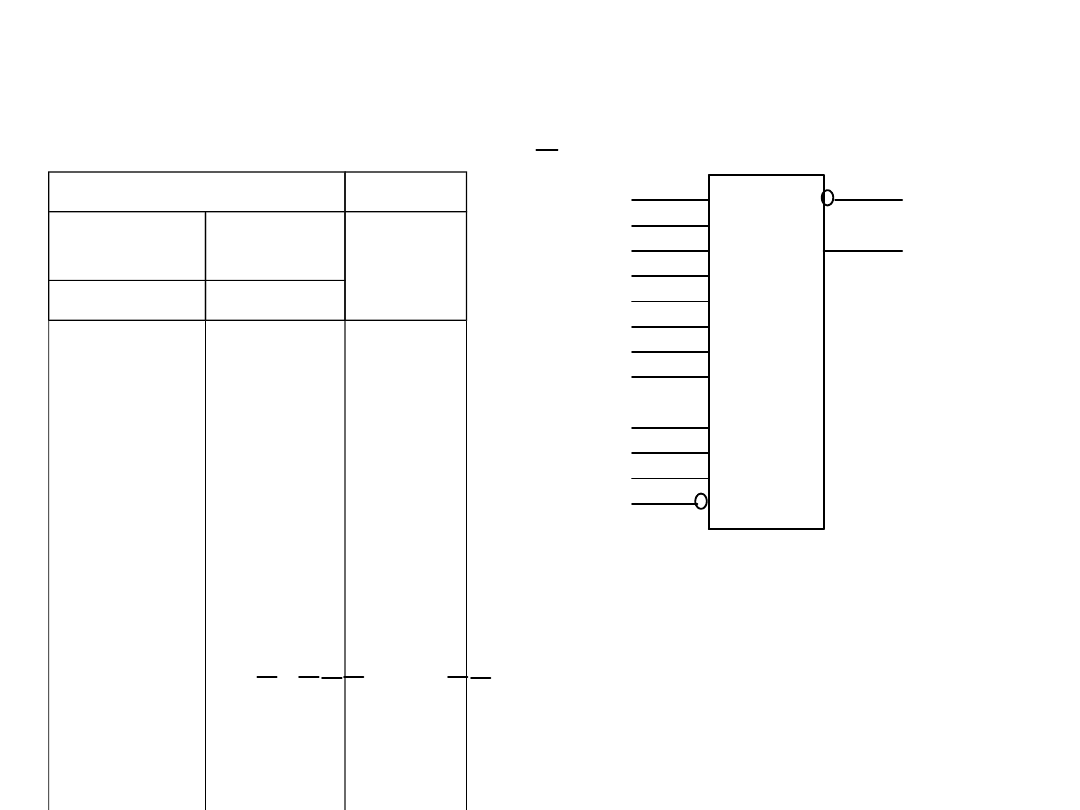
Multiplekser scalony 74151

Wejścia

Wyjścia

Adresowe

Strobując

e

Y W

C B A

S

X X X

0 0 0

0 0 1

0 1 0

0 1 1

1 0 0

1 0 1

1 1 0

1 1 1

1

0

0

0

0

0

0

0

0

0 1

D

0

D

0

’

D

1

D

1

’

D

2

D

2

’

D

3

D

3

’

D

4

D

4

’

D

5

D

5

’

D

6

D

6

’

D

7

D

7

’

Tabela

stanów

Wyjścia

komplementarne

Wejścia

informacyjne

Wejścia

adresowe

Wejście strobujace

74151

D0
D1
D2
D3
D4
D5
D6
D7

A
B
C
S

W

Y

Symbol

Funkcja realizowana przez

układ:

0

1

7

(

)

Y S CBAD CBAD

CBAD

=

+

+ +

K

62

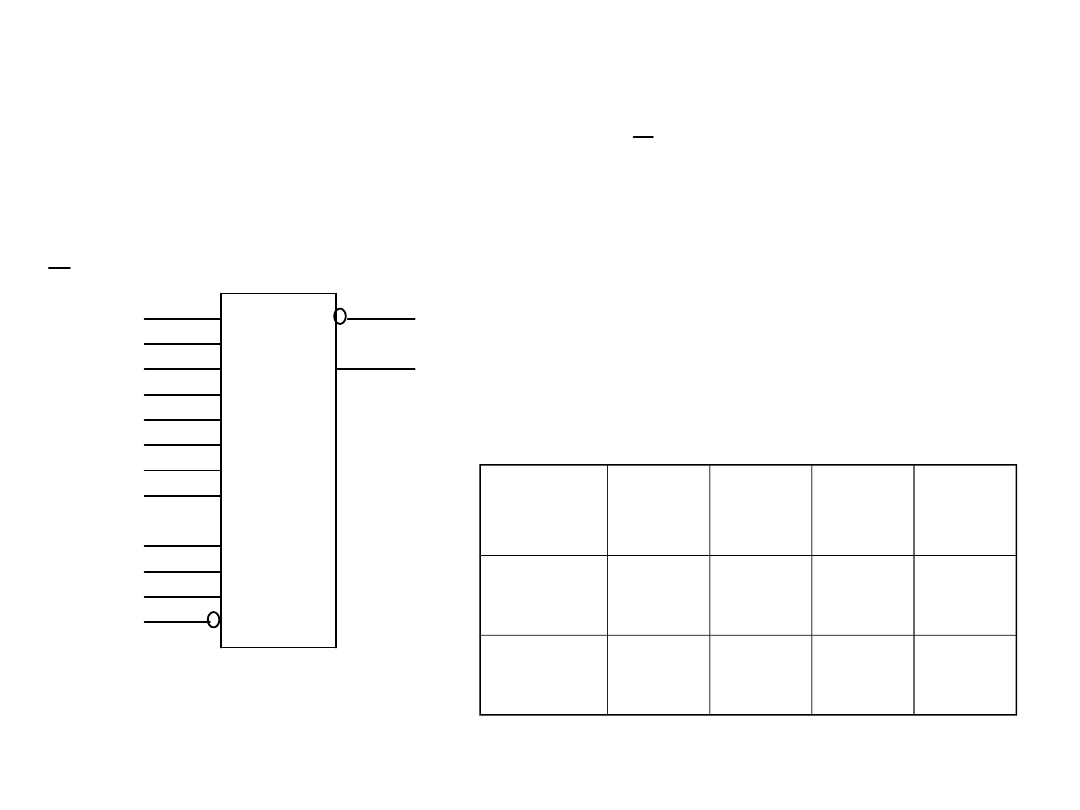
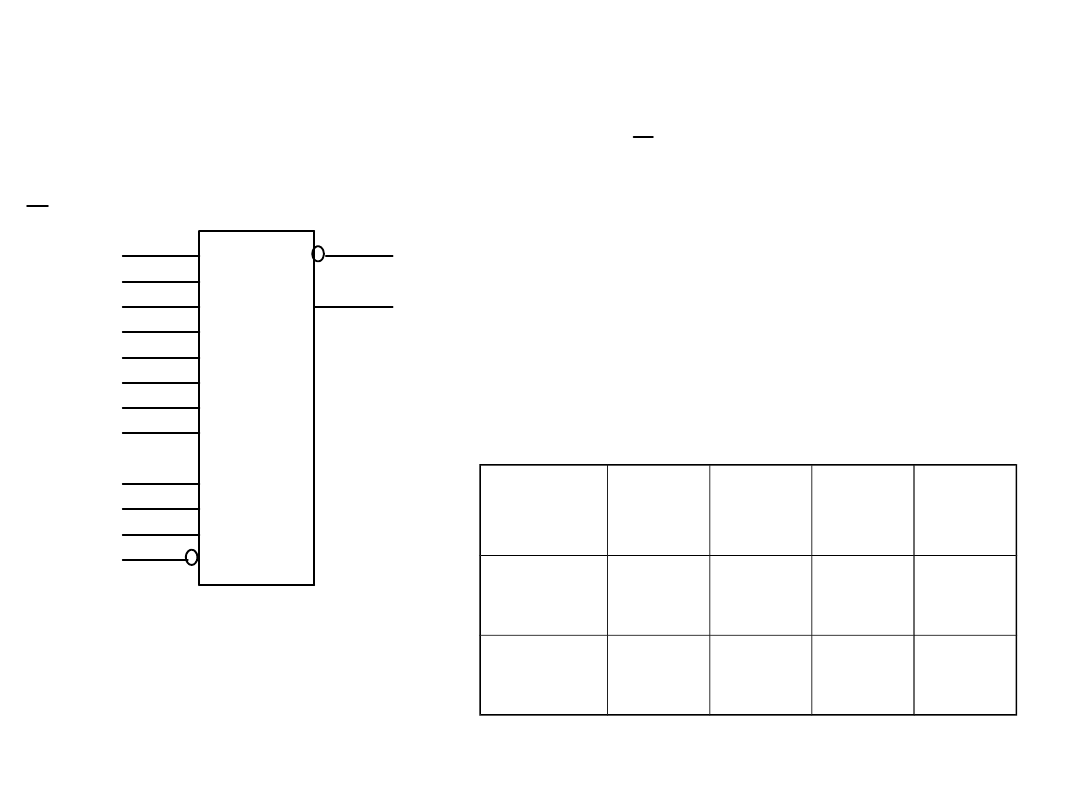
Realizacja funkcji przełączającej za pomocą

multipleksera

*

*

* *

F a b b c a b c

=

+

+

Wyjścia

komplementarne

Wejścia

informacyjne

Wejścia

adresowe

Wejście strobujace

74151

D0
D1
D2
D3
D4
D5
D6
D7

A
B
C
S

W

Y

ba

c

00

01

11

10

0

1

0

1

3

2

4

5

7

6

?

?

?

?

?

?

?

?

63

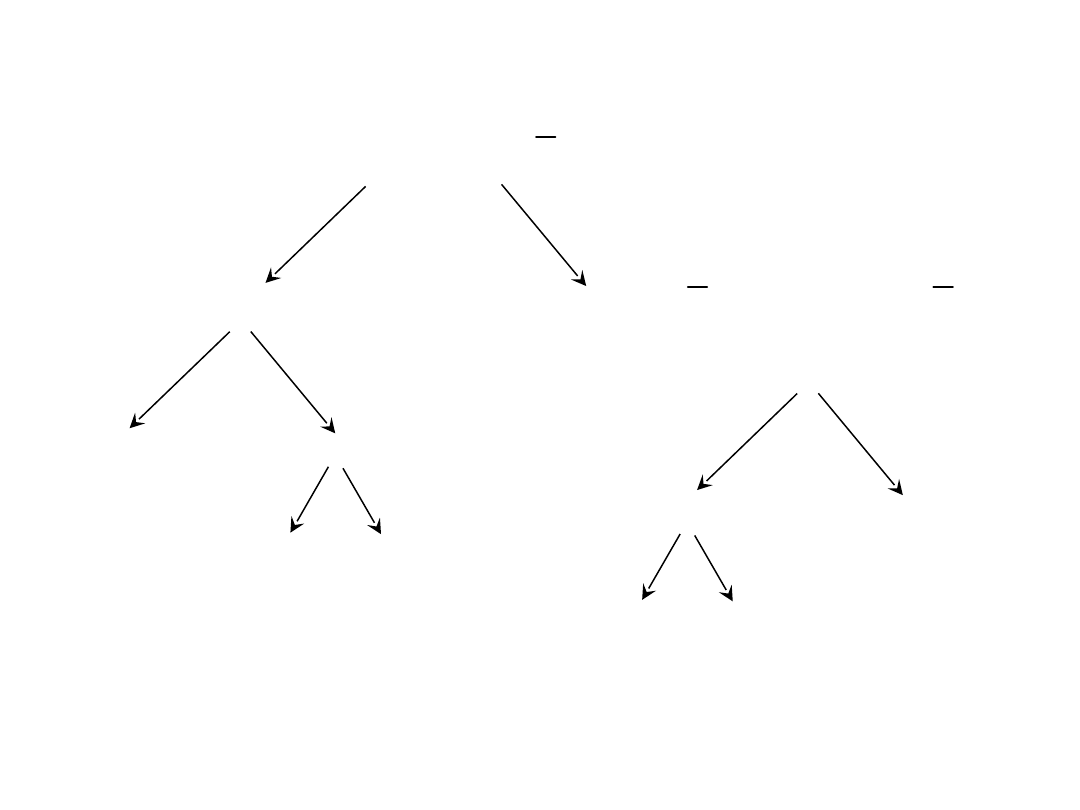
Realizacja funkcji przełączającej za pomocą

multipleksera

*

*

* *

F a b b c a b c

=

+

+

*

b c

*

*

(

)

b b c b c

b

b c

b

c

b

+

+

= +

=

=

+

+

0

a =

1

a =

0

b=

1

b=

0

b=

1

b=

0

c

1

c

0

c =

1

c =

0

c =

1

c =

1

0

1

0

1

{(110);(101);(011);(111)}

F =

0

{(000);(100);(010);(001)}

F =

64

Realizacja funkcji przełączającej za pomocą

multipleksera

*

*

* *

F a b b c a b c

=

+

+

Wyjścia

komplementarne

Wejścia

informacyjne

Wejścia

adresowe

Wejście strobujace

74151

D0
D1
D2
D3
D4
D5
D6
D7

A
B
C
S

W

Y

ba

c

00

01

11

10

0

1

0

1

3

2

4

5

7

6

0

0

1

0

0

1

1

1

1

{(110);(101);(011);(111)}

F =

0

{(000);(100);(010);(001)}

F =

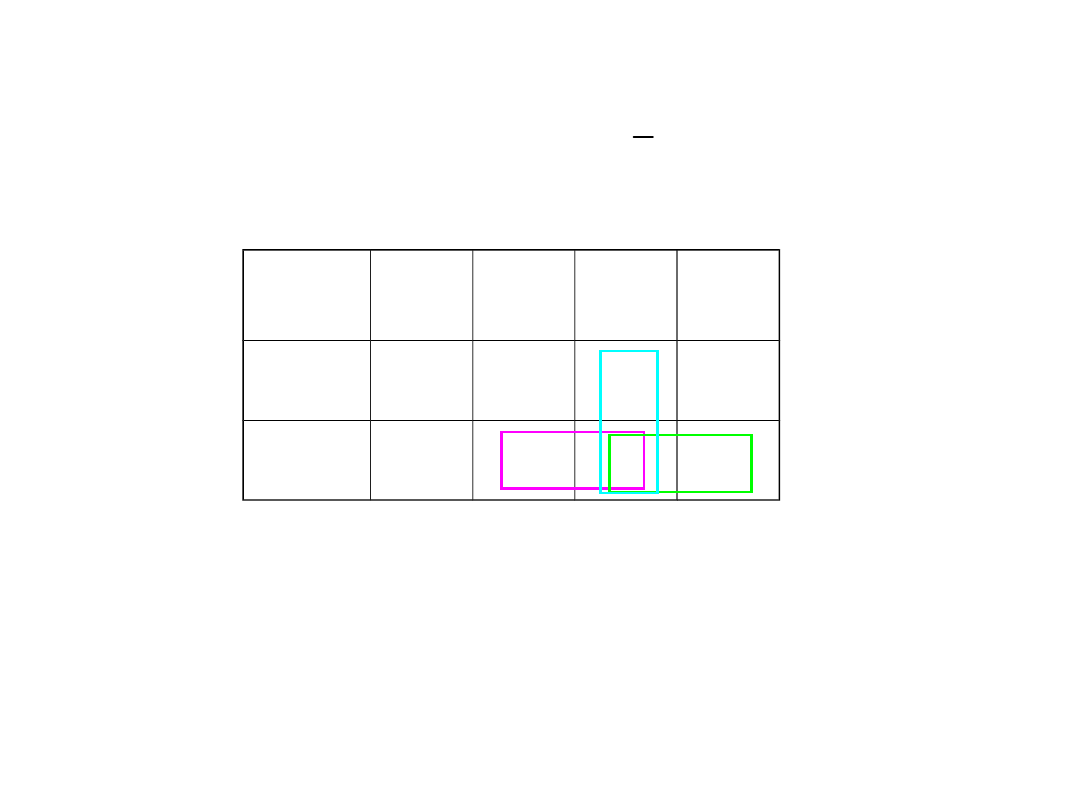
65

Realizacja funkcji przełączającej za pomocą

multipleksera

*

*

* *

F a b b c a b c

=

+

+

ba

c

00

01

11

10

0

1

0

1

3

2

4

5

7

6

0

0

1

0

0

1

1

1

*

)

*

*

*(

*

c b

F

a b

b a

a

c c b

c

=

+

+

=

+ +

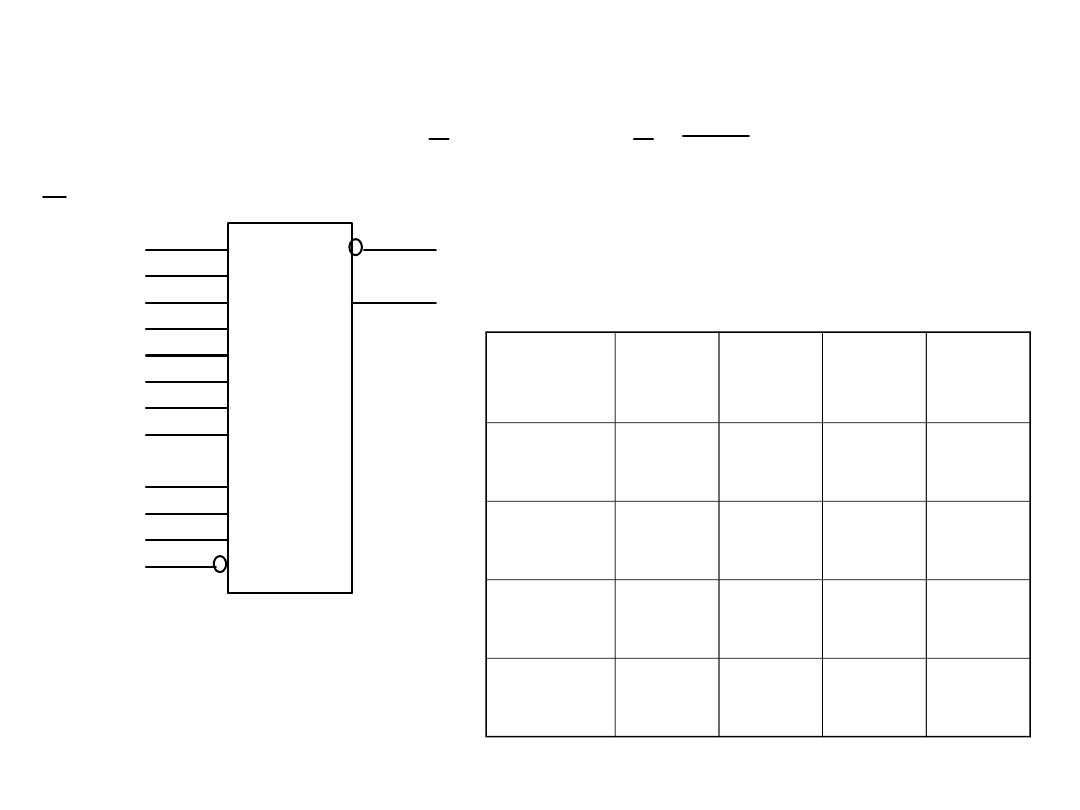
66

ba

dc

00

01

11

10

00

01

11

10

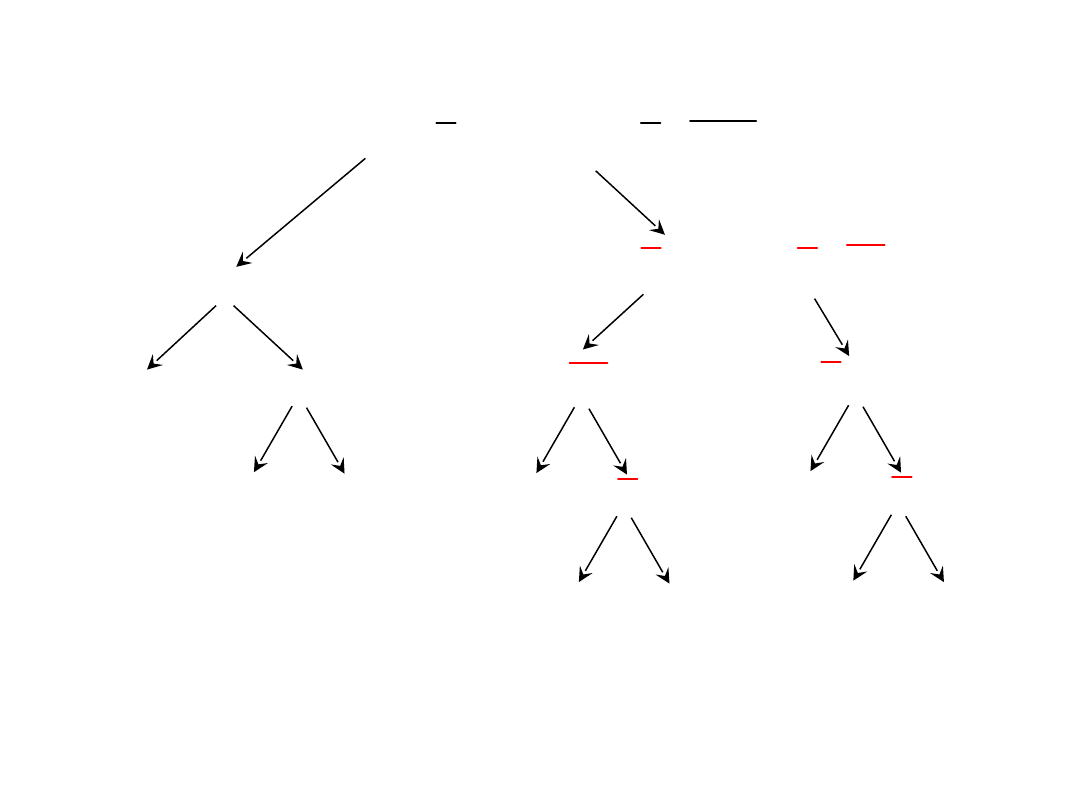
Realizacja funkcji przełączającej za pomocą

multipleksera

* *

*

* * *

F a b d b c a b c d

=

+

+

Wyjścia

komplementarne

Wejścia

informacyjne

Wejścia

adresowe

Wejście strobujace

74151

D0
D1
D2
D3
D4
D5
D6
D7

A
B
C
S

W

Y

0

1

3

2

4

5

7

6

0

1

3

2

4

5

7

6

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

67

Realizacja funkcji przełączającej za pomocą

multipleksera

* *

*

* * *

F a b d b c a b c d

=

+

+

*

b c

*

*

*

b d b c b cd

+

+

0

c

0

c =

1

c =

0

c =

1

c =

d

1

1

0

1

{(0110);(1110);(0001);(1001);(0101);(1111);(0011);(0111);}

F =

0

{(0000);(0100);(1000);(1100);(0010);(1010);(1101);(1011);}

F =

0

a =

1

a =

0

b=

1

b 

0

b=

1

b=

cd

d c

+

1

c =

0

c =

d

1

0

d =

1

d =

0

1

0

d =

1

d =

0

1

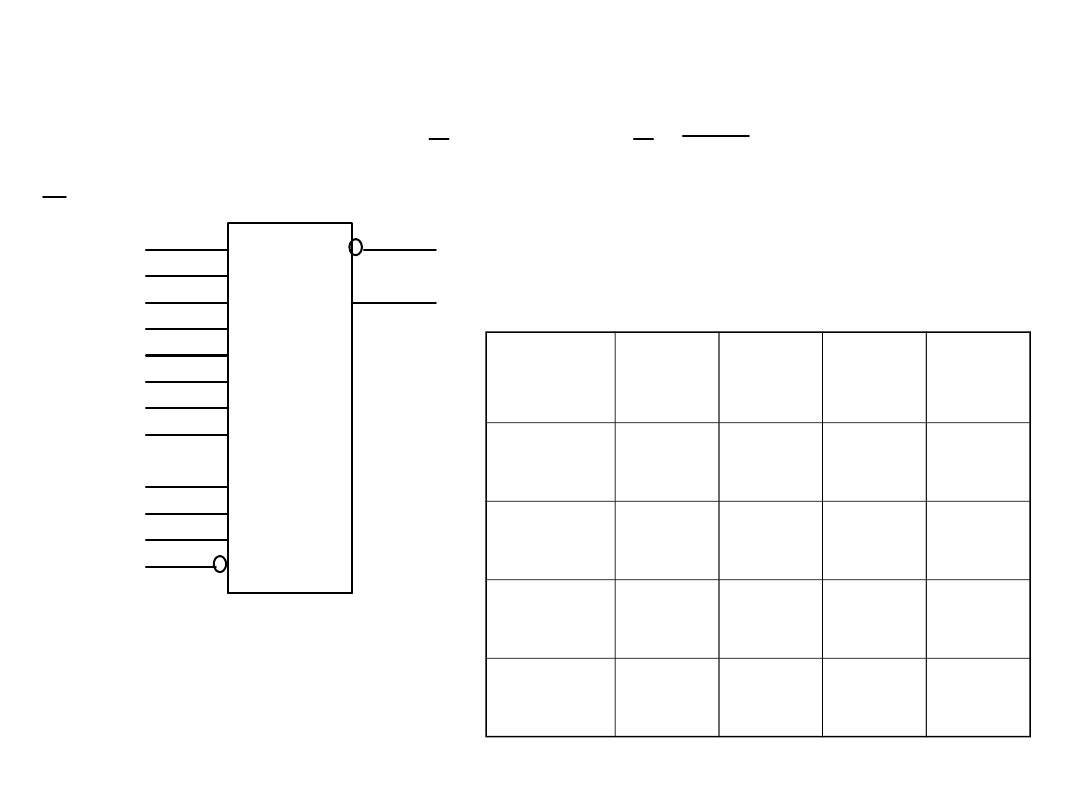
68

ba

dc

00

01

11

10

00

01

11

10

Realizacja funkcji przełączającej za pomocą

multipleksera

* *

*

* * *

F a b d b c a b c d

=

+

+

Wyjścia

komplementarne

Wejścia

informacyjne

Wejścia

adresowe

Wejście strobujace

74151

D0
D1
D2
D3
D4
D5
D6
D7

A
B
C
S

W

Y

0

1

3

2

4

5

7

6

0

1

3

2

4

5

7

6

0

1

1

0

0

1

1

1

0

1

0

0

0

0

1

1

69

ba

dc

00

01

11

10

00

01

11

10

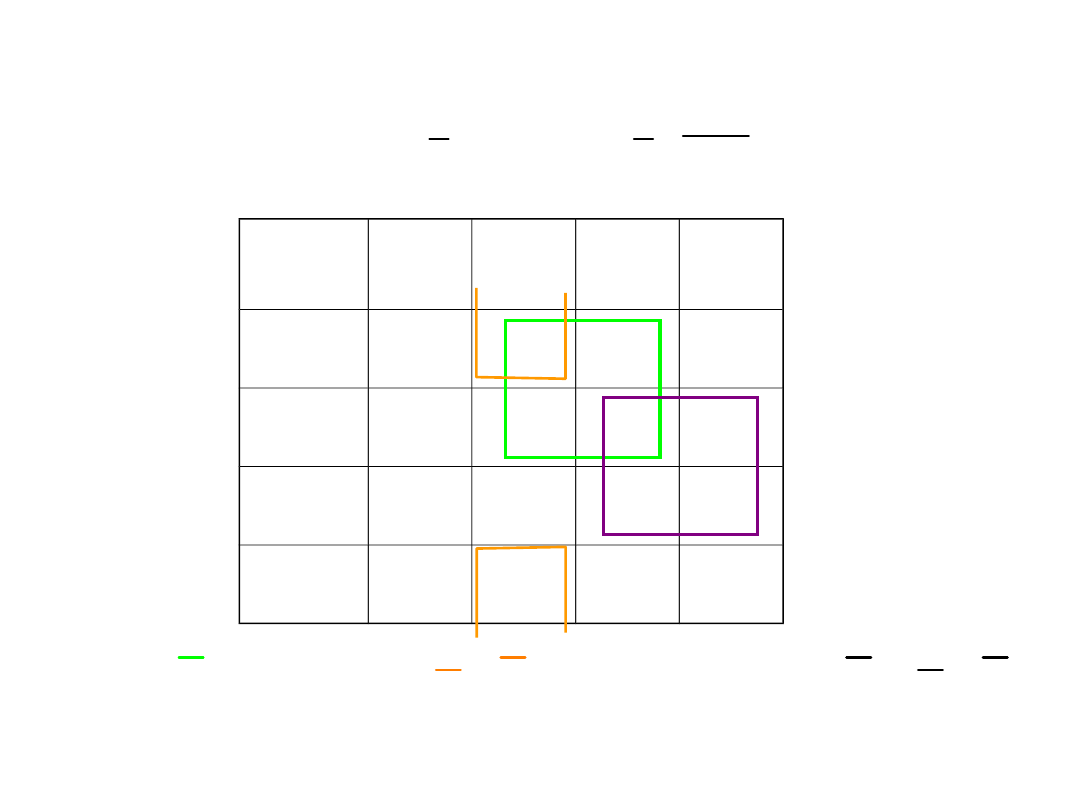
Realizacja funkcji przełączającej za pomocą

multipleksera

* *

*

* * *

F a b d b c a b c d

=

+

+

0

1

3

2

4

5

7

6

0

1

3

2

4

5

7

6

0

1

1

0

0

1

1

1

0

1

0

0

0

0

1

1

*

*(

* )

*

*

*

*

c b a

F

c b a

d a

d

c b

c b

=

+

+

=

+

+

70

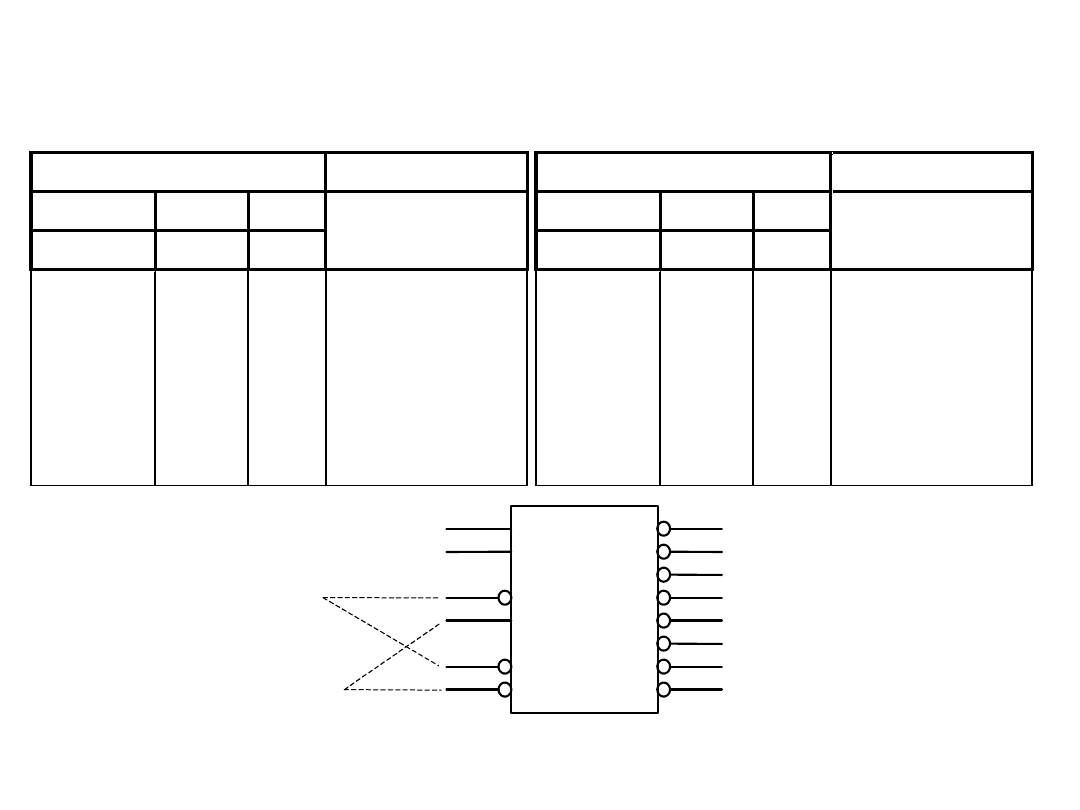
Demultiplekser scalony 74155

a )

W e jś c ia

W y jś c ia

A d re s o w e

S tro b .

In fo r.

B A

G

2

C

2

2 Y

0

2 Y

1

2 Y

2

2 Y

3

X X
0 0
0 1
1 0
1 1
X X

1
0
0
0
0

X

X

0
0
0
0
1

1 1 1 1
0 1 1 1
1 0 1 1
1 1 0 1
1 1 1 0
1 1 1 1

W e jś c ia

W y jś c ia

A d re s o w e

S tro b .

In fo r.

B A

G

1

C

1

1 Y

0

1 Y

1

1 Y

2

1 Y

3

X X
0 0
0 1
1 0
1 1
X X

1
0
0
0
0

X

X

1
1
1
1
0

1 1 1 1
0 1 1 1
1 0 1 1
1 1 0 1
1 1 1 0
1 1 1 1

b )

W ejścia adresowe

W ejścia

strobujące

W ejścia

informacyjne

W yjścia

informacyjne

W yjścia

informacyjne

7 4 1 5 5

A
B

1 G
1 C

2 G
2 C

1 Y 0
1 Y 1
1 Y 2
1 Y 3
2 Y 0
2 Y 1
2 Y 2
2 Y 3

71

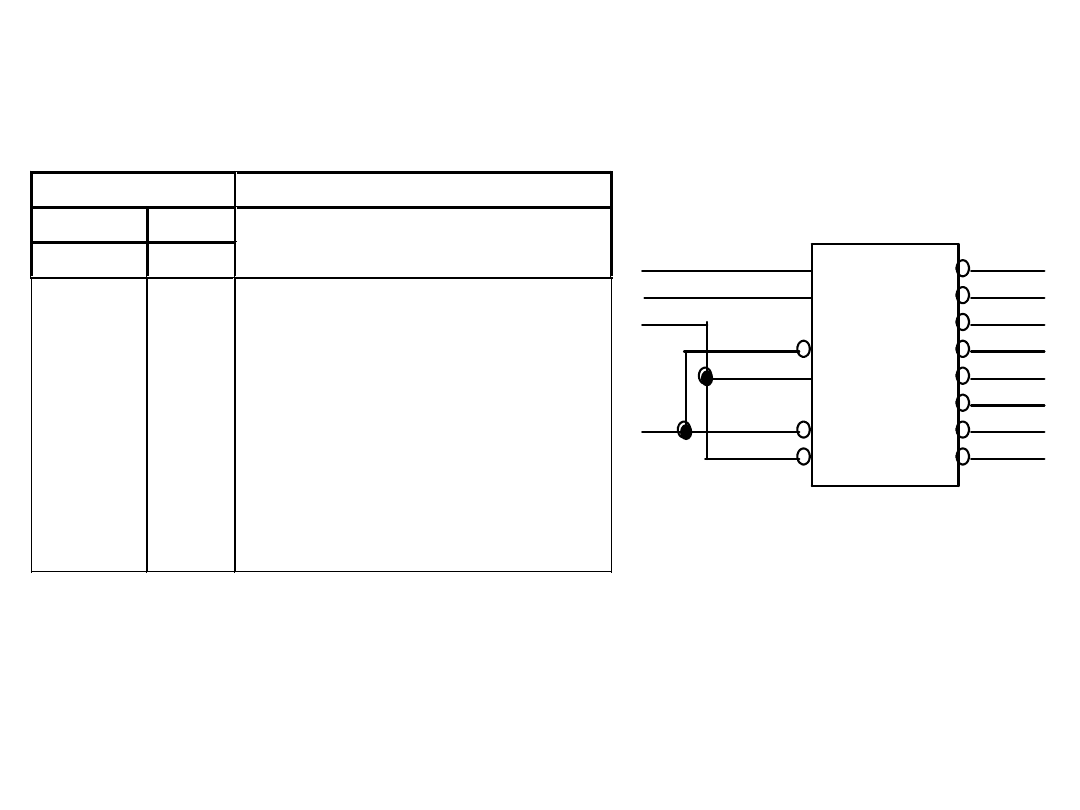
Realizacja demultipleksera 8-bitowego

Wejścia

Wyjścia

Adresowe Strob.

C B A

G

2Y

0

2Y

1

2Y

2

2Y

3

1Y

0

1Y

1

1Y

2

1Y

3

X X X
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

1
0
0
0
0
0
0
0
0

1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1
1 0 1 1 1 1 1 1
1 1 0 1 1 1 1 1
1 1 1 0 1 1 1 1
1 1 1 1 0 1 1 1
1 1 1 1 1 0 1 1
1 1 1 1 1 1 0 1
1 1 1 1 1 1 1 0

A

B

C

G

74155

A
B

1G
1C

2G
2C

1Y0
1Y1
1Y2
1Y3
2Y0
2Y1
2Y2
2Y3