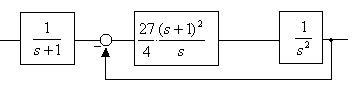Wykład 5

DYNAMIKA I STABILNOŚĆ

5.1.

Odpowiedź układu drugiego rzędu

5.2.

Ekstrema odpowiedzi oscylacyjnej

5.3.

Wpływ dodatkowego zera i bieguna

5.4.

Upraszczanie transmitancji wyższych rzędów 5.5.

Eliminacja przeregulowania przez filtrację wielkości zadanej 5.6.

Stabilność układów ze sprzężeniem zwrotnym

5.1.

Odpowiedź układu drugiego rzędu

• Serwomechanizm ze sterowaniem prą dowym (Wykład 1) w

k

y

2

s

k

k

P

=

α = T

J

d

1 + s

α

sprzężenie tachometryczne i pozycyjne

Transmitancja:

k

Y ( s

2

) =

s

=

k

=

W ( s)

1

( + s

α ) k

s 2 + α ks +

1 +

k

s 2

2

ω n

= 2

2

s + 2ξω s + ω

n

n

gdzie: ω - częstotliwość drgań naturalnych (niegasnących) n

ξ - współczynnik tłumienia

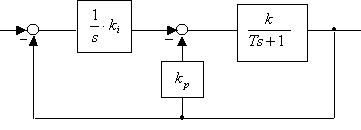
• Układ regulacji poziomu (Wykład 3)

„Rozdzielony” reulator PI

I

O

w

1 k

k

p

y

s T

Ts +1

i

k

P

p

w

y

I

O

P

1

1 k

1

k

PI:

k 1

( +

) = k

p

+

= k + k ,

gdzie

p

k =

p

T s

p

s T

p

i s

i

T

i

i

i

O

k

k

I

i

Y ( s)

1 +

IO

OP

s Ts +

=

=

=

1

=

W ( s)

O

1 + PO + IO

k

k

k

1 + I

1 + k p

+ i

1 + OP

Ts + 1

s Ts + 1

k k

i

2

ω

=

k k

i

=

T

=

n

Ts 2 + s 1

( + k k)

1

2

2

s + 2ξω s + ω

p

+ k k

+ k k

i

s 2 +

p

s + k k

i

n

n

T

T

Gdyby cały regulator PI był w torze głównym, to nie otrzymalibyśmy standardowej transmitancji 2-go rzędu

(nastąpiłaby zmiana w liczniku). Struktura rozdzielona jest preferowana przez praktyków dla uniknięcia przeregulowania (zob. dalej).

Uwaga.

Proste

serwomechanizmy

i

układy

automatyzacji

procesów

są

opisane

standardowymi transmitancjami 2-go rzędu.

Odpowiedź skokowa

1

W ( s) = s

2

ω

1

Y ( s

n

) =

⋅

s 2 + 2ξω s

2

+ ω s

n

n

∆ = 4 2 2

ξ ω n − 4 2

ω n = 4 2

ω ( 2

n ξ

− )

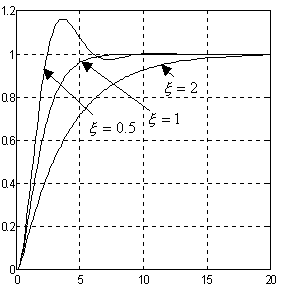
1

Kształt odpowiedzi zależy od współczynnika tłumienia ξ.

• ξ >1 ⇒

∆ >0

Dwa pierwiastki rzeczywiste różne: − s , − s 1

2

takie, że (− s ⋅ − s = ω

1 ) (

)

2

2

n

2

ω

1

R

R

R

n

0

1

2

Y ( s) =

=

+

+

( s + s )( s + s ) s

s

s + s

s + s

1

2

1

2

Residua R , R , R oblicza się metodą przesłaniania.

0

1

2

2

2

ω

ω

R =

n

= n = 1

0

(− s ) ( s )

2

ω

1

2

n

1

1

Oznaczmy

s =

, s =

1

T

2

T

1

2

1

2

 ω



(− s ) (− s )

s

T

T

1

2

2

2

1

R

n

= 



=

= −

= −

= −

1

 s( s + s )

− ( s ) ( s − s )

s − s

1

1

T − T

2

1

2

1

2

1

1

2

s = − s

−

1

T

T

2

1

Podobnie

T 2

R =

2

T − T

1

2

t

t

−

−

1

T

T

1

T

2

2

y( t) = 1

T

−

e

+

e

−

−

1

T

2

T

1

T

2

T

Jest to tzw. przebieg aperiodyczny zwykły.

• ξ =1 ⇒

∆ =0

Jeden pierwiastek podwójny: − s ,12 = ω n

2

ω

1

1

1

1

Y ( s

n

) =

=

,

= T ,

( s + ω )2 s

1

ω

2

s

n

(

s + )

1

n

ω n

1

1

Y ( s) = T

( s

)

1 2

+

s

Z tablic transformaty Laplace’a:

t

t

− T

y t

( ) = 1 − 1

( +

) e

T

Jest

to

przebieg

aperiodyczny

krytyczny.

Na

taki

przebieg

nastawia

się

serwomechanizmy.

• ξ <1 ⇒

∆ <0

Dwa pierwiastki zespolone:

s

1

,

,

1

= −ξω ± j

− 2

2

=

±

n

ω n

ξ

σ jω

gdzie

ω - częstotliwość drgań tłumionych

2

2

( s − s )( s − s ) = ( s − σ ) + ω

1

2

2

ω

1

Y ( s

n

) = ( s −σ)2

2

+ ω s

Typowy zapis:

R

C( s − σ ) + Sω

0

Y ( s) =

+

2

2

s

( s − σ ) + ω

2

2

ω

ω

=

n

R

= n = 1

0

2

2

2

σ + ω

ω n

Amplitudy S, C

Sω

⇒ Seσ t sin ω t

( s − σ )2 + ω 2

C( s − σ )

⇒ Ceσ t cosω t

( s − σ )2 + ω 2

Zachodzi wzór

1

2

2

1 ω 2

2

n

1

ω

S + jC =

[{( s−σ) +ω ] Y( s)}

= (

)

=

n

=

ω

s σ

jω

ω s

ω σ +

= +

jω

s =σ + jω

2

ω σ

ω

1

σ

ξω

n

− j

−

=

=

(σ − jω) =

− j =

n

− j =

2

ω σ + 2

2

ω

ω

ω

ω 1 ξ

n

−

−

=

ξ − j = S + jC

− 2

1 ξ

Zatem

−ξ

S =

,

C = 1

−

2

1 − ξ

Odpowiedź

y( t) = 1 + e t

σ ( S sin ω t + C cos t

ω )

Przekształcanie trygonometryczne

sin(α + β ) = sin α cos β + cosα sin β ,

gdzie α = t

ω

S

C

S sin ω t + C cosω t =

2

S +

2

C

(sin ω t

+ cosω t

) =

2

S + 2

2

C

S +

2

C

4

1

4

2

3

4

1

4

2

3

cos β

sin β

β ≡ φ

2

2

= S + C sin(ω t + φ)

sin β

C

1 − ξ 2

φ =

1

ar ctg

= ar ctg

=

,

2

2

S + C =

cos β

ar ctg

S

ξ

2

1 − ξ

1

ξ

− ω

(

y t ) = 1 −

e

t

n

sin(ω t + φ )

−ξ 2

1

Jest to przebieg oscylacyjny.

Matlab

omn=1

l=omn^2

% ξ >1

y

ksi=2

m=[1 2*ksi*omn omn^2]

t=0:0.1:20

y=step(l,m,t)

% ξ =1

ksi=1

m=[1 2*ksi*omn omn^2]

t=0:0.1:20

y1=step(l,m,t)

% ξ <1

ksi=0.5

m=[1 2*ksi*omn omn^2]

t=0:0.1:20

t

y2=step(l,m,t)

plot(t,y,t,y1,t,y2),grid

Uwaga.

Na lekko oscylacyjne przebiegi nastawia się układy automatyzacji procesów technologicznych (ciśnienie, poziom, przepływ) ze względu na dobre tłumienie zakłóceń.

5.2.

Ekstrema odpowiedzi oscylacyjnej

W celu wyznaczenia ekstremów odpowiedzi oscylacyjnej II rzędu można zastosować jedną z dwóch metod:

dy

-

policzenie pochodnej

w sposób tradycyjny i przyrównanie jej do zera (metoda

dt

często pracochłonna),

-

skorzystanie z właściwości transformaty Laplace’a, czyli z wzoru na transformatę pochodnej





2

1

 ω

ω

n



∂ y

ω

ω

1

= −

L [

2

s Y ( s)]

1

= −

L 

 = n eσ t sin ω t = 0

∂ t

( s − σ )2

2



+ω  ω





ω

π

t = π , π

2 , π

3 ...

ω =

=

i

,

t

i

i

π ,

t

i

i

ω

π

t =

i

i =

i

,

,

1 ,

2

.

3 ..

2

ω

−

n

1 ξ

π

π

t 1 =

=

ω 1

n

− ξ 2

ω

σ t

ω

ω

1

A = y(

1

1

t ) −1 = 1 + e

( S sin 1 t + C cos 1 t) =

=

σ

σ

σ

1 +

1

t

e

( S sinπ + C cosπ ) = −

1

t

C e

=

1

t

e

=

π

− ξ

2

π

1 ξ

−

= e

,

ponieważ σ = − ξω

t =

n ,

a

1

2

ω 1

n

−ξ

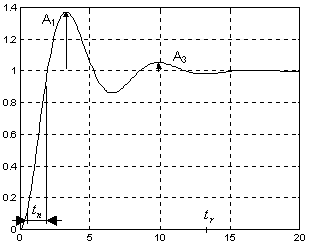
Parametry odpowiedzi oscylacyjnej:

-

przeregulowanie p% = A ⋅10 %

0

1

-

czas regulacji tr

-

czas narastania tn

A

-

stopień tłumienia

3

d = A 1

Przykład

ω n =1

ξ = 3

.

0

1

T =

= .

3 333

ξω n

tr ≈ 4 T = 13 3

. 32

• Przeregulowanie p%

πξ

−

2

−ξ

p% = A ⋅100%

1

= e

⋅100%

1

p%

ln 100

ξ =

p

2

2

%

π + ln 100

Zależ ność p%(ξ )

100

P%

90

80

Matlab

70

60

ksi=0.01:0.01:0.99;

50

p=exp(-pi*ksi./sqrt(1-ksi.*ksi))*100

40

plot(ksi,p),grid

30

20

10

00

0.2

0.4

0.6

0.8

1

ξ

Wzór przybliżony:

% ≈

ξ

p

1

( −

) ⋅100%

0 6

.

100

P%

90

Matlab

80

70

ksi=0.01:0.01:0.6

60

p=exp(-pi*ksi./sqrt(1-ksi.*ksi))*100

50

paproks=(1-ksi/0.6)*100

40

plot(ksi,p,ksi,paproks),grid

30

20

10

00

0.1

0.2

0.3

0.4

0.5

0.6

ξ

• Czas regulacji tr

t

t

− T

e

T

0.0

1.0

4

1.0

0.3679

t =

r 2% ξω n

2.0

0.1353

3.0

0.0495

≅5%

3

6

.

4

4.0

0.0183

≅2%

t =

,

t =

r

r

5% ξω

1% ξω

n

n

4.6

0.0100

1%

• Czas narastania tn

Od 10% do 90%

⇒

z wykresu można otrzymać przybliżony wzór:

.

1 8

t = ±

n

ω n

• Stopień tłumienia d

2πξ

ξω t

−

2

n 3

2

A

e

−ξ

 p% 

3

1

d =

=

= e

= 



ξω n 1

A

e

t

 100 

1

Tylko dla układu II rzędu stopień tłumienia jest kwadratem przeregulowania.

Uwaga. Technolodzy preferują małe d, aby oscylacje zanikały jak najszybciej.

Przykład.

Dla serwomachanizmu prądowego (zob. wcześniej) znaleźć k i α , gdy dane są: Tzam= 0.1, p% = 0.

p% oznacza ξ = 1 – przebiegi aperiodyczne krytyczne.

4

4

t

T

ω

r =

=

= 4 zam = 4

.

0

⇒

n = 10

ξω

ω

n

n

2

k

ω n

G

=

=

zam

2

2

2

s + k s

α + k s + 2ξω +ω

n

n

ξ

2 ω = α

k

,

2

k = ω

⇒ k = 100 , α = 0 2

.

n

n

Przykład.

Dobrać nastawy regulatora PI w układzie regulacji poziomu dla danych p% = 20%, tr = 0.5.

Zbiornik z wykładów 2, 3

k = k k = .

2 0

1

2

T = .

0 926 h

k k

i

2

T

ω n

G

=

=

zam

2

2

1 + k k

+ ξω + ω

p

k k

s

2

s

2

i

n

n

s +

s +

T

T

k , k

p

i = ?

p%

ln 100

ξ =

=

4

0 4

. 56 ,

t

ω

r =

.

0 5 =

⇒

n = 1 .

7 54

p

ξω

2

2

% 20%

π + ln

n

100

k k

1 + k k

2

ω = i

k

,

2

p

ξω =

⇒

k = 6 . 9

n

= 17 5

. 42

⇒

i = 142.5

T

n

T

p

k p

.

6 9

T =

=

= .

0 048 h = .

2 9 min = 174 s

i

k

14 .

2 5

i

5.3.

Wpływ dodatkowego zera i bieguna

• Wpływ zera

Układ regulacji poziomu ze standardowym regulatorem PI (nierozdzielonym) i

T = .

0 048



1 

k

k

1

p

+

ω





n = 1 .

7 54



T s

Ts + 1

i



ξ = 4

.

0 56

1

s +



1 

T

PI:

k

1 +

= k

i

p 







T s

p



s

i

kk p

s + 1/ T

k

i

T s

k

+1

p

k k s + 1/ T

p

(

i )

( i

)

TT

s

Ts + 1

i

G

=

=

=

zam

s + 1/ T

k

Ts 2 + s + kk s + 1/ T

1 + kk

kk

i

p (

i )

2

p

p

1 + k

+

+

p

s

s

s

Ts + 1

T

TTi

kk

1 + kk

p

2

= ω ,

p = ξ

2 ω

n

n

TT

T

i

2

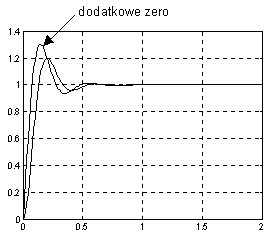
1 .

7 54 ( 0

.

0 48 s + )

1

G

- dodatkowe zero w liczniku

zam =

2

2

s + 2 ⋅ .

0 456 ⋅17 5

. 4 +1 .

7 54

Matlab

y

omn=17.54

ksi=0.456

l=omn^2

m=[1 2*ksi*omn omn^2]

standard

t=0:0.01:2

y=step(l,m,t)

Ti=0.048

% dodatkowe zero

l=conv(l,[Ti 1])

t

y1=step(l,m,t)

plot(t,y,t,y1), grid

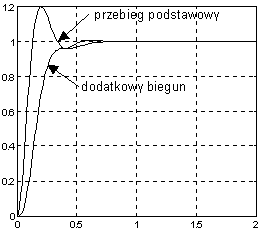
Jak widać przeregulowanie wzrosło (niekorzystne).

Uwaga.

Przez rozdzielenie PI na P+I, a PID na PI+D (ewentualnie I+PD) można uniknąć wprowadzania zer do licznika transmitancji układu zamkniętego, czyli nadmiernych przeregulowań.

• Wpływ bieguna

2

1

ω n

G

=

zam

2

2

Ts + 1 s + 2ξω s + ω

n

n

Matlab

y

omn=17.54

ksi=0.456

T=0.125

l=omn^2

m=[1 2*ksi*omn omn^2]

t=0:0.01:2

y=step(l,m,t)

% dodatkowy biegun

m=conv(m,[T 1])

y2=step(l,m,t)

plot(t,y,t,y2),grid

t

Uwaga. Pojawienie się dodatkowego bieguna powoduje wydłużenie czasu regulacji tr i zwiększenie czasu narastania t

(niekorzystne). Przeregulowanie znika

n

(korzystne).

5.4. Upraszczanie transmitancji wyższych rzędów Pytanie: Kiedy transmitancję wysokiego rzędu (np. 5-go) można zastąpić transmitancją 2-go rzędu?

• Odrzucanie dalekich biegunów i zer

Odrzucane pierwiastki muszą być przynajmniej 3 do 4 razy większe co do modułu od pozostawianych. Odrzucanie polega na wstawianiu zera zamiast s do odrzuconych czynników w celu zachowania wzmocnienia statycznego.

Przykład. Uprościć transmitancję

10( s + 10)

G( s) = 5

s + 5 4

s + 17 3

s + 43 2

s + 39 s + 27

Matlab

roots([1 5 17 43 39 27])

abs(roots([1 5 17 43 39 27]))

-0.5000 + 2.9580 i

3.0000

-0.5000 - 2.9580 i

3.0000

odrzucane

-3.0000

3.0000

-0.5000 + 0.8660 i

1.0000

-0.5000 - 0.8660 i

1.0000

1 (

0 s + 1 )

0

G( s) = [( s + )5

.

0

2 + .

2 9582 ] ( s + )

3 [( s + .

0 )

5 2 + .

0 8662 ]

Odrzucamy pierwiastki mianownika − 0.5 ± 2.95 i

8 , − 3 oraz – 10 z licznika.

Wstawienie s = 0 do odpowiednich wyrażeń:

1 (

0 0 +

G( s) ≅

1 )

0

=

[ 0

( +

)

5

.

0

2 + 9

.

2 582 ] (0 + )

3 [( s +

)

5

.

0

2 + .

0 8662 ]

100

100 / 27

=

=

32 ⋅ 3 ⋅[( s + .

0 )

5 2 + .

0 8662 ]

2

s + s + 1

y

Matlab

l=10*[1 10]

m=[1 5 17 43 39 27]

t=0:0.2:20

y=step(l,m,t)

l=100/27

m=[1 1 1]

y1=step(l,m,t)

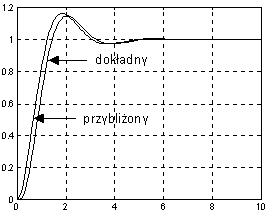
plot(t,y,t,y1),grid

t

Wniosek. Uproszczenie transmitancji „daje wyczucie” o ξ i ω n, czyli to, z jakim obiektem mamy do czynienia.

• „Redukcja” bardzo bliskich biegunów i zer

Maksymalna różnica pomiędzy redukowanymi pierwiastkami licznika i mianownika nie powinna przekraczać 15÷20%. „Redukcja” polega na wstawieniu s=0 do redukowanych czynników (zachowanie wzmocnienia statycznego).

Przykład. Uprościć transmitancję

297 (

5

. s + 2)

G( s) = 5

s + 15 7

. 5 4

s +137.5 3

s + 415 7

. 5 2

s + 712.5 s + 595

Matlab

roots([1 15.75 137.5 415.75 712.5 595])

abs(roots([1 15.75 137.5 415.75 712.5 595]))

-5.9911 + 7.0044i

9.2171

odrzucane

-5.9911 - 7.0044i

9.2171

-0.9754 + 1.7039i

1.9633

-0.9754 - 1.7039i

1.9633

-1.8171

1.8171

297 (

5

. s + )

2

G( s) = [( s + .59 )92 + 72][( s + 9.

0 7 )

5 2 + 7

.

1 2 ] ( s + .

1 8 )

2

( s + 2 ) jest bliskie ( s + 1 8

. 2 ) - redukcja

Stosujemy obydwa mechanizmy uproszczenia

297 (

5

. 0 +

G( s) ≅

)

2

=

[ 0

( + .

5 9 )

9 2 + 72 ] [( s + 9

.

0 7 )

5 2 + .

1 72 ] (0 + 8

.

1

)

2

29 .

7 5 ⋅ 2

.

3 85

=

=

2

.

9 22

8

.

1

(

2 2

s + .

1 95 s + .

2 7 )

5

( 2

s + 9

.

1 5 s + 8

.

3

)

4

Matlab

y

l=297.5*[1 2]

m=[1 15.75 137.5 415.75 712.5 595]

t=0:0.1:10

y=step(l,m,t)

l=297.5*2

m=9.22^2*1.82*[1 2*0.975 3.84]

y1=step(l,m,t)

plot(t,y,t,y1),grid

t

5.5.

Eliminacja przeregulowania przez filtrację wielkości zadanej



1



k

1

1

PID:

k

1 +

+ T s = k

p

+

+ k T s = k + k + k s

p 







T s

d

p



T s

p

d

p

i s

d

i

i

PID o podwójnym zerze równym 1:

( s + )

1 2

s 2 + 2 s + 1

2 s +1 + s 2

1

k

= k

= k

= k

2 + k

+ ks

s

s

s

s

Zatem:

kp = 2 k,

ki = k,

kd = k

Serwomechanizm z regulatorem PID o podwójnym zerze PID

( s

2

+ )

1

1

k

s

2

s

Pytanie. Dla jakiego k otrzymamy przebiegi aperiodyczne krytyczne?

( s + )2

1

1

k

2

s

k

s

( s + )2

1

Gzam =

( s + )

=

2

3

1

1

s + k( s + )2

1

1 + k

2

s

s

27

Odpowiedź . Przebiegi aperiodyczne krytyczne występują dla k =

(zob. linie pierwiastkowe)

4

3

27

s +

( s + )2 3 27 2 27 27

1

= s +

s +

s +

4

4

2

4

Matlab

roots([1 27/4 27/2 27/4])

27

2

-3.0000

( s + )1

-3.0000

4

Gzam = ( s + )32( s + 7.

0 5)

-0.7500

Sprawdzenie odpowiedzi

1.2

y

1

Matlab

0.8

l=27/4*[1 2 1]

m=[1 27/4 27/2 27/4]

0.6

t=0:0.05:5

0.4

y=step(l,m,t)

plot(t,y),grid

0.2

max(y)

00

1

2

3

4

5

t

y(max)=1.1789,

czyli p%=17.89%

Wniosek. Pomimo, że bieguny są rzeczywiste to przeregulowanie występuje ze względu na dwa zera w liczniku.

•

1

Filtrowanie przez inercję s +1

w

y

27 ( s + )1

Y ( s)

4

=

W ( s)

( s +3)2( s + .07 )5

1.2

Matlab

y

1

y 1

l=27/4*[1 2 1]

0.8

m=[1 27/4 27/2 27/4]

t=0:0.05:5

0.6

y=step(l,m,t)

0.4

l=27/4*[1 1]

y1=step(l,m,t)

0.2

plot(t,y,t,y1),grid

00

1

2

3

4

5

t

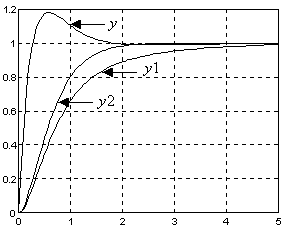
Dodanie filtru wielkości zadanej eliminuje przeregulowanie. Biegun filtru i zero regulatora są przeważnie wybierane jako takie same.

• Doprowadzenie do transmitancji II rzędu przez dobór specjalnego filtru Filtr

3

s +

4

4

(

- jednostkowe wzmocnienie statyczne filtru (koniecznie)

s

)12

+

3

G

(0)

filtr

= 1

w

4 s + .

0 75

7

.

6

(

5 s

2

+ )

1

1

y

2

3 ( s + )

1

2

s

s

27

Y ( s)

9

3

=

=

- wynikowy układ II rzędu

W ( s)

( s + 3)2 ( s + 3)2

Matlab

l=27/4*[1 2 1]

– bez filtru

y

m=[1 27/4 27/2 27/4]

t=0:0.05:5

y=step(l,m,t)

l=27/4*[1 1]

– z filtrem I rzędu

y1=step(l,m,t)

l=9

– ze specjalnym filtrem

m=[1 6 9]

y2=step(l,m,t)

plot(t,y,t,y1,t,y2),grid

t

Wniosek. Przez wstępną filtrację wielkości zadanej można ukształtować przebiegi dynamiczne w układzie.

Uwaga Na ogół dobrze jest, gdy odpowiedź na skok wielkości zadanej nie ma przeregulowania,

a

odpowiedź

na

zakłócenie

ma

lekkie

oscylacje.

Przeregulowanie eliminuje się stosując filtr wielkości zadanej lub podział

regulatora: PI=P+I, PID=PI+D (czasem I+PD).

5.6.

Stabilność układów ze sprzężeniem zwrotnym Definicja. Układ jest stabilny wtedy, gdy wszystkie bieguny układu zamkniętego są ujemne lub mają ujemne części rzeczywiste.

Pytanie. Jak zbadać stabilność nie obliczając pierwiastków?

• Kryterium stabilnoś ci Hurwitza

n 1

b

s −

−

+ ...+ b s + b

n 1

1

0

G

( s) =

,

an > 0

zam

n

n 1

a s + a

s −

−

+ ...+ a s + a

n

n 1

1

0

Lemat. Jeżeli wielomian

n

n 1

a s + a

s −

−

+ ... + a s + a

jest stabilny to jego wszystkie

n

n 1

1

0

współczynniki są dodatnie.

Uzasadnienie:

p < ,

0

p < 0 ,

p

gdzie σ < 0

... itd.

3,4 = σ + jω

1

2

2

2

a( s) = ( s − p

s

p

s σ

ω

s

p

s

p

s

σ

ω

1 ) (

− 2 )[( − ) + 2]... = ( + 1 ) ( + 2 )[( + ) + 2]... =

= n

s + ( p + p + 2σ ..

n−

s

+

1

2

). 1 ...

Wynika stąd, że wszystkie współczynniki jako sumy i iloczyny modułów będą dodatnie.

Twierdzenie Hurwitz’a

Dla wielomianu

n

n 1

a s + a

s −

−

+ ... + a s + a należy utworzyć następujący wyznacznik n× n: n

n 1

1

0

a

a

0

0

...

0

0

0

n 1

−

n

a

a

a

a

...

0

0

0

n−3

n−2

n 1

−

n

a

a

a

a

...

0

0

0

n−5

n−4

n−3

n−2

∆ =

n

...

...

...

...

...

...

...

...

0

0

0

0

... a

a

a

0

1

2

0

0

0

0

...

0

0

a 0

Następnie obliczamy podwyznaczniki ∆ , ∆ , ∆ , ..., ∆

. Jeżeli wszystkie podwyznaczniki

2

3

4

n 1

−

są dodatnie to wielomian jest stabilny.

Przykład. 3-ci rząd:

3

2

a s + a s + a s + a

3

2

1

0

Podwyznacznik

a

a

2

3

∆ =

= a a − a a

2

2

1

3

0

a

a

0

1

Układ 3-go rzędu jest stabilny, jeżeli iloczyn wyrazów środkowych jest większy niż iloczyn wyrazów skrajnych: a a > a a .

2

1

3

0

Przykład. Kiedy układ zamknięty o mianowniku 3

2

s + k( s + )

1

będzie stabilny?

s 3 + ks 2 + k

2 s + k

k

∆ =

1 = 2 k 2

2

− k

k

k

2

∆ = 2 2

k − k > 0 ,

k(2 k − )

1 > 0 ⇒ k > ,

0 k > 0 5

.

⇒

k > 0 5

.

2

Przykład. Dla jakich k następujący układ zamknięty będzie stabilny?

w

k

2

y

s

2

( Ts + )

1

k

2

Y ( s)

s T

( s + )

1 2

2 k

2 k

=

=

=

W ( s)

k

2

s T

( s + )

1 2 + k

2

T 2 s 3 + T

2 s 2 + s + 2 k

1 + s T

( s + )

1 2

Bada się stabilność mianownika, czyli

2

1

T

2 ⋅1 > 2 k ⋅ T

⇒

k < T

Uwaga. Kryterium Hurwitza jest wygodnie stosować dla układu 3-go rzędu i ewentualnie 4-go. Natomiast dla układów wyższych rzędów obliczanie wyznaczników staje się żmudne.

• Kryterium stabilnoś ci Routha

Twierdzenie Routha

Liczba pierwiastków wielomianu

n

n 1

a s + a

s −

−

+ ...+ a s + a , które mają dodatnie części n

n 1

1

0

rzeczywiste, jest równa liczbie zmian znaku w lewej skrajnej kolumnie następującej tablicy o n+1 wierszach:

s n

:

a

a

a

... 0

n

n−2

n−4

n 1

s − :

a

a

a

...

n 1

−

n−3

n−5

a

a

a

a

n

n−2

n

n−4

a

a

a

a

n−2

s

:

n 1

−

n−3

n 1

−

n−5

b =

b =

b

1

2

3

− a −

− a

n 1

n 1

−

a

a

a

a

n 1

−

n 3

−

n 1

−

n−5

b

b

b

b

n 3

s − :

1

2

1

3

c =

c =

1

2

− b

− b

1

1

...

...

0

s

:

Zatem:

-

Jeśli w pierwszej kolumnie są same „plusy” to wielomian jest stabilny

-

Jeśli znak w pierwszej kolumnie zmienia się raz, czyli mamy +/-, to jeden pierwiastek powoduje niestabilność

-

Jeśli znak w pierwszej kolumnie zmieni się dwa razy +/-/+ to dwa pierwiastki powodują niestabilność itd.

Twierdzenie Routha daje więcej informacji niż kryterium Hurwitza, ponieważ określa, ile pierwiastków powoduje niestabilność.

Przykład. Zbadać stabilność wielomianu

4

s + 2 3

s + 3 2

s + 4 s + 5

4

s :

1

3

5

0

3

s :

2

4

0

W pierwszej kolumnie występują

2

dwie zmiany znaku +/-/+ co oznacza,

s :

1

5

0

1

że dwa pierwiastki powodują niestabilność.

s :

− 6 0

0

s :

5

Matlab

roots([1 2 3 4 5])

0.2878 + 1.4161 i

- niestabilność

0.2878 - 1.4161 i

- niestabilność

-1.2878 + 0.8579 i

-1.2878 - 0.8579 i

Pytanie. Co zrobić, kiedy w pierwszej kolumnie pojawi się zero?

Przypadek I

Jeśli wiersz poza zerem na początku ma przynajmniej jeden niezerowy składnik, to zero w lewej kolumnie zastępuje się przez małą liczbę ε i kontynuuje budowę tablicy. Na końcu lub na bieżąco analizuje się znaki przy ε → 0 .

Przykład. Zbadać stabilność wielomianu

4

3

s + s + 2 2

s + 2 s +1

4

s :

1

2

1

0



1 

3

Granica lim 2 −  = −∞ ,

s :

1

2

0

ε →0

ε 

2

s :

/,

0 ε

1

0

co oznacza, że występują

1

1

dwie zmiany znaku,

s :

2 −

0

ε

czyli układ jest niestabilny.

0

s :

1

Matlab

roots([1 1 2 2 1])

0 1

. 217 ±1.306 i

6

- niestabilność

− 0.6217 ±1 4

. 40 i

6

Przypadek II

Jeśli wiersz zawiera same zera, to korzystamy z wyrazów w poprzednim wierszu budując wielomian pomocniczy odpowiedniego stopnia. Następnie różniczkujemy ten wielomian, współczynniki pochodnej wpisujemy zamiast zerowego wiersza i kontynuujemy procedurę.

Wielomian pomocniczy jest podzielnikiem wielomianu głównego, zatem jego pierwiastki są pierwiastkami wielomianu głównego i na ogół można je obliczyć. Wielomian główny nie jest stabilny (niestabilny lub na granicy stabilności).

Przykład. Zbadać stabilność wielomianu

5

s + 2 4

s + 3 3

s + 6 2

s − 4 s − 8

5

s :

1

3

− 4 0

4

s :

2

6

− 8 0

3

s :

0/

0/

0/

a pom = 2 4

s + 6 2

s − 8

8

12

0

da pom

2

s :

3

−8 0

= 8 s 3 +12 s

ds

100

1

s :

0

3

pierwiastki a

2

s =

s = −

pom:

,

1

2

4

0

s :

− 8

stąd

s = 1 ,

s = −1 , s = i

2 ,

s = − i

2

1

2

3

4

Matlab

roots([1 2 3 6 -4 -8])

±2 i

- 2

- 1

- 1

- niestabilny