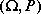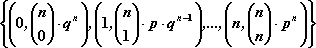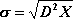
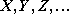
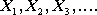
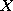
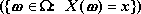
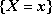
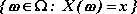
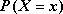
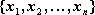
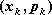
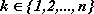
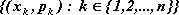
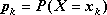
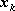
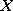
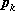
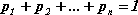
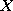
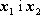
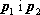
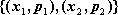
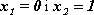
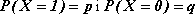
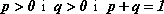
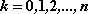
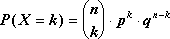
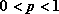
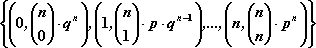
Edukator.pl - serwis edukacyjny http://www.edukator.pl/index.php?page=790

Zmienna losowa

Bardzo często ze zdarzeniami losowymi wiąże się pewne wielkości liczbowe.

Niech para

będzie przestrzenią probabilistyczną.

Każdą funkcję określoną na zbiorze skończonym o wartościach rzeczywistych nazywamy zmienną losową przestrzeni probabilistycznej

, krótko zmienną losową.

Zmienne losowe będziemy oznaczać literami lub

Zdarzenie - zmienna losowa przyjmuje wartość

oznaczać będziemy symbolem:

, a

prawdopodobieństwo zdarzenia symbolem

.

Zmienną losową skokową nazywamy zmienną losową, która ma skończony lub przeliczalny zbiór wartości.

Rozkład zmiennej losowej skokowej.

Dana jest zmienna losowa, której zbiorem wartości jest zbiór:

. Zbiór wszystkich uporządkowanych par postaci dla

, a więc zbiór:

, gdzie

jest

prawdopodobieństwem, z jakim zmienna losowa przyjmuje wartość

, nazywamy rozkładem zmiennej losowej

.

Prawdopodobieństwa

spełniają zależność:

.

Zatem rozkład zmiennej losowej to zbiór uporządkowanych par, w których pierwszym elementem jest wartość zmiennej losowej

, a drugim jest prawdopodobieństwo, z jakim wartość ta jest przyjmowana przez zmienną losową

.

Jeżeli zmienna losowa przyjmuje tylko dwie wartości z prawdopodobieństwami odpowiednio

, to zbiór

nazywamy rozkładem dwupunktowym.

Gdy

oraz

(

), to zbiór

nazywamy rozkładem zerojedynkowym.

Jeżeli zmienna losowa przyjmuje wartości z prawdopodobieństwami

, gdzie

i

, to zbiór:

1 z 3

2007-10-09 22:52

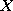
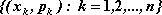
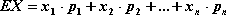
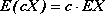
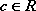
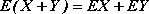
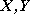
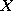
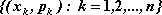
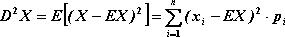
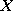
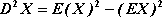
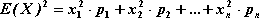
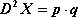
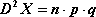
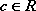
Edukator.pl - serwis edukacyjny http://www.edukator.pl/index.php?page=790

nazywamy rozkładem dwumianowym (Bernoulliego).

Jeżeli zmienna losowa przybiera wszystkie swoje wartości z takim samym prawdopodobieństwem, to mówimy, że ma ona rozkład jednostajny.

Wartość oczekiwana zmiennej losowej.

Wartością oczekiwaną (wartością średnią, wartością przeciętną, nadzieją matematyczną) zmiennej losowej o rozkładzie

nazywamy liczbę:

.

Własności wartości oczekiwanej.

1.

, gdzie

2.

, gdzie

- zmienne losowe określone na tym samym zbiorze zdarzeń elementarnych

.

Wariancja zmiennej losowej.

Wariancją zmiennej losowej o rozkładzie

nazywamy liczbę:

,

gdzie

jest wartością oczekiwaną zmiennej losowej

.

Wariancję zmiennej losowej można też obliczyć ze wzoru:

, gdzie

.

Wariancja zmiennej losowej jest parametrem charakteryzującym rozrzut wartości zmiennej losowej względem wartości oczekiwanej.

Zawiera informację o tym, jak daleko od wartości oczekiwanej znajdują się wartości zmiennej losowej. Jeśli

, to oznacza, że

zmienna losowa jest funkcją stałą o wartości równej wartości oczekiwanej

.

Wariancje zmiennej losowej w niektórych rozkładach: 1. Rozkład dwupunktowy -

.

2. Rozkład dwumianowy -

.

Własności wariancji

1. Wariancja jest liczbą nieujemną.

2.

, gdzie

.

2 z 3

2007-10-09 22:52

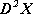
Edukator.pl - serwis edukacyjny http://www.edukator.pl/index.php?page=790

Odchylenie standardowe zmiennej losowej Liczbę

, gdzie

jest wariancją zmiennej losowej

, nazywamy odchyleniem standardowym zmiennej losowej

.

3 z 3

2007-10-09 22:52