POLE GRAWITACYJNE

→

m m

r

F = − ⋅ 1 2 ⋅

g

G

r 2

r

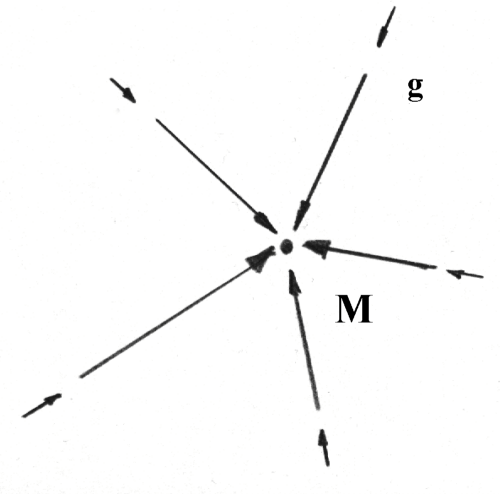
Natężenie pola

F

K

g

=

=

g

K

g

m

g

GM r

g = −

⋅

r 2

r

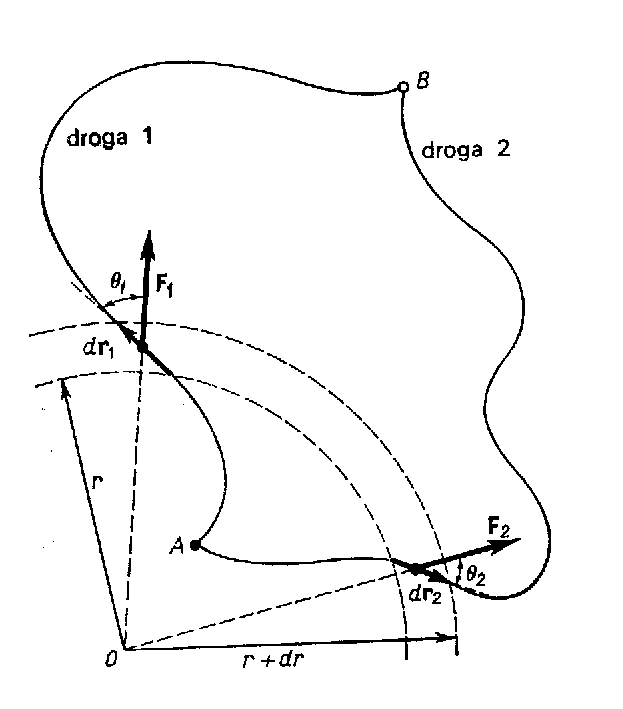
Pole grawitacyjne jest polem zachowawczym :

dW =

s

d

F

= Fds ⋅ cosα

ds ⋅ cos α = dr dW = Fdr = F ⋅ r d

w górę

dWg = - F(r)dr

w dół

dWd = F(r)dr

∫ Fdr = 0

1

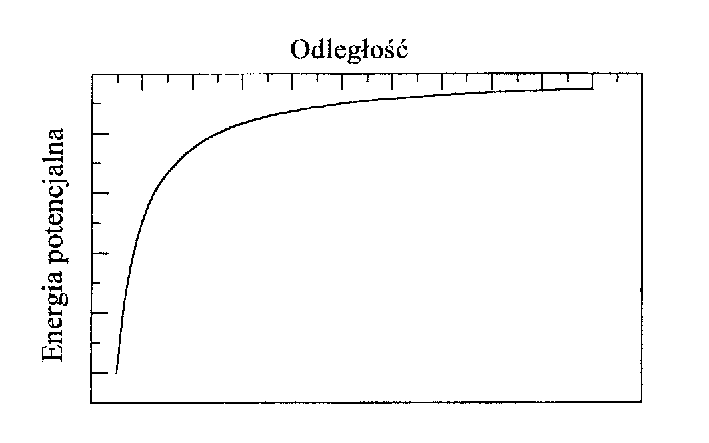
ENERGIA GRAWITACYJNA

Energia potencjalna

∞

V ( r)

r

= ∫ F dr

F dr

g

= ∫ z

r

∞

GMm r

F = − F

F =

z

g z

r 2

r

B





V ( )

GMm

r = −

∫ 1 dr = 

− 1 − 1 

r

bo r 2

 r

r

B



A

A

Pole energii potencjalnej jest polem skalarnym.

Energia potencjalna jest addytywna:

F = F

F

1 +

2 + ... ⇒ V = V1 + V 2 + ...

γ ( r)

GM

potencjał grawitacyjny

= − r

2

ENERGIA GRAWITACYJNA BLISKO POWIERZCHNI ZIEMI

GMm

V = − R + h Z

GMm 

1



GMm 

h 

V = −



 ≈ −

1 −



R

1 h / R

R

R

Z

 +

Z 

Z



Z 

1

≈ 1− x

dla x<<1 1+ x GMm

V = −

2

( R − h = 0 +

Z

) V mgh

RZ

Ep ≈ mgh

3