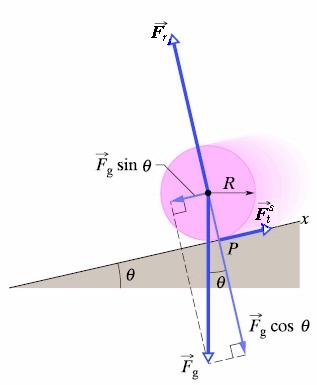
Staczanie bez poślizgu ciała o symetrii osiowej z równi pochyłej siła tarcia (statycznego) ma zwrot w górę równi

– zapobiega poślizgowi

kierunek w dół równi przyjmujemy za dodatni równanie ruchu postępowego:

||

s

F = F − F

w

g

t

s

m a = m g sin θ − Ft (1)

można wykorzystać równanie ruchu obrotowego zarówno w układzie odniesienia związanym ze środkiem masy ( A) jak i w układzie odniesienia związanym z chwilowym punktem styczności z podłożem ( B); w obu przypadkach wypadkowy moment siły pochodzi tylko od jednej z występujących sił:

s

.

A

I ε

0

= τ =

s

RF

F

t

t

B. I

=

=

Pε

τ || Rmg s

F

θ

in

g

zwrot wektora τ r przed płaszczyznę rysunku powoduje obrót przeciwnie do wskazówek zegara, tzn. ruch szpulki w dół równi a

toczenie bez poślizgu – zachodzi zależność a = ε R

→ ε =

R

a

s

.

A

I 0

= RFt

(2 A)

R

a

B. (

2

I + mR )

= R m g s

0

θ

in

(2 B)

R

A. ruch obrotowy wokół osi przechodzącej przez środek masy z (1) obliczamy F st i podstawiamy do (2 A): F s = m g sin θ − m a t

(3 A)

a

I

= R( mg sin θ − ma) 0

/ ⋅ R

R

I a = mR 2 g sin θ − m R 2 a 0

porządkujemy ostatnie równanie ze względu na a a (

2

I + m R )

2

= mR g sin

0

θ

2

mR

a =

g s θ

in

2

I + m R

(4 A)

0

obliczenie F st – podstawiamy (4 A) do (3 A) 2

mR

F s = mg sin θ − m a = mg sin θ − m g sin θ =

t

2

I + m R

0

2

2

I mg sin θ + m R mg sin θ − m R mg sin θ

0

=

2

I + m R

0

I 0

F s =

mg sin

t

θ

2

I + m R

(5 A)

0

B. ruch obrotowy wokół osi przechodzącej przez chwilowy punkt styczności z podłożem z (2 B) obliczamy a i podstawiamy do (1): 2

m R

a =

g sin θ

2

I + mR

(4 B)

0

m R 2

s

sin θ =

sin θ −

m

g

m g

Ft

I + mR 2

0

2

2

2

m R

I + mR − m R

F s = m g sin −

=

t

θ m

g sin θ

0

m g sin θ

2

2

I + mR

I + mR

0

0

I 0

F s =

mg s

t

θ

in

2

I + m R

(5 B)

0

równania (4 A) i (4 B) oraz (5 A) i (5 B) są identyczne – rozważenie ruchu obrotowego w dwóch układach odniesienia: związanym ze środkiem masy i związanym z chwilowym punktem styczności z podłożem daje takie same wyniki jeżeli ciało jest jednorodne lub puste w środku – I 0 = β mR 2

2

m R

a =

g sin θ

β

2

2

mR + mR

1

a =

g

θ

β

sin

+1

(4)

β

2

mR

F s =

m g s

t

θ

in

β

2

2

mR + m R

β

F s =

m g sin

t

θ

β +1

(5)