X jest zmienna losową o gęstości 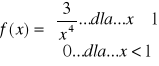
. Należy obliczyć EX, ![]()
. I tak:
Dzis wykonamy jedno z zadań domowych, jakie było zadane do rozwiązania na popraednich ćwiczeniach. A jest to zadanie 4.68.
X jest zmienna losową o gęstości 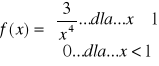
. Należy obliczyć EX, ![]()
. I tak:
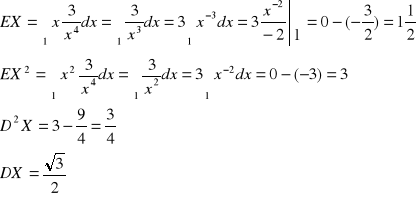
Przejdźmy teraz do naszego dzisiejszego tematu jakim sa podstawowe rozkłady prawdopodobieństwa. Wykonajmy takie zadanie. Próbujemy niezależnie 5 razy połączyć się z serwerem poczty elektronicznej. Prawdopodobieństwo połączenia w jednej próbie wynosi 0,8. X to liczba połączeń. Należy wyznaczyć prawdopodobieństwo, że z serwerem połączymy się 4 razy, najwyżej 3 razy i przypadek trzeci do domu: co najmniej 3 razy. Rozpatrzmy przypadek pierwszy:
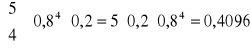
I przypadek drugi: 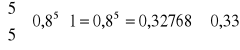
. Stąd mamy:
![]()
, gdzie X to liczba połączeń, a n jest równe 5 i p jest równe 0,8.
Kolejne zadanie. Prawdopodobieństwo wygrania nagrody na loterii wynosi 0,003. Korzystając z przybliżenia Poissona należy wyznaczyć prawdopodobieństwo, że wśród 500 osób grających na loterii:
Żadna nie wygra.
Wygrają 2 osoby.
Wygra najwyżej 5 osób.
Wygrają co najmniej 3 osoby.
Wygra 0,6 % grających.
Przypadek d i e zostawiamy do domu, natomiast teraz rozpatrzymy trzy pierwsze. I tak wiemy, że p = 0,003, oraz n = 500. Mamy:
By wyliczyć P(X=0) korzystamy z wzoru ![]()
i z tabeli rozkładu Poissona odczytujemy, że P(X=0) = 0,2231.
Z tabeli można odczytać automatycznie, że P(X=2) = 0,251.
W tym przypadku jest podobnie. ![]()
.
Kolejne zadanie. Tym razem z rozkładu normalnego. Zmianna losowa X ma rozkład N(-2;3). Obliczyć:
P(X>-1)
P(X<-5)
P(-5<X<-1)
Otrzymane wyniki zinterpretować na wykresie gęstości. I tak:
Skorzystamy ze wzoru ![]()
. A zatem: ![]()
![]()
. Dla ujemnych stosujemy bowiem zawsze przelicznik: ![]()
.
![]()
![]()
Nastepne zadanie z rozkładu normalnego. Reklama cukierków TIK TAK zapewnia, że mają one tylko 2 kalorie. Jak duże powinno być odchylenie standardowe rozkładu kaloryczności tych cukierków, aby szansa trafienia na cukierek zawierający co najmniej 3 kalorie była mniejsza niż 0,01 (przyjmujemy rozkład normalny N(![]()
)). A więc mamy dane, że X to kalorycznośc równa N(![]()
)). Szukamy prawdopodobieństwa, że ![]()
. A zatem liczymy:
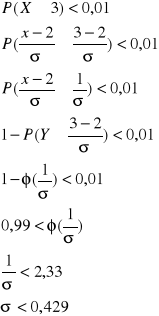
I mamy obliczone. Wartośc 2,33 została odczytana z tablicy rozkładu normalnego. To tyle jeśli chodzi o zadania. Na zakończenie należy wykonać w domu zadanie 4.92 z książki Statystyka autorstwa Lucjana Kowalskiego, oraz zadanie 4.91 - przykłady a, b i c.