Zadanie III 20 Term 2009 Agnieszka Ziemińska P-51 [e-mail]

W eksplozji termojądrowej temperatura wybuchu wewnątrz kuli ognistej osiąga chwilową wartość T_k=10⁷ [K] Oblicz długość fali λ_MAX dla której funkcja rozkładu widmowego objętościowej gęstości zasobu energii promieniowania ρ_T(λ) osiąga wartość maksymalną oraz wartość objętościowej gęstości zasobu energii promieniowania ε_IV i ciśnienie promieniowania p wewnątrz kuli ognistej. Stała Boltzmanna k= 1,3806·10^-23 [
], stała Plancka

h=6,6262*10^-34 [Js], stała Wiena
, prędkość światła w próżni
.

1. Wyznaczenie funkcji rozkładu widmowego objętościowej gęstości zasobu energii promieniowania.

Średni zasób energii promieniowania w przedziale całego pola dozwolonych stanów energetycznych (stopni swobody) ma postać:

- w funkcji długości fali

- w funkcji częstotliwości

Elementarny przyrost objętościowej gęstości zasobu ilości oscylatorów w przedziale długości fal od λ do λ+dλ określony jest zależnością:

gdzie funkcja rozkładu widmowego objętościowej gęstości zasobu ilości oscylatorów w polu długości fal określona jest związkiem:

Uwzględniając związek między długością fali elektromagnetycznej a jej częstotliwością w próżni:

otrzymano elementarny przyrost objętościowej gęstości zasobu ilości oscylatorów w przedziale częstotliwości fal od
+d

gdzie funkcja rozkładu widmowego objętościowej gęstości zasobu ilości oscylatorów w polu częstotliwości fal określona jest związkiem:

Objętościowa gęstość zasobu ilości oscylatorów jest równa:

Funkcja rozkładu widmowego objętościowej gęstości zasobu energii promieniowania w polu długości fal określona jest zależnością:

zaś funkcja rozkładu widmowego objętościowej gęstości zasobu energii promieniowania w polu częstotliwości fal jest równa:

2. Wyznaczenie objętościowej gęstości zasobu energii promieniowania

Całka z funkcji rozkładu widmowego objętościowej gęstości zasobu energii promieniowania określa objętościową gęstość zasobu energii promieniowania.

Przyjmując oznaczenie

otrzymano

3. Wyznaczenie maksimum funkcji rozkładu widmowego objętościowej gęstości zasobu energii promieniowania.

Funkcja rozkładu widmowego objętościowej gęstości zasobu energii promieniowania w polu długości fal określona jest zależnością:

Przyrównując pochodną funkcji po długości fali do zera:

otrzymano równanie

Przyjmując oznaczenie:

powyższe równanie przyjmuje postać:

z którego wyznaczono wartość

x = 4,965

dla tej wartości x funkcja rozkładu widmowego objętościowej gęstości zasobu energii promieniowania osiąga maksimum zaś długość fali osiąga wartość:

4. Prawo przesunięć Wiena

Uwzględniając wyrażenie

dla x = 4,965

otrzymano

Stąd

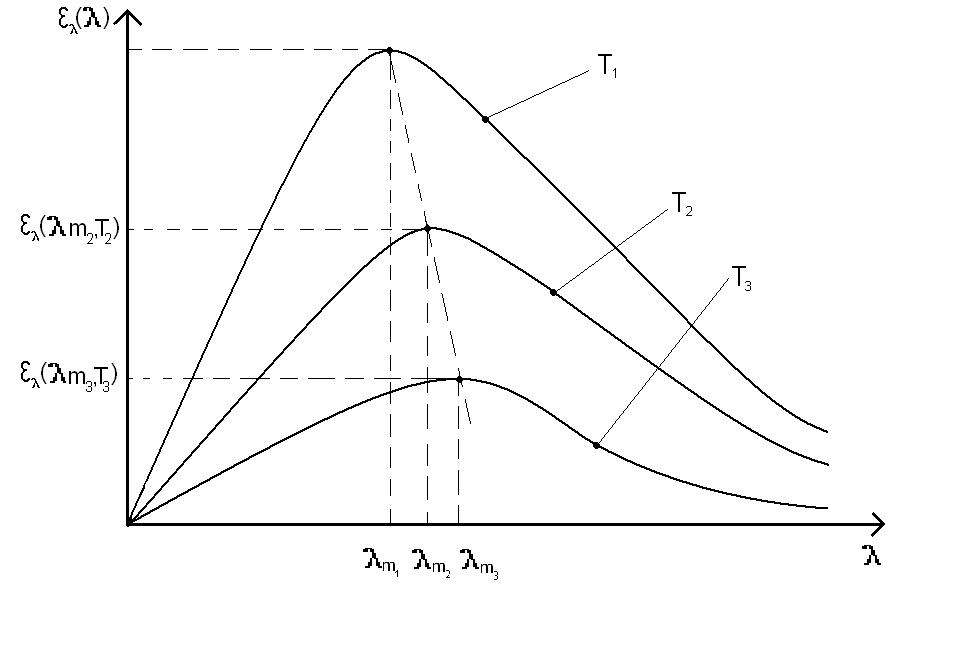
Powyższa zależność definiuje prawo przesunięć Wiena które głosi, że odwrotnie proporcjonalna zależność długości fal
od temperatury T opisuje ilościowo mechanizm przesuwania się maksimum funkcji rozkładu widmowego objętościowej gęstości zasobu energii promieniowania
w miarę wzrostu temperatury w stronę fal krótszych.

5. Wyznaczenie ciśnienia promieniowania

Relacja między unoszoną przez foton energia h
a masą fotonu zgodnie kwantową hipotezą Plancha i relatywistyczną zależnością Einsteina określona jest związkiem

stąd masa fotonu

Przyrównując fotony do cząsteczek gazu można przystosować wyrażenie określające ciśnienie cząsteczek gazu

do określenia ciśnienia promieniowanie

gdzie
- średnia masa fotonu

Funkcja rozkładu zasobu energii promieniowania
w polu dozwolonych stanów energetycznych równa jest iloczynowi dozwolonego stanu energetycznego
i funkcji rozkładu prawdopodobieństwa zdarzenia losowego
aż oscylator promieniowania długości fali λ zajmie dozwolony stan energetyczny

gdzie
jest określona czynnikiem Boltzmanna

Średni zasób energii oscylatora promieniowanie (fotonu)
o częstotliwości ν dla wszystkich stanów energetycznych jest równy

Zatem funkcja rozkładu widmowego objętościowej gęstości zasobu energii promieniowania określona jest związkiem

=
·
=

zaś objętościowa gęstość zasobu energii wewnętrznej fotonów w pudle izotermicznym określona jest wyrażeniem

Całka z funkcji rozkładu widmowego objętościowej gęstości zasobu ilości fotonów w pudle izotermicznym po wszystkich długościach fal

równa jest objętościowej gęstości zasobu ilości fotonów.

Zatem objętościowa gęstość zasobu energii wewnętrznej fotonów w pudle izotermicznym przyjmie postać

Podstawiając otrzymamy wynik do wyrażenia określającego ciśnienie promieniowania uzyskano równanie

które jest równaniem stanu gazu fotonowego

6. Obliczenie wartości długości fali
dla której funkcja rozkładu widmowego objętościowej gęstości zasobu energii promieniowanie osiąga maksimum.

Z prawa przesunięć Wiena określono

=

7. Obliczenie wartości objętościowej gęstości zasobu energii wewnętrznej promieniowania

=β
₌

_{8. Obliczenie wartości ciśnienia promieniowania wewnątrz kuli ognistej}

p=

=

---