Zadanie 1.2.

Udowodnić, że prawdopodobieństwo zdarzenia A jest równe P(A) = 1 - P(A'), gdzie A' jest zdarzeniem przeciwnym do A.

c.n.u.

Zadanie 1.3.

Udowodnić twierdzenie: Prawdopodobieństwo alternatywy dowolnych zdarzeń A i B dane jest wzorem:
.

... (1)

... (2)

Z (1) i (2) mamy:

c.n.u.

Zadanie 1.4.

Z dobrze potasowanej 52-kartowej talii wyciągamy w sposób losowy 26 kart. Jakie jest prawdopodobieństwo, że wśród wyciągniętych kart będzie połowa czerwonych i połowa czarnych kart?

ROZWIĄZANIE

Ω - przestrzeń zdarzeń elementarnych,

ω - elementy przestrzeni Ω

A - zdarzenie,

Z definicji klasycznej:

Odp.: Prawdopodobieństwo, że wśród wyciągniętych kart będzie połowa czarnych i polowa czerwonych wynosi w przybliżeniu 0,218.

Zadanie 1.5.

Przypuśćmy, że z urny zawierającej 49 losów ponumerowanych liczbami od 1 do 49 wyciąga się 6 losów (toto-lotek). Obywatel X wypełnił tylko jeden mały kupon. Jakie jest prawdopodobieństwo zdarzenia A polegającego na tym, że w

najbliższym losowaniu zostaną wylosowane dokładnie te same numery, które skreślił obywatel X ? Jakie jest prawdopodobieństwo zdarzenia B polegającego na tym, że w najbliższym losowaniu zostanie wylosowanych co najmniej

pięć numerów spośród numerów skreślonych przez obywatela X .

ROZWIĄZANIE

Z definicji klasycznej:

• 
  ,bo
  

• 
  B_i- trafiono i liczb

B₆=A

Odp.: Prawdopodobieństwo wylosowania pięciu numerów z pośród skreślen obywatela X wynosi

Zadanie 1.6.

Oznaczmy:

A - orzeł w pierwszym rzucie

P(A) - prawdopodobieństwo wynosi 1/2

B - orzeł w drugim rzucie

P(B) - prawdopodobieństwo wynosi 1/2

Co najmniej jeden orzeł w dwóch rzutach, więc alternatywa zdarzeń A i B. AUB

Prawdopodobieństwo wynosi P(AUB)

Korzystając ze wzoru udowodnionego w zadaniu 1.3

P(AUB)=P(A)+P(B)-P(A∩B)

I wzoru na iloczyn prawdopodobieństw

P(A∩B)=P(A)*P(B)

Otrzymujemy

P(AUB)=P(A)+P(B)-P(A)*P(B)

1/2 + 1/2 - 1/2 * 1/2 = 3/4

Zadanie 1.7.

Z - rzucamy parzystą ilość razy, aż dwa razy pod rząd wypadnie ta sama strona monety. Nie liczy się to, co wypadnie pierwsze orzeł czy reszka. Ważny jest czy kolejny rzut będzie taki sam jak poprzedni.

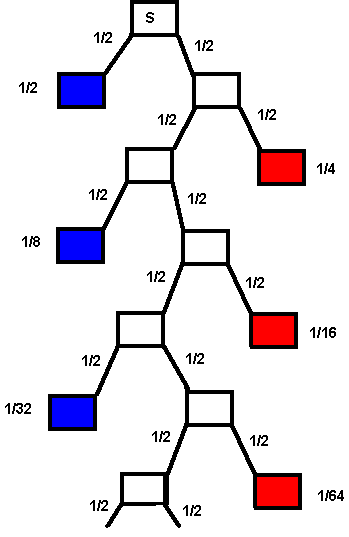
Drugi rzut. Pierwsza szansa parzystego zakończenia losowania

Czwarty rzut. Druga szansa parzystego zakończenia losowania

Szósty rzut. Trzecia szansa parzystego zakończenia losowania

Ósmy rzut. Czwarta szansa parzystego zakończenia losowania

P(Z)- suma wszystkich szans zdarzeń sprzyjających, ścieżka kończy się na niebiesko.

Jest to suma nieskończona.

P(Z)=1/2+1/8+1/32+…

Łatwo zauważyć, że jest to ciąg geometryczny. Korzystając z odpowiedniego wzoru.

a_z=1/2 q_z=1/4 S_z=a_z/(1-q_z) S_z=(1/2)/(1-1/4)=(1/2)/(3/4)=2/3

Zdarzenie przeciwne N rzucamy nieparzystą ilość razy, Ścieżka zakończona na czerwono.

P(N)=1/4+1/16+1/64+…

an=1/4 qn=1/4 Sn=an/(1-qn) Sn=(1/4)/(1-1/4)=(1/4)/(3/4)=1/3

P(Z)+P(N)=2/3+1/3=1

Zadanie 1.8.

Oznaczmy co jest uszkodzone:

A - układ kierowniczy

B - układ hamulcowy

C - układ napędowy

A∩B - układ kierowniczy i układ hamulcowy

A∩C - układ kierowniczy i układ napędowy

B∩C - układ hamulcowy i układ napędowy

P(A) = 40%

P(B) = 45%

P(C) = 60%

P(A∩B) = 15%

P(A∩C) = 15%

P(B∩C) = 20%

Cel: Znaleźć ile procent samochodów ma zepsute wszystkie trzy układy A∩B∩C

Ponieważ dobrego samochodu się nie naprawia.

P(AUBUC)=100%

Korzystając ze wzoru udowodnionego w zadaniu 1.3

P(AUB)=P(A)+P(B)-P(A∩B)

Wyprowadźmy wzór na alternatywę trzech zdarzeń

P(AUBUC)=
P(AU(BUC))=
P(A)+P(BUC)-P(A∩(BUC))=
P(A)+P(BUC)- P((A∩B)U(A∩C))=
P(A)+P(B)+P(C)-P(B∩C)-(P(A∩B)+P(A∩C)-P((A∩B) ∩ (A∩C)))=

P(A)+P(B)+P(C)-P(B∩C)-P(A∩B)-P(A∩C)+P(A∩B∩C)

P(AUBUC)=P(A)+P(B)+P(C)-P(B∩C)-P(A∩B)-P(A∩C)+P(A∩B∩C)

P(A∩B∩C)=P(AUBUC)-P(A)-P(B)-P(C)+P(B∩C)+P(A∩B)+P(A∩C)

Podstawmy i obliczmy

P(A∩B∩C)=100% - 40% - 45% - 60% + 20% + 15% + 15% = 5%

---