Wydział Inżynierii Lądowej	Dzień/godzina Poniedziałek, 11:15-14:00		Nr zespołu 24
		Data: 7.12.2009
Nazwisko i imię: Basaj Radosław Filipek Dawid Horbowicz Marcin	Ocena z przygotowania	Ocena ze sprawozdania	Ocena

Temat: Pomiar długości fal elektromagnetycznych metodami interferencyjnymi.

Podstawowe wiadomości.

Fala elektromagnetyczna to rozchodzące się w przestrzeni okresowe zmiany pola elektrycznego i magnetycznego. Wektory natężenia pola elektrycznego i indukcji magnetycznej fali elektromagnetycznej są do siebie prostopadłe i leża w jednej płaszczyźnie, która jest prostopadła do kierunku rozchodzenia się fali. Fale elektromagnetyczne o różnych częstotliwościach, a co za tym idzie , również różnych długościach wchodzą w skład widma elektromagnetycznego.

Do wyróżnionych przedziałów widma elektromagnetycznego należą :

• fale radiowe:

- długie (1000-2000m)

- średnie (200-600m)

- krótkie (10-75m)

- ultrakrótkie (1-10m)

• mikrofale (1mm-1m)

• promieniowanie podczerwone (0,7µm-1mm)

• światło widzialne (0,4µm-0,7µm)

• promieniowanie nadfioletowe (0,4µm-10µm)

• promieniowanie X (0,001-10nm)

• promieniowanie gamma (<0,1nm)

Interferencja jest to zjawisko nakładania się na siebie dwóch lub więcej ciągów falowych w danym punkcie przestrzeni, w wyniku którego, fale ulegają wzmocnieniu lub osłabieniu, a nawet dochodzi do całkowitego wygaszenia.

Obraz interferencyjny możemy zaobserwować wówczas, gdy:

• źródła są monochromatyczne (wysyłają fale o jednakowej długości)

• źródła interferujących fal są spójne tzn. fale wysyłane przez te źródła zachowują stałą w czasie różnicę faz.

Wzmocnienie drgań cząsteczek ośrodka(maksimum interferencyjne) otrzymamy gdy różnica dróg optycznych dwóch fal jest równa całkowitej wielokrotności długości fali: Δ=m λ

Osłabienie zaś gdy różnica dróg optycznych wynosi:

Δ=(2m+1) λ/2

Zasada działania interferometru Michelsona:

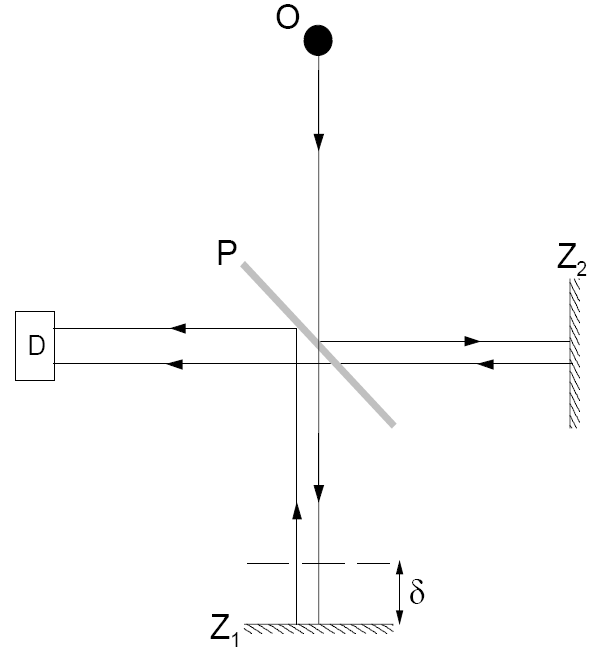
Rys.1. Schemat układu pomiarowego z interferometrem Michelsona. O - źródło fal elektromagnetycznych, P - płytka półprzepuszczalna, Z₁ i Z₂ - zwierciadła, D - detektor fal elektromagnetycznych, δ - linijka

Wiązka fal elektromagnetycznych ze źródła pada na płytkę płasko równoległą, która przepuszcza połowę natężenia fali, a drugą połowę odbija. Wiązka przechodząca pada na prostopadłe do jej kierunku zwierciadła. Po odbiciu wraca tą samą drogą, odbija się od płytki i pada na detektor. Wiązka odbita pierwotnie od płytki pada prostopadle na zwierciadło wraca po odbiciu ta samą drogą, przechodzi przez płytkę i spotyka się z wiązką pierwszą w detektorze. Na skutek występowania różnicy dróg optycznych obu wiązek powstają prążki interferencyjne. Interferencja powstaje w obszarze, w którym obie wiązki biegną razem w stronę detektora. Przesuwając zwierciadło zmieniamy długość drogi optycznej wiązki odbijającej się od niego, a więc różnicę dróg obu wiązek. Detektor zarejestruje przesuwanie się prążków interferencyjnych. Jeśli w środku obrazu jedno maksymalne wzmocnienie zostanie zastąpione przez kolejne maksymalne wzmocnienie, oznacza to, że różnica dróg wiązek zmieniła się o jedną długość fali.

Zasada działania interferometru Fabry - Perota:

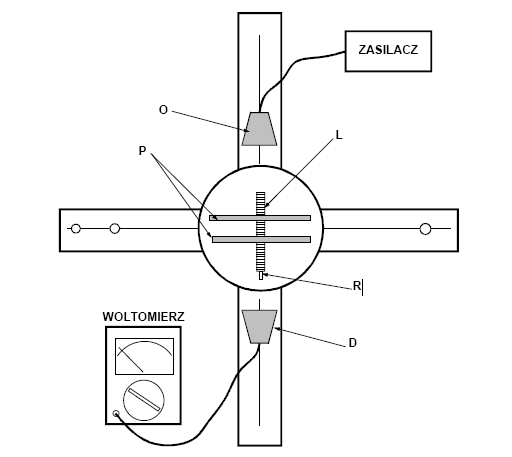
Rys.2. Schemat układu pomiarowego z interferometrem Fabry - Perota:

O - źródło fal elektromagnetycznych, P - płytki płaskorównoległe, D - detektor fal elektromagnetycznych, L - linijka, R - pokrętło do regulacji odległości między płytkami

Interferometr Fabry - Perota składa się z dwu płytek, takich, że przepuszczają one część promieniowania, ale mają dużą zdolność odbijającą. Płytki te ustawiamy w ten sposób, że powietrze pomiędzy płytkami tworzy dokładnie płasko równoległą warstwę, czyli płytki są do siebie równoległe. Fale, które przez górną płytkę przedostają się do warstwy powietrza, ulegają wielokrotnym odbiciom od ścianek płytek. Jeśli na pierwszą płytkę pada wiązka fal, to z drugiej płytki wychodzi szereg równoległych wiązek. Należy wiec tak regulować odległość między płytkami, aby obserwować wzmocnienia i osłabienia fal.

Siatką dyfrakcyjna to układ równoległych do siebie szczelin rozmieszczonych w równych odstępach. Niech a oznacza szerokość szczeliny, b szerokość odstępu między szczelinami. Odległość d środków sąsiednich szczelin nazywamy stalą siatki, a + b = d. Zgodnie z zasadą Huyghensa, każda szczelina staje się wtórnym źródłem fal, które rozchodzą się we wszystkich kierunkach. Wykonując ćwiczenie obracamy źródło fal dookoła siatki dyfrakcyjnej i mierzymy kąt obrotu, a ponieważ wzajemne wzmacnianie następuje, gdy:
możemy, więc obliczyć długość fali.

Długość fali elektromagnetycznej obliczamy ze wzoru:

Błąd pomiaru obliczamy używając metody różniczki logarytmicznej używając wzoru:

Obliczenia:

1. Pomiar długości fali na stanowisku C-12. Wyznaczenie długości fal dźwiękowych

l = 111 - (-1) = 112 mm

błąd odczytu Δd = 1 mm

n = 26 * 1

* = 2 ⋅ l / n = 2 ⋅ 112 / 26 = 8,62 mm

** = ( 2 / 26 ) ⋅ 1 + 2 ⋅ 112 ⋅ 1 / ( 26 ⋅ 26 ) = 0,41 mm

* = 8,62 mm * 0,41 mm

2. Pomiar długości fali na stanowisku C-9. Wyznaczenie długości mikrofali.

odczyt z linijki: l = 28,8 cm * 0.1

błąd odczytu Δd = 0,1 cm

n = 17 * 0

* = 2 ⋅ l / n = 2 ⋅ 28,8 / 17 = 3,39 cm

** = ( 2 / 17 ) ⋅ 0,1 + 2 ⋅ 28,8 ⋅ 1 / ( 17 ⋅ 17 ) = 0,21 cm

* = 3,39 cm * 0,012 cm

Są to zatem mikrofale, rzędu 10^-2

3. Wyznaczenie długości fali elektromagnetyczne zielonej. Pomiar długości fali na stanowisku C-10

Lp	x1 [mm]	x2 [mm]	lS [mm]	l [nm]	n	[nm]
1	11,85	11,69	0,16	16000	50	640
2	11,69	11,55	0,14	14000	50	560
3	11,55	11,39	0,16	16000	50	640
4	11,39	11,24	0,15	15000	50	600
5	11,24	11,10	0,14	14000	50	560
6	11,10	10,95	0,15	15000	50	600
7	10,95	10,80	0,15	15000	50	600
średnia			0,15	15000		600

Tabela 1. Wyniki pomiarów interferometrem Michelsona

l_S = 0.15 mm * 0.01

błąd odczytu Δd = 0,01 mm

m = 50 * 2

Współczynnik pokrętła = 0,1

Za wartość
przyjmiemy średnią arytmetyczną tych wartości. Otrzymujemy
. W dalszych rachunkach (jak się później okaże zarówno każda z obliczonych wartości
mieści się w granicach niepewności pomiarowej).

* = 2 ⋅ l / n = 2 ⋅ mm = 600 nm

** = ( 2 / 50 ) ⋅ 0,1 ⋅ 0,01 + 2 ⋅ 0,1 ⋅ 0,15 ⋅ 2 / ( 50 ⋅ 50 ) = 64 nm

* = 600 nm * 64 nm

4. Wyznaczenie długości fali elektromagnetycznej czerwonej. Pomiar długości fali na stanowisku C-11

Lp	x1 [mm]	x2 [mm]	lS [mm]	l [nm]	n	[nm]
1	9,10	9,27	0,17	17000	50	680
2	9,27	9,42	0,15	15000	50	600
3	9,42	9,57	0,15	15000	50	600
4	9,57	9,73	0,16	16000	50	640
5	9,73	9,88	0,15	15000	50	600
6	9,88	10,02	0,14	14000	50	560
7	10,02	10,18	0,16	16000	50	640
średnia			0,1543	15430		617

Tabela 1. Wyniki pomiarów interferometrem Michelsona

Ze względu na to, że nie interesują nas położenia zwierciadła przy pierwszym i 50-tym wzmocnieniu, a jedynie różnica tych odległości, zapisujemy w tabeli wielkość l, której odpowiada wartości l = x₂ - x₁. Ze względu na to, że śruba posiada 10-krotne przełożenie, a każde nasze przesunięcie powoduje dwukrotną zmianę (światło przebywa tę drogę dwukrotnie - przed odbiciem i po nim) wartość długości fali możemy wyznaczyć teraz korzystając ze wzoru

,

Za wartość
przyjmiemy średnią arytmetyczną tych wartości. Otrzymujemy
. W dalszych rachunkach (jak się później okaże zarówno każda z obliczonych wartości
mieści się w granicach niepewności pomiarowej).

Ze względu na to, że mogliśmy popełnić pomyłkę przy zliczaniu wzmocnień szacujemy

l_S = 0.1543 mm * 0.01

błąd odczytu Δd = 0,01 mm

m = 50 * 2

współczynnik pokrętła 0,1

* = 2 ⋅ l / n = 2 ⋅ mm = 617 nm

** = ( 2 / 50 ) ⋅ 0,1 ⋅ 0,01 + 2 ⋅ 0,1 ⋅ 0,1543 ⋅ 2 / ( 50 ⋅ 50 ) = 65 nm

* = 617 nm * 65 nm

Wnioski

Uzyskane wyniki mieszczą się w niepewnościach pomiarowych. Najdokładniej zmierzoną falą była mikrofala, ponieważ błąd obliczeń wyniósł 0,012 cm.

5

---