ROZDZIAŁ 1

1.1 Wyjaśnić pojęcia. Automatyzacja ,Automatyka, Teoria sterowania, Sterowanie ręczne, Sterowanie automatyczne

1.2 Scharakteryzować historię rozwoju automatyki.

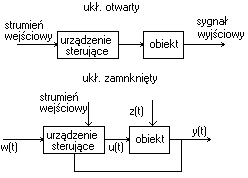
1.3 Wyjaśnić istotę sterowania w układzie zamkniętym i otwartym. Przykłady.

1.4 Czym różni się sterowanie od regulacji?

1.5 Wady i zalety sterowania w układzie otwartym i zamkniętym.

1.6 Wyjaśnić pojęcia:Sygnał wejściowy, Sygnał wyjściowy, Sygnał uchybu, Regulator, Człon wykonawczy, Obiekt sterowania, Sprzężenie zwrotne, Przetwornik pomiarowy,

1.7 Wymienić podstawowe zadania układów automatycznej kontroli, sygnalizacji, zabezpieczeń i blokad. Przykłady.

1.8 Dokonać podstawowej klasyfikacji układów automatyki. Krótko omówić poszczególne układy.

1.9 Podać przykłady:układy stabilizacji, układy śledzące, układy optymalne

ROZDZIAŁ 2

2.1 Korzyści przekształcenia Laplace`a.

2.2 Właściwości przekształcenia Laplace`a.

2.4 Układ dyskretny to:

2.5 Dyskretyzacja sygnału jest to:

2.6 Kwantyzacja i próbkowanie sygnału:

2.8 Funkcja ekstrapolatora w układzie:

2.9 Przykładowe widmo sygnału ciągłego i dyskretnego dla s. harmonicznego:

2.10 Twierdzenie Kotielnikowa - Shannona:

2.11 Istota przekształcenia Z:

2.12 Podstawowe właściwości przekształcenia Z:

2.13 Metody odwrotnego przekształcenia Z:

ROZDZIAŁ 3

3.1 Podstawowe formy opisu układu dyskretnego:

3.2 Opis układu za pomocą równania różniczkowego:

3.3 Opis układu za pomocą równania różnicowych:

3.4 Opis układu za pomocą transmitancji operatorowej:

3.5 Opis układu za pomocą transmitancji widmowej układu ciągłego i dyskretnego:

3.6 Wyznaczanie char. statycznej układu w oparciu o transmitancję operatorową, eksperymentu i równania operatorowego. Co to jest charakterystyka statyczna ukł.:

3.7 Opis układu ciągłego za pomocą równań stanu:

3.8 Opis układu dyskretnego za pomocą równań stanu:

3.10 Omówić podstawowe charakterystyki czasowe układu ciągłego i dyskretnego:

3.11 Analityczne i eksperymentalne wyznaczenie char. częstotliwościowych:

ROZDZIAŁ 4

4.1 Standardowe sygnały wymuszające:

4.2 Scharakteryzować klasyczne metody analizy.

4.3 Omów operatorowe metody analizy

4.4 Jakie są podstawowe zasady budowy schematów blokowych.

4.5 Podstawowe metody przekształcania schematów blokowych.

4.6 Wyprowadzić zależności określające transmitancje ciągłego i dyskretnego układu:otwartego, zamkniętego oraz uchybową

4.7 Wymienić i omówić metody dyskretnej aproksymacji układów ciągłych:

4.8 Wymienić i podać interpretację fizyczną podstawowych parametrów członów dynamicznych i układów regulacji

4.9 Jakie są sposoby wyznaczania uchybu ustalonego?

4.10 Jakie są podstawowe człony dynamiczne i ich transmitancje?

4.11 Zapisać transmitancje układu ciągłego bez zer i z zerami w przestrzeni stanów

4.12 Zapisać transmitancje układu dysktertnego bez zer i z zerami w przestrzeni stanów

4.13 Co to są wartości własne układu.

4.14 Przedstawić odpowiedź układu swobodnego i wymuszonego, opisanego równaniami stanu.

ROZDZIAŁ 5

5.1 Wyjaśnić pojęcia:układ stabilny, układ stabilny asymptotycznie, układ stabilny nieasymptotycznie, układ niestabilny. układ stabilny globalnie

5.2 Co to jest punkt(stan) równowagi?

5.3 Podać warunek konieczny i wystarczający stabilności asymptotycznej układu.

5.4 Algebraiczne kryteria stabilności : Kryterium Routha, kryterium Hurwitza, kryterium częstotliwościowe

5.5 Częstotliwościowe kryteria stabilności

Rozdział 1

1. Wyjaśnić pojęcia.

Automatyzacja - rozwój maszyn i urządzeń pozwalających zastępować człowieka w jego pracy umysłowej, wzrost produkcji, wydajności, jakości i oszczędności.

Automatyka - nauka zajmująca się teorią i praktyczną realizacją nadzoru i sterowania obiektami technologicznymi bez udziału lub z udziałem człowieka.

Teoria sterowania - nauka o zjawiskach zachodzących podczas pracy np. jakiegoś urządzenia(teoria automatyki).

Sterowanie ręczne - na strumień wejściowy wpływa człowiek.

Sterowanie automatyczne - na strumień wejściowy wpływa urządzenie sterujące.

2. Scharakteryzować historię rozwoju automatyki.

1. okres sztuki -XVIII i XIX w. - wynalezienie maszyny parowej, silnika spalinowego i elektrycznego, regulatory;

2. okres przejściowy -1900-40 -linie telefoniczne, taśma montażowa, rozwój przemysłu przetwórczego i chemicznego. Narodziny lotnictwa.

3. okres nauki - maszyna cyfrowa, rozwój przemyslu zbrojeniowego, tranzystor, rozwój automatyki, maszyn matematycznych.

1. Wyjaśnić istotę sterowania w układzie zamkniętym i otwartym. Przykłady.

Układ otwarty - połączenie pewnej liczby członów szeregowo. Wielkością sterującą zmienianą w sposób świadomy, oddziaływuje się na obiekt sterowania, aby wielkość wyjściowa przyjmowała żądaną w czasie wartość. Wielkość wyjściowa nie wpływa na wielkość wejściową.

Układ zamknięty - urządzenie sterujące gwarantuje wartość sygnału sterującego u(t) na podstawie wartości sygnałów w(t) i y(t).

e(t) = w(t) - y(t)

2. Czym różni się sterowanie od regulacji?

Sterowanie - wywołanie celowych zmian wartości sygnałów wejściowych obiektu.

Regulacja - e(t) = w(t) - y(t) musi być zawsze możliwie bliska zera. Wartość u(t) musi być tak dobierana, aby to było spełnione(są to zmiany np. wskutek zakłóceń - niecelowe).

3. Wady i zalety sterowania w układzie otwartym i zamkniętym.

W układzie otwartym wielkość sterująca powinna być dostosowana nie tylko do pożądanej wartości wyjściowej, ale także do zakłóceń. Wielkość wyjściowa często(zakłócenia) odchyla się znacznie od żądanej wartości.

4. Wyjaśnić pojęcia:

Sygnał wejściowy - strumienie wprowadzone na wejście i wpływające na procesy zachodzące w obiekcie.

Sygnał wyjściowy - strumienie wyjściowe lub niektóre wielkości z nimi związane.

Sygnał uchybu - różnica sygnałów wejścia i wyjścia e(t) = w(t) - y(t) . Wprowadzany do regulatora.

Regulator - urządzenie wytwarzające odpowiedni sygnał sterujący u(t), tak aby wartość błędu była możliwie bliska zeru.

Człon wykonawczy - przetwarza sygnał o naturze przystosowanej do sterowania obiektem.

Obiekt sterowania - urządzenie, w którym zachodzą procesy technologiczne.

Sprzężenie zwrotne - powoduje, że wartość danego sygnału zależy też od sygnału innego, np. y(t).

Przetwornik pomiarowy - układ przetwarzający dany proces na proces o takim samym kształcie, ale o innej na ogół strukturze fizycznej.

5. Wymienić podstawowe zadania układów automatycznej kontroli, sygnalizacji, zabezpieczeń i blokad.

Przykłady.

Kontrola - wykrywa czy obiekt jest dobry czy uszkodzony
( na podstawie pomiarów).

Sygnalizacja - prowadzona za pomocą różnych wskaźników optycznych i akustycznych lub niekiedy też za pomocą drukarek, itp. Zadaniem jej jest przekazanie informacji o obiekcie operatorowi.

Diagnostyka - lokalizacja uszkodzenia.

Zabezpieczenia i blokady - w wypadku awarii należy natychmiast podjąć działania, aby ją zlikwidować lub nie dopuścić do dalszych awarii obiektów. Następuje automatyczne wyłączenie obiektu z sieci, itp. Niekiedy wyłączanie następuje z opóźnieniem bądź też wymagane jest przełączenie na inne nie uszkodzone urządzenia, itp.

Np. statek, duże sieci rurociągowe.

6. Dokonać podstawowej klasyfikacji układów automatyki. Krótko omówić poszczególne układy.

1. ze względu na zadanie układu:

• układy stabilizacji - utrzymanie stałej wartości wielkości wyjściowej;

• układy śledzące - powodują nadążanie wielkości wyj. za zmianami wielkości wej.

• układy programowe - sygnał wej. Jest z góry określoną funkcją czasu(zmienia się według danego programu);

• układy optymalne - układy, których struktura i parametry regulatora są określane na podstawie ekstremalizacji przyjętego wskaźnika jakości.

Otwarte układy optymalne - w oparciu o ekstremalizację wskaźnika jakości określa się syg. wej. W funkcji czasu.

Zamknięte układy optymalne - sprzężenie zwrotne. Strukturę i parametry regulatora określa się z warunku ekstremalizacji wskaźnika jakości.

Statyczne układy otwarte - ekstremalizacja wskaźnika jakości, który jest funkcją wielu zmiennych.

Dynamiczne układy otwarte - ekstremalizacja wskaźnika jakości, który jest funkcjonałem.

• układy przełączające - zapewniają realizację składowych operacji procesu

technologicznego w określonej kolejności. Rolę regulatora spełnia układ logiczny.

2. ze względu na liniowość elementów:

• układy liniowe - spełniają zasadę superpozycji;

• układy nieliniowe - nie spełniają zasady superpozycji i nie mogą być opisane za pomocą równań liniowych;

3. ze względu na charakter sygnałów:

• układy ciągłe - syg. są funkcjami ciągłymi;

• układy dyskretne - przynajmniej jeden syg. ma charakter dyskretny. Równania różnicowe.

4. ze względu na występowanie procesu przejściowego:

• statyczne - wyj. zależy tylko od wej. w dowolnej chwili;

• dynamiczne - zależy dodatkowo od procesu przejściowego i stanu układu w chwili początkowej.

5. ze względu na liczbę wyjść i wejść:

• jednowymiarowe - jedno wej. i wyj.

• wielowymiarowe - wiele wej. i wyj.

6. ze względu na charakter zmienności wymuszeń i parametrow:

• deterministyczne - wymuszenia lub parametry są stałymi lub zdeterminowanymi funkcjami czasu;

• stochastyczne - wymuszenia lub parametry są funkcjami lub wielkościami przypadkowymi;

7. ze względu na zdolności do samoczynnego nastrajania parametrów do zmieniających

się ch-k obiektu lub zakłóceń:

• układ zwykły - nie mają zdolności;

• układy adaptacyjne - mają;

8. ze względu na zmienną strukturę:

- układy o stałej strukturze;

- układy o zmiennej strukturze;

1. Podać przykłady:

układy stabilizacji - układ regulacji poziomu cieczy w zbiorniku;

układy śledzące - układ sterowania ogniem artylerii przeciwlotniczej według

wskazań radaru.

układy optymalne - sterowanie w czasie ciągiem silników, aby samolot zużył mało

paliwa i osiągnął pułap.

Rozdział 2

2.1 Korzyści przekształcenia Laplace`a.
-- włącza automatycznie warunki

początkowe,

-- rozwiązanie uzyskuje się przez proste operacje algebraiczne

-- praca jest usystematyzowana,

-- umożliwia proste ujecie nieciągłych sygnałów wejściowych,

-- rozwiązanie ogólne i szczególne uzyskuje się jednocześnie.

2.2 Właściwości przekształcenia Laplace`a.
-- liniowość

-- przesunięcie w dziedzinie zmiennej

rzeczywistej

-- przesunięcie w dziedzinie zmiennej zespolonej

-- różniczkowanie w dziedzinie zmiennej

rzeczywistej

-- transformata funkcji okresowej

2.4 Układ dyskretny to:

Taki układ z próbkowaniem sygnału. Układy dyskretne są układami regulacji automatycznej, w których informacja jest przekazywana tylko w dyskretnych chwilach, zwanych chwilami
impulsowania. U. De. Mogą być liniowe i nieliniowe.

Schemat blokowy D. Uu. regulacji
2.5 Dyskretyzacja sygnału jest to:

Przekształcenie sygnału ciągłego w dyskretny. Rozróżnia się dyskretyzację w poziomie [kwantowanie] i w czasie [próbkowanie].

2.6 Kwantyzacja i próbkowanie sygnału:

Kwantowanie sygnału występuje np. w układach przekaźnikowych

f(t) s. kwantowy f(t) s. próbkowy

t t

• 0 T 2T 3T 4T 5T 6T
  

2.8 Funkcja ekstrapolatora w układzie:
W układzie praktycznym funkcję tą spełnia przetwornik A/C.
Jego zadaniem jest aproksymacja sygnału między kolejnymi
próbkami, zwykle funkcją stałą

9. Przykładowe widmo sygnału ciągłego i dyskretnego dla
s. harmonicznego:
/F(j)/

A

widmo s. ciągłego



_o

/F^*(j)/ prążek podstawowy

A/T

+

_o- 3_i _o- 2_i _o  + _i  + 2_i

_o- 3_i

2.10 Twierdzenie Kotielnikowa - Shannona:

Określa ono związek pomiędzy sygnałem ciągłym a sygnałem
próbkowanym. Sygnał ciągły, próbkowany z częstotliwością co
najmniej dwukrotnie większą od granicznej częstotliwości swego
widma, może być ponownie odtworzony z sygnału impulsowego.
2.11 Istota przekształcenia Z:

Przekształceniem (transformatą) Z dyskretnej funkcji czasu f^*(t)
jest nazywane przekształcenie operatorowe określone wzorem:
F(z) =

Transformaty Z istnieją dla funkcji dyskretnych, które rosną
szybciej od funkcji wykładniczych.Na przykład dla funkcji
dyskretnych f(k) = k! oraz f(k)=exp(ak²) (a
0) nie istnieją
transformaty Z, ponieważ funkcje te rosną szybciej od funkcji
wykładniczych.
2.12 Podstawowe właściwości przekształcenia Z:

- Twierdzenie o liniowości
- Twierdzenie o przesunięciu w dziedzinie czasu
- Twierdzenie o transformacie różnicy
- Twierdzenie o wartości końcowej

2.13 Metody odwrotnego przekształcenia Z:
Odwrotne przekształcenie Z można zrealizować 3 metodami:
rozkładu na ułamki proste,
szeregu potęgowego,
odwrotnego przekształcenia Z (residuów).
Metoda rozkładu na ułamki proste:

Oryginał transformaty wyraża się zależnością
f(kT)=

z tego równania otrzymuje się:
f(kT)=

Przykład:
Wyznaczyć oryginał transformaty:

Oryginał transformaty wyznacza się korzystając z wzoru 1.

ROZDZIAŁ 3

3.1 Podstawowe formy opisu układu dyskretnego:

Równania różniczkowe, równania stanów, transmitancje

operatorowe lub widmowe, charakterystyki czasowe lub

częstotliwościowe.

3.2 Opis układu za pomocą równania różniczkowego:

Równanie różniczkowe zwyczajne, opisujące ciągły,

jednomiarowy obiekt sterowania o stałych skupionych ma ogólną

postać:

F = (y, y`, ..., y<sup>n</sup>, u, u`, ..., u^m, z, z`, ..., z^k, t) = 0

gdzie: y- sygnały wyjściowy, u - sygnał wejściowy ,
z - zakłócenia działające na obiekt

Równanie to opisuje obiekt jednowymiarowy nieliniowy

i niestacjonarny. Gdy obiekt jest stacjonarny nie występuje

bezpośrednia zależność od czasu, co oznacza że parametry

układu są stałe. Gdy obiekt jest liniowy to w/w równanie liniową

kombinacją sygnałów i ich pochodnych. W przypadku ciągłego i

stacjonarnego układu liniowego równanie można zapisać:

Zależnie od warunków pracy rozróżnia się cztery przypadki:

--- na obiekt działa zarówno sygnał sterujący u(t) jak i sygnał

zakłócający z(t). Dynamikę obiektu opisuje równanie (2),

--- na obiekt działa tylko sygnał sterujący, a zakłócenie i jego

pochodna są równe 0,

--- na obiekt nie działa sygnał sterujący, natomiast działa

zakłócenie z(t)

--- na obiekt nie działają żadne zakłócenia zewnętrzne i wzór (2)

upraszcza się do postaci:

3.3 Opis układu za pomocą równania różnicowych:

W układach dyskretnych jest równanie różnicowe, w którym
czas ma wartość dyskretną. Równanie różnicowe można
otrzymać z równania różniczkowego, zastępując pochodną
różnicy I- go rzędu. Rozróżnia się różnice: wyprzedzone,
wsteczne i centralne.

Pochodne sygnału f(t) w chwili t = kT (k= 0, 1, 2) może być

wyznaczona z zależności (różnica wyprzedzona):

gdzie: f(k) = f(kT), f(k+1)=f[(k+1)T].

3.4 Opis układu za pomocą transmitancji operatorowej:

Układu ciągłego i dyskretnego: Transmitancję operatorową G(s) jednowymiarowego układu liniowego i stacjonarnego nazywa się wielkość określoną jako stosunek transformaty Laplace`a Y(s) sygnału wejściowego obiektu do transformaty U(s) sygnału wejściowego, przy zerowych warunkach początkowych.

przy czym transformaty Y(s) i U(s) określone są następująco:

nie G(s) tylko U(s)

Transmitancją dyskretną G(z) jednowymiarowego układu dyskretnego jest nazwana wielkość określona jako stosunek dyskretnej transformaty Laplace`a sygnału wejściowego Y(z) dla transformaty sygnału wejściowego U(z) przy założeniu że warunki początkowe są zerowe.

dla układu liniowego opisanego liniowymi równaniami, transmitancja jest wielowymiarową funkcją wymierną zmiennej Z o postaci:

3.5 Opis układu za pomocą transmitancji widmowej układu ciągłego i dyskretnego:

Jeżeli na wejście elementu liniowego wprowadzone zostanie

wymuszenie harmoniczne o stałej pulsacji , to na wyjściu

po zaniknięciu przebiegu przejściowego ustali się odpowiedź

harmoniczna o tej samej pulsacji, ale w ogólnym przypadku o

innej amplitudzie i fazie niż wymuszenie. Teoretyczną

podstawę analizy w dziedzinie częstotliwościowej stanowi

transmitancja widmowa.

1. jako iloraz dwóch wielkości zespolonych

przy czym:

a()= b₀ - b₂² + b₄⁴ - b₆⁶ + ...

b()= b₁ - b₃³ + b₅⁵ - b₇⁷ + ...

c()=a₀ -a₂² + a₄⁴ - a₆⁶ + ...

d()=a₁ - a₃³ + a₅⁵ - a₇⁷ + ...

2. jako suma składnika rzeczywistego i urojonego

(postać algebraiczna) po uwzględnieniu wzoru z a)

3. w postaci wykładniczej

4. w postaci trygonometrycznej

G(j) = /G(j)\[cos () + jsin()]

Układ dyskretny liniowy o wymuszeniu harmonicznym

U(t) = U₀sint, złożony z idealnego impulsatora, ekstrapolatora i członu dynamicznego reprezentującego obiekt sterowania.

3.6 Wyznaczanie char. statycznej układu w oparciu o

transmitancję operatorową, eksperymentu i równania

operatorowego. Co to jest charakterystyka statyczna ukł.:

Charakterystyka statyczna układu jest to zależność sygnału wyjściowego od wejściowego w stanie ustalonym.

Sposoby wyznaczania:

1. z równania różniczkowego ---> przez przyrównanie wszystkich

pochodnych do 0

2. eksperymentalnie ---> wprowadzając na wejście stały sygnał i

mierząc w stanie ustalonym jago wartość na wyjściu,

dokonując kilku pomiarów dla różnych ale stałych

wartości sygnału wejściowego, otrzymuje się zbiór

punktów, który po odpowiedniej aproksymacji pozwoli

nakreślić charakterystykę statyczną.

3.7 Opis układu ciągłego za pomocą równań stanu:

Schemat blokowy układu dynamicznego opisanego równaniem różniczkowym

Dynamikę tego układu można zapisać w postaci równań stanu. W ujęciu matematycznym polega to na zastąpieniu równania różniczkowego II - go rzędu układem równań różniczkowych

I - go rzędu. W tym celu zostaną przyjęte dwie pomocnicze zmienne x₁ i x₂, zdefiniowane następująco:

x₁(t) = y(t) x₂(t) = y`(t)

Po zróżniczkowaniu stronami:

x`<sub>1</sub>(t) = y`(t) = x₂(t)

x`<sub>2</sub>(t) = y``(t) = ­ a<sub>0</sub>y(t) - a<sub>1</sub>y`(t) + u(t)

ostatecznie, uwzględniając równania:

x`₁(t) = x₂(t)

x`₂(t) = - a₀x₁(t) - a₁x₂(t) + u(t)

Równania w postaci wektorowo - macierzowej:

3.8 Opis układu dyskretnego za pomocą równań stanu:

x(k+1) = Ax(k) + Bu(k) gdzie: B = A_C^-1 [exp (A_CT) - I]B_C

y(k) = Cx(k) + Du(k) C = C_C, D = D_c

Po pominięciu nieliniowych członów rozwinięcia z szeregu

potęgowego macierzy exp (A_CT) co prowadzi do zależności

przybliżonych:

A  I + A_CT

B  B_CT

3.10 Omówić podstawowe charakterystyki czasowe układu

ciągłego i dyskretnego:

DLA CIĄGŁĘGO:

Najbardziej rozpowszechnionymi charakterystykami czasowymi

są charakterystyki (odpowiedzi) skokowe h(t) i impulsowe g(t).

Char. jednostkową (skokową) jednowymiarowego układu

liniowego nazywa się odpowiedź tego układu na sygnał

jednostkowy 1(t), przy zerowych warunkach początkowych.

Char. skokowa dobrze charakteryzuje zarówno właściwości

statyczne jak i dynamiczne układu. Wyznaczając ją dla różnych wartości amplitud sygnału wejściowego łatwo można dokonać weryfikacji liniowości układu, gdyż w przypadku układów liniowych charakter procesu przejściowego odpowiedzi skokowej jest niezależny od amplitudy sygnału wejściowego.

Sygnały skokowe często występują w układach elektrycznych,

mechanicznych, hydraulicznych itd.

Charakterystyką (odpowiedzią) impulsową nazywa się

odpowiedź układu na sygnał wejściowy w postaci impulsu

Diraca, przy zerowych warunkach początkowych.

DLA DYSKRETNEGO:

Dyskretnymi charakterystykami (odpowiedziami) czasowymi są nazywane odpowiedzi w stanie nieustalonym dyskretnych

układów liniowych na odpowiednie wymuszenia, przy zerowych

warunkach początkowych. Podstawowymi dyskretnymi

char - mi. czasowymi są: dyskretna char impulsowa idyskretna

char. skokowa.

Dyskretną charakterystyką (odpowiedzią) impulsową

g(k)= g(kT) dyskretnego układu liniowego nazywa się dyskretną odpowiedź tego układu na wymuszenie w postaci funkcji Diraca δ(k) przy zerowych warunkach początkowych. Między impulsową g(k),a ciągłą char. impulsową g(t) zachodzi zależność:

g(k) = g(t)/ G(s) = k/sT₁+1

/t=kT

Dyskretną charakterystyką (odpowiedzią) skokową H(k)

dyskretnego układu liniowego nazywa się dyskretną odpowiedź

tego układu na wymuszenie w postaci jednostkowej funkcji

skokowej przy zerowych warunkach początkowych i w tym

przypadku jest słuszna zależność: h(k) = h(t)/

/t=kT

3.11 Analityczne i eksperymentalne wyznaczenie char.

częstotliwościowych:

eksperymentalnie ---> wyznaczenie charakterystyki polega na

zarejestrowaniu w stanie ustalonym przebiegu wyjściowego

obiektu, gdy do wejścia jest doprowadzony sinusoidalny sygnał

pobudzający o stałej amplitudzie i częstotliwości. Dokonanie

tego typu pomiarów dla różnych częstotliwości sygnału pozwala

znaleźć kolejny punkt charakterystyki częstotliwościowej, a tym

samym charakterystyka w pełni charakteryzuje właściwości

obiektu. Zalety analizy częstotliwościowej:
a) kolejne punkty charakterystyki wyznacza się oddzielnie, za

każdym razem używając pełnej dopuszczalnej amplitudy sygnału

we., wpływ zakłóceń jest mniejszy niż przy metodach czasowych

b) jeżeli w przebiegu wy. Wydzieli się np. przez zastosowanie

filtru tylko składową przebiegu o aktualnie mierzonej

częstotliwości, wpływ zakłóceń zostanie poważnie zmniejszony.

Do dokonania pomiarów, w celu wyznaczenia charakterystyk

częstotliwościowych, jest niezbędne zastosowanie generatora

przebiegów sinusoidalnych. Potrzebny w praktyce zakres

pomiarowy waha się w granicach od ok. 0,01 do kilkudziesięciu

herców. Na wejście badanego układu jest podawane wymuszenie

harmoniczne o postaci: u(t) = U_Osint

Jeżeli na obiekt liniowy nie działają żadne dodatkowe siły

sterujące i zakłócenia, wówczas na wejście układu w stanie

ustalonym pojawia się sygnał wyjściowy y(t) opisany

zależnością:

y(t) = Y_Osin(t + )

Odpowiedź obiektu na wymuszenie harmoniczne:

u(t) = U_Osint

ROZDZIAŁ.4

1. Standardowe sygnały wymuszające:

• Skok jednostkowy 1(t). Czas jego narastania jest = 0, co jest tylko przybliżeniem sygnału rzeczywistego. Stosuje się też sygnał skokowy o amplitudzie Uo , który zapisuje się w postaci

u(t) = Uo1(t)

• Impuls (funkcja) Diraca δ (t). Impuls Diraca jest definiowany jako impuls o nieskończenie wielkiej amplitudzie i nieskończenie małym czasie trwania oraz o polu równym jedności.. Funkcja ta przedstawia np.: impuls elektryczny

• Funkcje potęgowe. Ogólnie można przedstawić w postaci: u(t) = Uotⁿ*1(t) gdzie: n = 1,2,.... Jeśli n = 1 ,to u(t) jest funkcją liniowo- narastającą, jeżeli n = 2 - funkcja paraboliczna

• Funkcja harmoniczna. Najczęściej stosuje się sygnał sinusoidalny o postaci u(t) = Uo sint.

1. Scharakteryzować klasyczne metody analizy.

Klasyczne metody analizy bazują na teorii rozwiązania równań różniczkowych. Mogą być stosowane wyłącznie w przypadku liniowych równań różniczkowych zwyczajnych. Mają one jednak tę zaletę, że w wyniku uzyskuje się rozwiązanie w ogólnej analitycznej postaci, słuszne dla wszystkich dopuszczalnych wartości parametrów i warunków początkowych. Rozwiązanie jest sumą dwóch części: rozwiązania szczególnego oraz z rozwiązania ogólnego.

Są dwie klasyczne analizy:

Rozwiązania szczególnego równania niejednorodnego, które opisuje zachowanie się układu w stanie ustalonym; rozwiązanie to często jest nazywane składową wymuszoną i charakteryzuje właściwości modelu matematycznego w odniesieniu do danego wymuszenia,

Rozwiązania ogólnego równania jednorodnego, opisującego stan nieustalony układu; rozwiązanie to jest nazywane także składową swobodną.

4.3 Omów operatorowe metody analizy

Klasyczna metoda rozwiązywania równań różniczkowych staje się pracochłonna gdy użyty jest sygnał wejściowy w postaci funkcji nieciągłej lub rzędu równania większego niż drugi. Wyznaczanie jest żmudne. W wymienionych przypadkach stosowane są metody numeryczne ( np. metoda Runge-Kuty czwartego rzędu) lub sporadycznie metody operatorowe.

Metody operatorowe:

1. schematy blokowe

2. postać kanoniczna układu ze sprzężeniem zwrotnym

3. dyskretna aproksymacja układów ciągłych

4. podstawowe parametry członów dynamicznych i układów regulacji

5. regulacja statyczna i dynamiczna

1. Jakie są podstawowe zasady budowy schematów blokowych.

Schematy blokowe stosuje się do graficznego przedstawienia zależności występujących w układach automatyki. Schematy te przedstawiają wzajemne powiązania pomiędzy poszczególnymi zespołami analizowanego elementu lub układu, tzn. podają kierunki przepływu sygnałów oraz związki między sygnałami wejściowymi i wyjściowymi wszystkich zespołów . Znajomość schematu blokowego niekiedy ułatwia wyznaczenie opisu matematycznego układu i analizę jego właściwości.

W celu doprowadzenia ich do postaci dogodnej pod względem przeprowadzonych rozważań. Jest to możliwe ze względu na jednorodność i addytywność układów liniowych.

2. Podstawowe metody przekształcania schematów blokowych.

• Metoda przekształceń układu równań opisujących stosuje się najczęściej na etapie budowy schematu blokowego.

• Metoda krok po kroku pozwala zarówno przekształcać, jak i upraszczać schemat blokowy, stosuje się ją do przekształcania dowolnie skomplikowanych schematów.

• Metoda mnemotechniczna stosuje się do przekształcania schematów blokowych ograniczonej klasy układów, tj. schematów, które w torze głównym nie mają połączeń równoległych, lecz znaną liczbę połączeń szeregowych i sprzężeń zwrotnych

• Metoda Masona

4.6 Wyprowadzić zależności określające transmitancje ciągłego i dyskretnego układu: otwartego, zamkniętego oraz uchybową

Transmitancja ciągła:

Transmitancja układu otwartego:

Transmitancja układu zamkniętego:

Transmitancja uchybowa

Transmitancja dyskretna:

Transmitancja układu otwartego:

Transmitancja układu zamkniętego:

Transmitancja uchybowa

1. Wymienić i omówić metody dyskretnej aproksymacji układów ciągłych:

1. Metoda 1 (w oparciu o tablice transformat)

Kolejność postępowania:

- wyznaczyć char. impulsową g(t)

g(t) = ^-1[G(s)]

- wyznaczyć dyskretną char. impulsową:

g(kT) = g(t) _t=kT

- dla wyznaczonej charakt. G(t) lub g(kT) odczytać

transmitancję G(z)

2. Metoda 2 (bazująca na wyznaczeniu char. impulsowej)

Dyskretną charakterystykę impulsową g(kT), dla danej transmitancji G(s), wyznacza się zgodnie z zależnością:

g(kT) = g(t) _t=kT

Transmitancję dyskretną określona jest zależnością:

G(z) = Z [g(kT)]

3. Metoda3 (dyskretna aproksymacja pochodnych)

Metoda ta bazuje na aproksymacji pochodnej za pomocą różnicy pierwszego rzędu:

4. Metoda 4 (metoda operatorów całkowych)

Metoda operatorów całkowych Tustina i metoda form z. Ogranicza się ona do wykorzystania, wprowadzonej przez Tutsina definicji operatorów całkowania. Operatorem całkowania Tutsina ma postać:

7. Wymienić i podać interpretację fizyczną podstawowych parametrów członów dynamicznych i układów regulacji.

1. Współczynnik wzmocnienia statycznego K, który określa wzmocnienie układu w stanie ustalonym przy stałym sygnale wejściowym. Gdy k=0,
, gdy k>0 oblicza się wzmocnienie prędkościowe, przyspieszeniowe, itd.

2. Wzmocnienie amplitudowe określone jako
. Między K a wzmocnieniem zachodzi

3. Stała czasowa

Układ wyższego rzędu posiada wiele stałych czasowych, których wartości są odwrotnością wartości biegunów transmitancji G(s).

Układ 2-go rzędu charakteryzują parametry:

1. Współczynnik tłumienia .

2. Pulsacja drgań własnych nietłumionych _n, pulsacja drgań odpowiedzi układu w przypadku braku tłumienia, tj. dla =0.
=2f

3. pulsacja drgań własnych tłumionych _t. Jest to pulsacja dla >0

4. Okres drgań

5. Przeregulowanie

6 Wskaźnik tłumienia (oscylacyjności) d

7. Czas narastania

8. Czas ustalania (czas regulacji) t_r. Jest to czas kiedy osiągnie przez odpowiedź skokową układu stan ustalony z określoną dokładnością , którą podaje się w procentach.

9. Uchyb ustalony e_u. parametr ten określa wartość uchybu e(t) w stanie ustalonym. Charakteryzuje tylko układ regulacji.

8. Jakie są sposoby wyznaczania uchybu ustalonego?

gdzie

trzy pierwsze uchyby mają swoje nazwy

- położeniowy
- prędkościowy
- przyspieszeniowy

9. Jakie są podstawowe człony dynamiczne i ich transmitancje?

1. proporcjonalny

y(t)=ku(t), G(s)=k

2. inercyjny I - go rzędu

3. całkujące

,
gdzie T_i - czas zdwojenia

4. różniczkujący

, G(s)=ks

5. II - go rzędu

6. opóźniający

gdzie T₀ - czas opóźnienia

7. przesównik fazowy

8. forsujący G(s)=1+Ts

10. Zapisać transmitancje układu ciągłego bez zer i z zerami w przestrzeni stanów

Transmitancja bez zer:

Transmitancja z zerami:

1.Przypadek gdy m.<n

2.Przypadek gdy m.=n

1. Co to są wartości własne układu.

Równanie charakterystyczne macierzy stany A określone jest w postaci wyznacznika

det(I-A)=0 a jego pierwiastki ₁,₂,...,_N nazwane są wartościami własnymi.

2. Przedstawić odpowiedź układu swobodnego i wymuszonego, opisanego równaniami stanu.

- składowa swobodna
- składowa wymuszona

ROZDZIAŁ 5

5.1 Wyjaśnić pojęcia:

układ stabilny - wielkość wyj., jako odpowiedź na dowolne ograniczone wymuszenie, jest ograniczona. Musi być spełniona równość lim y(t) = yu(t) lub lim yn(t) = 0. Składowa nieustalona wielkości wyj. y(t) zanika z biegiem czasu i układ, po ustaniu działania wymuszenia, wraca do stanu przed zmianą wymuszenia.

Jeśli y_n(t) dla t→ po zaniknięciu wymuszenia zdąża do stanu równowagi to układ jest stabilny asymptotycznie. Gdy odpowiedź y_n(t) dla t→ nie zdąża do stanu równowagi, ale jest ograniczona, to układ jest stabilny nieasymptotycznie.

Natomiast gdy y_n(t) → dla t→, to układ jest niestabilny.

Stabilny globalnie - stabilność dla dowolnych warunków początkowych(stan nieustalony zanika dla dowolnych warunków początkowych). Stabilny lokalnie - stan nieustalony zanika tylko dla niektórych warunków początkowych.

5.2 Co to jest punkt(stan) równowagi?

Punkt(stan) równowagi - stan do jakiego wraca stabilny układ, po ustaniu działania wymuszenia(do takiego, w jakim znajdował się przed zmianą wymuszenia).

5.3 Podać warunek konieczny i wystarczający stabilności asymptotycznej układu.

Warunek konieczny i dostateczny stabilności asymptotycznej:

- wszystkie pierwiastki równania charakterystycznego, wszystkie części rzeczywiste pierwiastków zespolonych muszą być ujemne, czyli leżeć w lewej półpłaszczyźnie zmiennej zespolonej.

Układ jest stabilny nieasymptotycznie (stabilny w sensie Lapunowa), gdy oprócz pierwiastków leżących w lewej półpłaszczyźnie ma:

- jeden pierwiastek równy zero;

- pojedyncze pary pierwiastków urojonych;

- jeden pierwiastek rzeczywisty i pojedyncze pary pierwiastków urojonych.

5.4 Algebraiczne kryteria stabilności

Warunek konieczny: wszystkie współczynniki równania

a_nsⁿ+a_n-1s^n-1+...+a₁s+a₀=0 były jednego znaku i niezerowe.

Warunki dostateczne: kryterium Routha i Hurwitza.

Pozwalają one stwierdzić, czy liniowy układ jednowymiarowy jest stabilny asymptotycznie, na podstawie wartości współczynników równania charakterystycznego - bez jego rozwiązania.

1. Kryterium Routha.

Aby stwierdzić stabilność układu, który spełnia podany warunek konieczny, wyznacza się tzw. tabelę Routha i na podstawie właściwości jej wyrazów sprawdza się czy jest spełniony warunek dostateczny stabilności asymptotycznej.

gdzie b_i oraz niższe elementy oblicza się ze wzorów:
,
,
itd.

2. Kryterium Hurwitza.

Musi być spełnione kryterium algebraiczne (wszystkie pierwiastki muszą leżeć w lewej półpłaszczyźnie), oraz podwyznaczniki muszą być niezerowe (stabilny), zerowe (stabilny nieasymptotycznie) mniejsze od zera (niestabilny)

4. kryterium częstotliwościowe (można badać układ zamknięty przy pomocy charakterystyk ukł. otwartego).

Warunki dostateczne zostały podane przez Hurwitza. Kryterium H. Podaje warunki ,które powinny być spełnione aby równani char. układu miało wyłącznie pierwiastki leżące w lewej półpłaszczyźnie zmiennej zespolonej s.

Aby to zachodziło , muszą być spełnione warunki:

ai > 0, i=0,1,...,n - warunek konieczny

i i>0, i= 2,3,...,n-1 - warunek dostateczny

4.Częstotliwościowe kryteria

stabilności ciągłych układów

dynamicznych.

Do określenia CZ. K. S. Stosuje się kryterium Nyquista. Pozwala ono badać stabilność układu zamkniętego na podstawie przebiegu char. czę. Układu otwartego, którą można wyznaczyć analitycznie i doświadczalnie. Umożliwia ocenę odległości od granicy stabilności. Miarą jest zapas stabilny. Składa się on z zapasu fazy (określa się dla pulsacji granicznej modułu _mi z zapasu wzmocnienia(określa wzmocnienie ukł otwartego dla pulsacji granicznej fazy _)

Interpretacja zapasu stabilności

5.5 Częstotliwościowe kryteria stabilności

Kryteria algebraiczne mają wady:

- dostarczają jedynie informacji dotyczącej stabilności lub niestabilności układu,

pozostawiając kwestię odległości od granicy stabilności otwartą,

- wymagają analitycznego ujęcia transmitancji układu.

W wielu przypadkach uzyskanie opisu właściwości układu w formie jest trudne, łatwiej jest otrzymać informację o układzie w postaci np. ch-k częstotliwościowych. Najczęściej stosowane jest kryterium Nyqista, które pozwala badać stabilność układu zamkniętego na podstawie ch-ki częstotliwościowej układu otwartego. Kryterium to daje możliwość oceny odległości układu od granicy stabilności. Badanie stabilności można też przeprowadzić za pomocą logarytmicznego kryterium stabilności.

5.6 Podać warunek konieczny i wystarczający stabilności asymptotycznej układu.

Warunek konieczny i dostateczny stabilności asymptotycznej:

- wszystkie pierwiastki równania charakterystycznego, wszystkie części rzeczywiste pierwiastków zespolonych muszą być ujemne, czyli leżeć w lewej półpłaszczyźnie zmiennej zespolonej.

Układ jest stabilny nieasymptotycznie (stabilny w sensie Lapunowa), gdy oprócz pierwiastków leżących w lewej półpłaszczyźnie ma:

- jeden pierwiastek równy zero;

- pojedyncze pary pierwiastków urojonych;

- jeden pierwiastek rzeczywisty i pojedyncze pary pierwiastków urojonych.

G(j)

u(t)=U₀sint

Y(j)=Y₀e^j(t+)

y(t)=Y₀sin(t +)

U(j)=U₀e^jt

y(t)+a₁y(t)+a₀y(t)= u(t)

u(t)

y(t)

---