POLITECHNIKA ŚWIĘTOKRZYSKA Wydział Mechatroniki i Budowy Maszyn			LABORATORIUM MECHANIKI DOŚWIADCZALNEJ
Numer ćwiczenia: 6,7	Temat ćwiczenia:
Imię i nazwisko: Tomasz Żuraw		Grupa: 33 C		Ocena:	Data: 2001-01-16	Podpis:

1. Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie z techniką zmiany podatności oraz spadku potencjału, użytą do wyznaczania całki J, jak również wyznaczenie wartości J.

2. Wprowadzenie.

W zakresie plastycznym zależność pomiędzy składowymi tensorów odkształcenia i naprężenia nie jest już liniowa, bardzo często też naprężenia zależą od sposobu obciążania próbki. Rozwiązanie problemu brzegowego staje się przez to znacznie trudniejsze. Dlatego też naprężenia i odkształcenia przed frontem szczeliny można wyznaczyć wg prawa Romberga-Osgoda, metodą „całki J”:

• jest amplitudą osobliwego pola naprężeń i odkształceń przed frontem szczeliny;

• odpowiada ilości energii uwolnionej z elementu przy przyroście długości szczeliny o infinitezymalną długość da;

• jest niezmienna od konturu całkowania.

Całka J -jest równoważną różnicą energii potencjalnych dwóch prawie takich samych, identycznie obciążonych próbek różniących się od siebie jedynie długością szczeliny o infinetezymalną długość da.

gdzie:

-energia potencjalna

-energia odkształceni

-komplementarna energia odkształcenia

-praca sił zewnętrznych P na przemieszczeniu w punktach przyłożenia siły

Technika spadku potencjału pomiary krytycznej wartości całki J różni się niewiele od techniki zmiany podatności. Różnica polega tylko na innym sposobie pomiaru przyrostów długości pęknięcia. Przy pomiarze zmian długości pęknięcia techniką spadku potencjału wykorzystuje się zjawisko zmiany oporu elektrycznego próbki w trakcie zmiany jej czynnego przekroju. Przekrój zaś zmienia wraz z przyrostem długości pęknięcia. W celu przeprowadzenia pomiaru tą techniką musimy zasilić próbkę prądem o stałym natężeniu. Może to być prąd stały lub zmienny. W naszym ćwiczeniu wykorzystywać będziemy jedynie prąd stały.

- TECHNIKA ZMIANY PODATNOŚCI -

3. Schemat stanowiska.

4. Informacje dotyczące próbki.

Materiał próbki			40HM
Oznaczenie kształtu próbki			SE (B)
Norma			PN
Temperatura w czasie badania			20˚
Rm [MPa]	Re [MPa]	E [MPa]	Rozmiary próbki
						a [mm]	B [mm]	W [mm]	S [mm]
1050	900	205000	11,96	12,47	24,96	100

5. Tabela wyników pomiaru.

Nr. pomiaru	Ci [mm/KN]	Apl [Mpa]	Aspr [Mpa]	Acałk [Mpa]
1507	0,0109	2,769	11,18	13,949
1906	0,0116	5,826	14,515	20,34
2305	0,0117	10,611	16,409	27,02
2712	0,0118	19,362	15,846	35,209
3111	0,0123	30,136	13,688	43,824
3509	0,0143	38,731	13,364	52,095
3911	0,0146	48,251	12,342	60,593
4311	0,0155	56,618	11,881	68,499
4710	0,0163	65,505	11,173	76,678
5114	0,0178	73,279	11,302	84,581
5513	0,0196	81,037	10,883	91,919
5914	0,0194	89,633	8,84	98,473
6310	0,0218	96,571	8,547	105,118
6712	0,0228	103,383	7,955	111,338
7115	0,0261	109,034	7,858	116,892

6. Wyznaczenie wartości C_o.




Wyznaczona wartość minimalna podatności wyniosła C_o = 0,0109 [mm/kN] , zakładamy że jest to moment inicjacji wzrostu pęknięcia.

7. Wyznaczenie wartości a_o, b_o i a_k.

Wygrzewamy próbkę w piecu do temperatury 300˚C przez ok. 30 min, w celu zabarwienia przełomu. Po wystudzeniu dołamujemy i za pomocą mikroskopu laboratoryjnego dokonujemy pomiarów.

Początkowa długość pęknięcia a_o:

a_o1=11,879 [mm], a_o2=11,842 [mm], a_o3=11,884 [mm], a_o4=12,009 [mm], a_o5=11,966 [mm],

czyli: a_o = 11,898 [mm]

Początkowa długość pęknięcia b_o:

a_o = 11,898 [mm] , W=24,96 [mm]

b₀ = W - a_o [mm]

czyli: b₀ = 13,062 [mm]

Końcowa długość pęknięcia a_k:

∆a₁=6,838 [mm], ∆a₂=6,193 [mm], ∆a₃=6,358 [mm], ∆a₄=7,264 [mm], ∆a₅=6,760 [mm],

∆a = 6,683 [mm]

a_o = 11,898 [mm]

a_k =∆a + a_o [mm]

czyli: a_k = 18,581 [mm]

ao [mm]	bo [mm]	ak [mm]	∆a [mm]
11,898	13,062	18,581	6,683

8. Wyznaczenie wartości całki J_Ic.

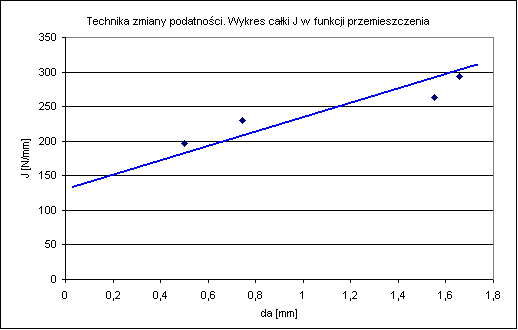
Do wyznaczenia wartości całki J_Ic bazujemy na tak zwanym „rzeczywistym przyroście długości pęknięcia”. W tym celu rysujemy linie ograniczeń prostopadłe do osi odciętych. Wartość całki odczytujemy z przecięcia linii R z osią rzędnych.

Wyznaczone wartości wynoszą:

J_Ic = 126,325 [N/mm]

9. Wnioski.

Z przeprowadzonego doświadczenia wynika, iż przybliżona wartość całki J_Ic wynosi ok. 126 [N/mm]. Przybliżona dlatego iż pomiar jest opatrzony błędami odczytu wartości a_o, a_k i b_o, jak również błędami wynikającymi z dokładności umieszczenia próbki w maszynie wytrzymałościowej oraz niewielki wpływ warunków zewnętrznych. Trudnością było również wyznaczenie momentu inicjacji przyrostu długości szczeliny. Na dokładność wpływa również fakt iż w metodzie tej liczba punktów, dla których można obliczyć przyrost szczeliny zależy od liczby odciążeń (zaczynając od tego dla którego następuje minimum podatności).

- TECHNIKA SPADKU POTENCJAŁU -

10. Schemat stanowiska.




11. Informacje dotyczące próbki.

Materiał próbki			40HM
Oznaczenie kształtu próbki			SE (B)
Norma			PN
Temperatura w czasie badania			20˚
Rm [MPa]	Re [MPa]	E [MPa]	Rozmiary próbki (przed obciążeniem)
						a [mm]	B [mm]	W [mm]	S [mm]
1050	900	205000	11,96	12,47	24,96	100

12. Wyznaczenie wartości a_o, b_o i a_k.

Wygrzewamy próbkę w piecu do temperatury 300˚C przez ok. 30 min, w celu zabarwienia przełomu. Po wystudzeniu dołamujemy i za pomocą mikroskopu laboratoryjnego dokonujemy pomiarów.

Początkowa długość pęknięcia a_o:

a_o1=11,897 [mm], a_o2=11,936 [mm], a_o3=11,849 [mm], a_o4=11,987 [mm], a_o5=11,960 [mm],

czyli: a_o = 11,928 [mm]

Początkowa długość pęknięcia b_o:

a_o = 11,928 [mm] , W=24,96 [mm]

b₀ = W - a_o [mm]

czyli: b₀ = 13,032 [mm]

Końcowa długość pęknięcia a_k:

∆a₁=8,464 [mm], ∆a₂=8,478 [mm], ∆a₃=8,175 [mm], ∆a₄=8,080 [mm], ∆a₅=8,469 [mm],

∆a = 8,333 [mm]

a_o = 11,928 [mm]

a_k =∆a + a_o [mm]

czyli: a_k = 20,261 [mm]

ao [mm]	bo [mm]	ak [mm]	∆a [mm]
11,898	13,032	20,261	8,333

13. Wyznaczenie wartości całki J_Ic.














Wyznaczone wartości wynoszą:

J_Ic = 181,807 [N/mm]

14. Wnioski.

Z doświadczenia wynika, iż przybliżona wartość całki wynosi ok. 182 [N/mm]. Wartość ta jest opatrzona błędem, jaki mógł wyniknąć z powodu utrudnionego odczytu wartości momentu inicjacji początku procesu rozwarcia pęknięcia z wykresu, ze względu na bardzo duże zagęszczenie punktów pomiarowych.

Na podstawie otrzymanych wyników możemy zauważyć, że metoda badania odporności na pękanie przez wyznaczenie krytycznej wartości całki J_ic jest dosyć dokładną metodą. Jednakże nie można jej stosować dla wszystkich materiałów, a także dla każdego przypadku pękania.

Metoda całki J podlega szeregowi ograniczeń, dlatego nie jest metoda uniwersalną. Na podstawie przeprowadzonych badań możemy zauważyć że wartości całki J obliczona za pomocą różnych metod dla tego samego materiału nie są takie same i mogą się różnić o dość duże wartości.

Mechdoś_5




Jic

---