Ćwiczenie numer: 2 Data oddania ćwiczenia: Temat: Struktury drzewiaste

I. Treść zadania:

1. Zbudować z losowa generowanych elementów listę oraz drzewo BST. Pomierzyć czasy funkcji ilości elementów dla:

1. czasu konstrukcji struktury

2. sumarycznego czasu poszukiwania 1000 wybranych elementów .

3. czasu usuwania całej struktury.

2. Zastosować procedurę wyważania drzewa tak aby utworzyć drzewo dokładnie wyważone oraz drzewo AVL wyważone. Dla wszystkich czterech struktur porównać czasy budowy, poszukiwania losowych elementów oraz usuwania całej struktury. Wyniki przedstawic na wykresie.

3. Omówić przeglądanie drzewa binarnego : wzdłużnie, poprzecznie i wstecznie.

4. Sformułować wnioski ogólne dotyczące struktur i przydatność danych struktur do praktycznych zastosowań.

II. Wstępna analiza.

1. Lista.

Lista to struktura, w której elementy są ułożone w liniowym porządku. Jednak w przeciwieństwie do tablicy, w której porządek wyznaczają jej indeksy - tutaj określają go wskaźniki.

Lista jest skończonym ciągiem elementów: l=[x₁, x₂, ..., x_n]. Skrajne elementy listy x₁ i x_n nazywają się końcami listy, a wielkość |l|=n długością listy. Szczególnym przypadkiem listy jest lista nie zawierająca żadnego elementu wtedy nazywamy ją listą pustą: l=[ ].

Elementami listy mogą być liczby, znaki, rekordy lub wskaźniki odnoszące się do dowolnych danych .Lista to struktura dynamiczna oznacza to więc, że pamięć dla kolejnych elementów jest przydzielana w momencie ich dodawania, ponad to lista nie wymaga ciągłej przestrzeni pamięciowej dla całej struktury.

Przykład listy:

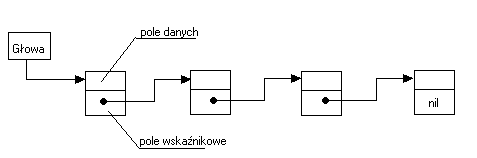
Lista jednokierunkowa zbudowana jest z rekordu, który składa się z pola na dane i wskaźnika na następny element tego samego typu, a na ostatnim elemencie wskaźnik ten przyjmuje wartość NIL. Rekord reprezentujący listę składa się z dwóch pól:

• pola wskaźnika na następny element listy (na rys. „pole wskaźnikowe”);

• pola danych typu liczbowego (na rys. „pole danych”)

Jest to struktura o sekwencyjnym dostępie do danych. Oznacza to że szukając jakiegoś elementu w liście musimy zacząć poszukiwania od pierwszego elementu listy i po kolei przesuwać się w kierunku końca listy.

Dla zwiększenia szybkości dostępu do końca listy można wprowadzić dodatkowy element informacyjny który na bieżąco będzie wskazywać adres ostatniego elementu listy. W klasycznym opisie struktury listowej element ten nie występuje, warto jednak w praktycznych zastosowaniach wykorzystać tę drobną modyfikację ponieważ usprawnia wszystkie operacje wymagające dostępu do końcowego elementu listy. Mogą to być czynności związane z usunięciem lub dodaniem nowego elementu lub z odczytem danych przechowywanych w ostatnim rekordzie listy.

Podstawowymi operacjami jakie możemy wykonywać na liście są :

• dodanie elementu

• dodanie elementu z sortowaniem

• usunięcie elementu

• szukanie elementu.

WYSZUKIWANIE W LIŚCIE ELEMENTU .

Jest to operacja bardzo często wykonywana na liście - wyszukuje się element o danej wartości x. Tak jak w strukturach plikowych, przeszukiwanie jest tutaj czysto sekwencyjne. Kończy się ono po odnalezieniu szukanego elementu lub osiągnięciu końca listy.

USUNIĘCIE ELEMENTU Z LISTY

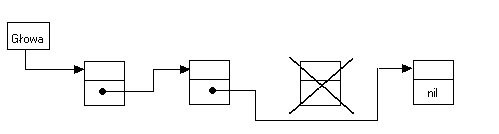
Jest to operacja polegająca na usunięciu elementu o wartości x. W ten sposób, że element poprzedzający usuwany element wskazuje nie na niego ale na następny element z listy. A element usuwany zostanie usunięty z pamięci za pomocą polecenia dispose.

2. Drzewo BST.

Drzewa przeszukiwań binarnych, w skrócie BST(ang. Binary Search Trees), to struktury , na których możliwe jest wykonywanie różnych operacji właściwych dla dynamicznych zbiorów takich jak: szukanie, wstawianie, usuwanie.

Podczas wykonywania tych operacji na drzewach binarnych wymagany jest czas proporcjonalny do wysokości drzewa. Gdy mamy pełne drzewo o n - węzłach to w/w operacje będą działać w najgorszym przypadku w czasie Θ(log n). Może jednak wystąpić sytuacja, gdzie drzewo składa się z jednej gałęzi o długości n, to w/w operacje w pesymistycznym przypadku wymagają czasu Θ( n ).

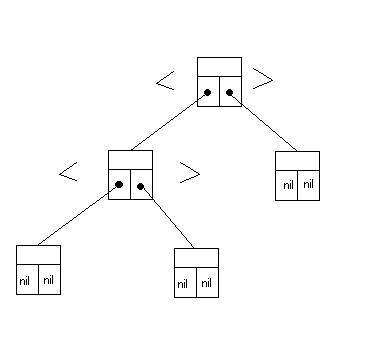
Drzewo BST ma strukturę, którą realizuje się za pomocą struktur danych z dowiązaniami, w której każdy węzeł jest obiektem. Oprócz pola z zawierającego dane zawiera również pola lewy i prawy, będące wskaźnikami na odpowiednie pola w lewej lub prawej gałęzi.

WŁASNOŚĆ DRZEWA BST.

Klucze w drzewie BST są przechowywane w taki sposób, aby spełniona była własność :Niech x będzie węzłem drzewa BST. Jeśli y jest węzłem znajdującym się w lewym poddrzewie węzła x , to key[y] ≤ key[x].Jeśli y jest węzłem znajdującym się w prawym poddrzewie węzła x, to key[x] ≤ key[y].Własność drzewa BST umożliwia wypisanie wszystkich znajdujących się w nim kluczy w sposób uporządkowany za pomocą prostych algorytmów rekurencyjnych, o których będzie mowa później.

WYSZUKIWANIE W DRZEWACH BST.

Szukając w drzewie BST węzła zawierającego dany klucz wykorzystujemy procedurę, która rozpoczyna wyszukiwanie w korzeniu i schodzi po ścieżce w dół drzewa. Dla każdego napotkanego węzła x porównuje klucz k z wartością key[x]. Gdy wartości te są równe poszukiwanie się kończy. Jeśli k jest mniejsze niż key[x] - to dalsze przeszukiwanie przebiega już tylko w lewym poddrzewie węzła x , ponieważ z własności drzewa BST wynika, że k nie może znajdować się w prawym poddrzewie. Jeśli k jest większe niż key[x] - to dalsze przeszukiwanie zostaje ograniczone do prawego poddrzewa węzła x Liczba odwiedzonych węzłów wynosi O( h ), gdzie h jest wysokością drzewa. Procedura wyszukiwania zostanie zakończona gdy wartość klucza k będzie równa wartości key[x] lub gdy zostanie osiągnięty koniec drzewa.

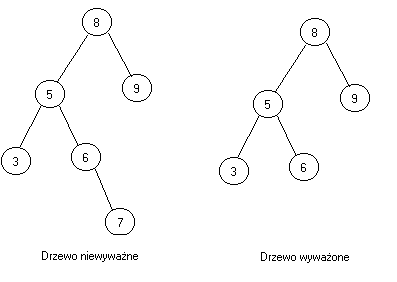
3. Drzewo dokładnie wyważone.

Jest to drzewo, które spełnia założenie: dla każdego węzła gałęzie w jego podwęzłach mogą się różnić co najwyżej o 1. Algorytm budujący takie drzewo jest bardzo skomplikowany dlatego dla uproszczenia elementy wstawiane do drzewa są pobierane z posortowanej tablicy. Zaletą takiego drzewa jest to, że ma ono bardzo małą wysokość w stosunku do innych drzew ze względu na dokładne wypełnienie całej struktury.

4. 
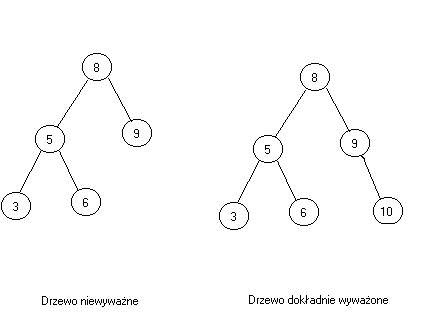
   Drzewo AVL wyważone.

Z przeprowadzonych badań wynika, że procedura wstawiania, która zawsze przywraca dokładnie wyważona strukturę drzewa jest nieopłacalna, ponieważ czynność ta jest operacją dość skomplikowaną .

Należało więc znaleźć metodę bardziej efektywną . Znaleziono takie rozwiązanie opierając się na definicji wyważenia, którą zaproponowali Adelson-Velskii i Landis. Kryterium to brzmiało następująco: Drzewo jest wyważone wtedy i tylko wtedy, gdy dla każdego węzła wysokości dwóch jego poddrzew różnią się co najwyżej o 1.

Drzewa spełniające ten warunek są często nazywane drzewami AVL, lub inaczej drzewami wyważonymi .Formuła ta jest nie tylko prosta, ale także prowadzi do łatwej w obsłudze procedury wyważającej drzewo. Średnia długość drogi poszukiwania jest praktycznie identyczna z odpowiednią długością w drzewie dokładnie wyważonym.

W najbardziej pesymistycznym przypadku, na drzewie wyważonym można wykonywać w O ( log n ) jednostkach czasu takie operacje jak:

• lokalizacja węzła o danym kluczu;

• wstawienie węzła o danym kluczu;

• usunięcie węzła o danym kluczu.

Sformułowanie to oparte jest na twierdzeniu AVL , które gwarantuje, że niezależnie od liczby węzłów drzewo wyważone nie będzie nigdy wyższe o więcej niż 45 % od swego dokładnie wyważonego odpowiednika.

Jeżeli oznaczymy wysokość wyważonego drzewa o n węzłach przez h_z(n), to

log ( n + 1) ≤ h_z(n) ≤ 1,4404 ∙ log ( n + 2 ) - 0,328.

METODA WYWAŻANIA.

Metoda wstawiania do drzewa wyważonego rozróżnia trzy przypadki:

1. h_l = h_p L i P stają się drzewami o różnej wysokości, ale kryterium wyważenia jest w dalszym ciągu spełnione;

2. h_l < h_p L i P uzyskują jednakową wysokość, wyważanie drzewa nawet się poprawia;

3. h_l > h_p kryterium wyważenia nie jest spełnione i drzewo musi zostać przebudowane;

Algorytm wstawiania i wyważania zależy od sposobu przechowywania informacji o wyważeniu drzewa. Krańcowe rozwiązanie polega na trzymaniu wszystkich informacji o wyważeniu drzewa ukrytych w samej strukturze drzewa. W tym przypadku współczynnik wyważenia musi być wyznaczany za każdym razem od nowa, jeżeli ulegnie zmianie w wyniku wstawiania, co prowadzi do znacznie gorszej efektywności. Drugą skrajnością jest przypisanie współczynnika wyważenia każdemu węzłowi i pamiętanie go wraz z węzłem.

Proces wstawiania węzła to praktycznie trzy etapy:

a) Idź po ścieżce przeszukiwania drzewa aż do stwierdzenia, że klucza nie ma w drzewie.

b) Wstaw nowy węzeł i wyznacz wynikający z tego współczynnik wyważenia.

c)Cofaj się po ścieżce przeszukiwania i sprawdzaj w każdym węźle współczynnik wyważenia

5. Metody przeszukiwania drzew binarnych.

Wszystkie te metody pozwalają się zapisać jako procedury rekurencyjne co jest ich niewątpliwą zaletą.

1. Wzdłużna - polega na tym, że najpierw odwiedzamy korzeń a później jego poddrzewa. Przykładowa procedura w Pascalu :

procedure wzdluz(var e:element);

begin

if e=nil then exit;

write(' ',e^.dana);

wzdluz(e^.lewy);

wzdluz(e^.prawy);

end;

2. Poprzeczna - polega na tym, że najpierw odwiedzamy lewe poddrzewo następnie korzeń a na końcu prawe poddrzewo (zawsze najbardziej lewą). Przykładowa procedura w Pascalu:

procedure poprzeczne(var g:element);

begin

if g=nil then exit;

poprzeczne(g^.lewy);

write(' ',g^.dana);

poprzeczne(g^.prawy);

end;

3. Wsteczna - polega na tym, że najpierw odwiedzamy lewe poddrzewo następnie prawe poddrzewo na końcu korzeń . Przykładowa procedura w Pascalu:

procedure wstecz(var f:element);

begin

if f=nil then exit;

wstecz(f^.lewy);

wstecz(f^.prawy);

write(' ',f^.dana);

end;

III. Listingi programów.

1. Program Lista :

program lista;

uses

crt,Dos;

const n=25000;

const w=1000; {ilosc usuwanych i szukanych elementow}

const pod=0; {wyswietlanie elementow}

type

wsk=^typwsk;

typwsk=record

id:integer;

nast:wsk;

end;

var

element,wartownik,glowa,pp,qq:wsk;

t:array[1..N] of INTEGER;

pomocnicza:array[1..100] of real;

trafione,temp,los,ile,a,x,b,k:word;

Poczatek,koniec :LongInt;

suma:real;

nazwa:string[12];

f:text;

nie_znalazlem:boolean;

Function WlaczTimer :LongInt;

Var Reg :Registers;

Znacznik :Byte;

Begin

Znacznik:=0;

Reg.AH:=$83;

Reg.AL:=0;

Reg.CX:=$7FFF;

Reg.DX:=$FFFF;

Reg.BX:=Ofs(Znacznik);

Reg.ES:=Seg(Znacznik);

Intr($15,Reg);

WlaczTimer:=$7FFFFFFF;

End;

Function WylaczTimer :LongInt;

Var Reg :Registers;

Begin

WylaczTimer:=MemL[$0040:$009C];

Reg.AH:=$83;

Reg.AL:=1;

Intr($15,Reg);

End;

Function CzasWykonania :Real;

Var Czas :Real;

Begin

Czas:=(Poczatek-koniec);

CzasWykonania:=Czas;

End;

function sprawdz(k,liczba:integer) :boolean;

var jest:boolean;

liczba2:integer;

begin

liczba2:=1;

repeat

if t[liczba2]=liczba then jest:=true else jest:=false;

liczba2:=liczba2+1;

until ((k=liczba2) or (jest=true));

sprawdz:=jest;

end;

procedure Tablica;

var

tab,K,liczba:integer;

begin

t[1]:=random(65000);

k:=2;

writeln('Trwa losowanie tablicy - to moze troche potrwac. Idzi na kawe!!!');

writeln;

repeat

liczba:=random(65000);

if sprawdz(k,liczba)=false then

begin

T[k]:=liczba;

k:=k+1;

end;

if (k mod 500)=0 then write('.');

until k>n;

end;

procedure wyswietl;

var k:integer;

begin

for k:=1 to n-ile do

write(' ',t[k]:2);

WRITELN;

end;

procedure przegladaj;

var

q:wsk;

begin

q:=glowa^.nast;

writeln;

repeat

write(' ',q^.id);

q:=q^.nast;

until q=nil;

end;

procedure szukaj(x:integer; var p,q:wsk;lista:wsk); {szuka elementu o wartosci x}

begin

q:=lista; wartownik^.id:=x; p:=q^.nast;

while p^.id<x do begin q:=p; p:=q^.nast; end;

end;

procedure wstaw(x:integer;lista:wsk);

var p,q:wsk;

begin

szukaj(x,p,q,lista);

new(p);p^.id:=x;

p^.nast:=q^.nast;

q^.nast:=p;

end;

procedure usun(x:integer;lista:wsk);{usuwa element o wartosci x}

var

p,q:wsk;

begin

szukaj(x,p,q,lista);

if (p<>nil)and(p^.id=x)then

begin

q^.nast:=p^.nast;

p^.nast:=nil;

dispose(p);

trafione:=trafione+1;

end;

end;

procedure usun_calosc2;

var

pom,pom2:wsk;

begin

pom2:=glowa;

repeat

if pom2<>nil then

begin

pom:=pom2;

pom2:=pom2^.nast;

dispose(pom);

end;

until pom2=nil;

end;

{*****************}

begin

randomize;

clrscr;

nie_znalazlem:=false;

writeln(' Program Lista ');

writeln;

writeln('Podaj nazwe pliku, do ktorego beda zapisywane wyniki:');

writeln('jesli enter to lista.txt');

readln(nazwa);

if nazwa=''then nazwa:='lista.txt';

Assign(f,nazwa);

rewrite(f);

tablica;

if pod=1 then wyswietl;

poczatek:= WlaczTimer;

koniec:=wylaczTimer;

writeln;

writeln(' Tablica | Budowanie | Szukanie los | Usuwamie los | Usuwanie calej');

writeln(f,' Tablica | Budowanie | Szukanie los | Usuwamie los | Usuwanie calej');

writeln;

ile:=n;

repeat

begin

ile:=ile-w;

{------budowanie listy------}

write(n-ile:10);

write(f,n-ile:10);

poczatek:= WlaczTimer;

new(glowa);

element:=glowa;

element^.nast:=NIL;

for k:=1 to n-ile do

begin

a:=t[k];

wstaw(a,element);

end;

koniec:=wylaczTimer;

write(czaswykonania/1000000:15:5);

write(f,czaswykonania:15:0);

{-------szukanie------}

if pod=1 then przegladaj;

suma:=0;

for k:=1 to w do

begin

los:=random(65000);

poczatek:= WlaczTimer;

szukaj(los,pp,qq,element);

koniec:=wylaczTimer;

suma:=suma+czaswykonania;

end;

write(suma/1000000:15:5);

write(f,suma:15:0);

{-------usuwanie losowych elementow-------}

if pod=1 then przegladaj;

trafione:=0;

suma:=0;

for k:=1 to 5000 do

begin

los:=random(n+n);

poczatek:= WlaczTimer;

usun(los,element);

koniec:=wylaczTimer;

suma:=suma+czaswykonania;

end;

write(suma/1000000:15:5);

write(f,suma:15:0);

usun_calosc2; {usuwanie calej }

new(glowa); {i budowanie od nowa}

element:=glowa;

element^.nast:=NIL;

for k:=1 to n-ile do

begin

a:=t[k];

wstaw(a,element);end;

{------------usuwanie calej listy-----------}

poczatek:= WlaczTimer;

usun_calosc2;

koniec:=wylaczTimer;

write(czaswykonania/1000000:15:5);

writeln;

write(f,czaswykonania:20:0);

writeln(f);

if pod=1 then przegladaj;

end;

until ile=0;

close(f);

writeln;

writeln('********KONIEC********');

writeln;

sound(1000);

delay(100);

nosound;

readln;

end.

2. Program Drzewo:

program drzewo;

uses crt,graph,dos;

const n=25000;

const krok=1000;

const wys=false;

const roz_los=65000;

type

element=^tree;

tree=record

dana:word;

lewy:element;

prawy:element;

wywaz:integer;

end;

var

t:array[1..n] of word;

glowa:element;

flaga,hit,mis,los,ile,c:word;

suma,poczatek,koniec:real;

nazwa:string[13];

f:text;

bool:boolean;

Function WlaczTimer :LongInt;

Var Reg :Registers;

Znacznik :Byte;

Begin

Znacznik:=0;

Reg.AH:=$83;

Reg.AL:=0;

Reg.CX:=$7FFF;

Reg.DX:=$FFFF;

Reg.BX:=Ofs(Znacznik);

Reg.ES:=Seg(Znacznik);

Intr($15,Reg);

WlaczTimer:=$7FFFFFFF;

End;

Function WylaczTimer :LongInt;

Var Reg :Registers;

Begin

WylaczTimer:=MemL[$0040:$009C];

Reg.AH:=$83;

Reg.AL:=1;

Intr($15,Reg);

End;

Function CzasWykonania :Real;

Var Czas :Real;

Begin

Czas:=(Poczatek-koniec);

CzasWykonania:=Czas;

End;

function sprawdz(k,liczba3:word) :boolean;

var jest:boolean;

liczba2:word;

begin

liczba2:=0;

repeat

liczba2:=liczba2+1;

if t[liczba2]=liczba3 then jest:=true else jest:=false;

until ((k=liczba2) or (jest=true));

sprawdz:=jest;

end;

procedure Tablica;

var

K,liczba:word;

begin

t[1]:=random(roz_los);

k:=2;

writeln('Trwa losowanie tablicy - to moze troche potrwac. Idzi na kawe!!!');

writeln;

repeat

repeat

liczba:=random(roz_los);

until liczba<>0;

if sprawdz(k,liczba)=false then

begin

T[k]:=liczba;

k:=k+1;

end;

if (k mod 500)=0 then write('.');

until k>n;

end;

procedure wyswietl;

var k:integer;

begin

for k:=1 to n-ile do

write(' ',t[k]:2);

WRITELN;

end;

procedure usun(var b:element);

begin

if b=nil then exit;

usun(b^.lewy);

usun(b^.prawy);

dispose(b);

b:=nil;

end;

procedure buduj (index:word);

var

pom:element;

begin

repeat

if glowa=nil then

begin

new(glowa);

glowa^.dana:=t[1];

glowa^.lewy:=nil;

glowa^.prawy:=nil;

end;

pom:=glowa;

repeat

if pom^.dana>t[index] then

begin

if pom^.lewy<>nil then pom:=pom^.lewy;

end

else

if pom^.dana<t[index] then

begin

if pom^.prawy<>nil then pom:=pom^.prawy;

end

else

if pom^.dana=t[index] then begin writeln('ERROR !!!'); halt; end;

until ((pom^.dana>t[index]) and (pom^.lewy=nil))or((pom^.dana<t[index]) and (pom^.prawy=nil));

if pom^.dana>t[index] then

begin

new(pom^.lewy);

pom:=pom^.lewy;

pom^.dana:=t[index];

pom^.prawy:=nil;

pom^.lewy:=nil;

end

else

begin

new(pom^.prawy);

pom:=pom^.prawy;

pom^.dana:=t[index];

pom^.prawy:=nil;

pom^.lewy:=nil;

end;

inc(index);

until index>n-ILE;

end;

procedure buduj2 (elem:word);

var

pom:element;

begin

pom:=glowa;

repeat

if glowa=nil then

begin

new(glowa);

glowa^.dana:=elem;

glowa^.lewy:=nil;

glowa^.prawy:=nil;

exit;

end;

if pom^.dana>elem then

begin

if pom^.lewy<>nil then pom:=pom^.lewy;

end;

if pom^.dana<elem then

begin

if pom^.prawy<>nil then pom:=pom^.prawy;

end;

until ((pom^.dana>elem) and (pom^.lewy=nil)) {>=}

or ((pom^.dana<elem) and (pom^.prawy=nil));{<=}

if pom^.dana>elem then

begin

new(pom^.lewy);

pom:=pom^.lewy;

pom^.dana:=elem;

pom^.prawy:=nil;

pom^.lewy:=nil;

end

else

begin

new(pom^.prawy);

pom:=pom^.prawy;

pom^.dana:=elem;

pom^.prawy:=nil;

pom^.lewy:=nil;

end;

end;

procedure SZUKAJ(x:word);

var

pom:element;

begin

if glowa=nil then EXIT;

pom:=glowa;

repeat

if pom^.dana>x then

begin

if pom^.lewy<>nil then pom:=pom^.lewy;

end

else

if pom^.dana<x then

begin

if pom^.prawy<>nil then pom:=pom^.prawy;

end;

if pom^.dana=x then begin hit:=hit+1;exit; end

until ((pom^.dana>x) and (pom^.lewy=nil)) or ((pom^.dana<x) and (pom^.prawy=nil));

mis:=mis+1;

end;

{######## rysowanie drzewka ##########}

procedure piszDgra(x,y,delta:word;gdzie:element);

var

s:string[10];

procedure pisz(x,y,delta:word;gdzie:element);

begin

if gdzie=nil then exit;

str(gdzie^.dana,s);

OutTextXY(x-6,y,s);

if gdzie^.lewy<>nil then begin

line(x,y+10,x-delta,y+30);

pisz(x-delta,y+35,delta div 2,gdzie^.lewy);

end;

if gdzie^.prawy<>nil then begin

line(x,y+10,x+delta,y+30);

pisz(x+delta,y+35,delta div 2,gdzie^.prawy);

end;

end;

var

grDriver,grfriver,err: Integer;

begin

grDriver := Detect;

grfriver := 6;

InitGraph(grDriver,grfriver,'');

Err := GraphResult;

if Err = grOk then

begin { Do graphics }

ClearDevice;

pisz(319,1,159,gdzie);

repeat until keypressed;readkey;

{

delay(5000);

}

CloseGraph;

end;

end;

procedure poszukaj_wzdluz(var e:element);

begin

if e=nil then exit;

write(' ',e^.dana);

poszukaj_wzdluz(e^.lewy);

poszukaj_wzdluz(e^.prawy);

end;

procedure poszukaj_wstecz(var f:element);

begin

if f=nil then exit;

poszukaj_wstecz(f^.lewy);

poszukaj_wstecz(f^.prawy);

write(' ',f^.dana);

end;

procedure poszukaj_poprzeczne(var g:element);

begin

if g=nil then exit;

poszukaj_poprzeczne(g^.lewy);

write(' ',g^.dana);

poszukaj_poprzeczne(g^.prawy);

end;

{==============avl==================}

procedure wywaz(x:word;var p:element;var h:boolean);

var

p1,p2:element;

begin

if p=nil then

begin

new(p);

h:=true;

with p^ do

begin

dana:=x;

lewy:=nil;

prawy:=nil;

wywaz:=0;

end;

end

else

if x<p^.dana then

begin

wywaz(x,p^.lewy,h);

if h then

case p^.wywaz of

1: begin

p^.wywaz:=0;

h:=false;

end;

0: p^.wywaz:=-1;

-1: begin {pojedyncza zamiana LL}

p1:=p^.lewy;

if p1^.wywaz=-1 then

begin

p^.lewy:=p1^.prawy;

p1^.prawy:=p;

p^.wywaz:=0;

p:=p1;

end

else

begin {podwojna zamiana LP}

p2:=p1^.prawy;

p1^.prawy:=p2^.lewy;

p2^.lewy:=p1;

p^.lewy:=p2^.prawy;

p2^.prawy:=p;

if p2^.wywaz=-1 then p^.wywaz:=1 else p^.wywaz:=0;

if p2^.wywaz=1 then p1^.wywaz:=-1 else p1^.wywaz:=0;

p:=p2;

end;

p^.wywaz:=0;

h:=false;

end

end

end

else

if x>p^.dana then

begin

wywaz(x,p^.prawy,h);

if h then

case p^.wywaz of

-1:begin

p^.wywaz:=0;

h:=false;

end;

0: p^.wywaz:=1;

1: begin

p1:=p^.prawy;

if p1^.wywaz=1 then

begin

p^.prawy:=p1^.lewy;

p1^.lewy:=p;

p^.wywaz:=0;

p:=p1;

end

else

begin

p2:=p1^.lewy;

p1^.lewy:=p2^.prawy;

p2^.prawy:=p1;

p^.prawy:=p2^.lewy;

p2^.lewy:=p;

if p2^.wywaz=1 then p^.wywaz:=-1 else p^.wywaz:=0;

if p2^.wywaz=-1 then p1^.wywaz:=1 else p1^.wywaz:=0;

p:=p2;

end;

p^.wywaz:=0;

h:=false;

end;

end

end

else

h:=false;

end;

{-----------------AVL dok -----------------------------------}

procedure quicksort(l,p:word);

var

i,j,srodek,temp:word;

begin

srodek:=(l+p) div 2;

i:=l;j:=p;

repeat

while (t[i]<=t[srodek]) and (i<>srodek) do i:=i+1;

while (t[j]>=t[srodek]) and (j<>srodek) do j:=j-1;

if i<j then begin temp:=t[i];t[i]:=t[j];t[j]:=temp;end;

if i=srodek then srodek:=j else

if j=srodek then srodek:=i;

until j=i;

if i>l then Quicksort(l,i-1);

if j<p then Quicksort(i+1,p)

end;

procedure avl_dok(l,p:word);

{var srodek:word;}

begin

{srodek:=(p+l) div 2;}

if l+1=p then exit;

buduj2(t[(l+p) div 2]);

avl_dok(l,(l+p) div 2);

avl_dok((l+p) div 2,p);

end;

{ Program glowny }

begin

randomize;

clrscr;

ile:=n;

writeln(' Drzewo BST/AVL ');

writeln('podaj nazwe pliku, do ktorego beda zapisywane wyniki:');

writeln('jesli enter to drzewo.txt');

readln(nazwa);

if nazwa=''then nazwa:='DRZEWO.txt';

Assign(f,nazwa);

rewrite(f);

poczatek:= WlaczTimer;

koniec:=wylaczTimer;

tablica;

writeln;

writeln(' Tablica | Budowanie | Szukanie los | Hit | Miss | Usuwamie calej');

writeln(f,' Tablica | Budowanie | Szukanie los | Usuwamie calej');

flaga:=0;

repeat

ile:=n;

if flaga=0 then

writeln('­---------------------------------BST-----------------------------------­');

repeat

ile:=ile-krok;

mis:=0;

hit:=0;

{wyswietl;}

writeln;

write(n-ile:12);

writeln(f);

write(f,n-ile:12);

if flaga=0 then

begin

poczatek:= WlaczTimer;

buduj(2);

koniec:=wylacztimer;

end;

if wys=true then piszDgra(300,20,150,glowa);

if flaga=1 then

begin

poczatek:= WlaczTimer;

for c:=1 to n-ile do

wywaz(t[c],glowa,bool);

koniec:=wylacztimer;

if wys=true then piszDgra(300,20,150,glowa);

end;

if flaga=2 then

begin

quicksort(1,n-ile);

if wys=true then piszDgra(300,20,150,glowa);

poczatek:= WlaczTimer;

avl_dok(1,n-ile); {tu by sie przydala proc avl dok}

koniec:=wylacztimer;

if wys=true then piszDgra(300,20,150,glowa);

end;

koniec:=wylacztimer;

write(f,Poczatek-koniec:15:0);

write((Poczatek-koniec)/1000000:15:8);

suma:=0;

for c:=1 to krok do

begin

los:=random(roz_los);

poczatek:= WlaczTimer;

szukaj(los);

koniec:=wylacztimer;

suma:=suma+czaswykonania;

end;

WRITE(suma/1000000:17:5);

WRITE(F,suma:15:0);

write(hit:7);

write(mis:5);

poczatek:= WlaczTimer;

usun(glowa);

koniec:=wylacztimer;

write(f,Poczatek-koniec:15:0);

write((Poczatek-koniec)/1000000:15:5);

until ile=0;

flaga:=flaga+1;

if flaga=1 then

begin

writeln;

writeln(f);

writeln('­---------------------------------AVL-----------------------------------­');

end;

if flaga=2 then

begin

writeln;

writeln(f);

writeln('­------------------------------AVL dokladny-----------------------------­');

end;

until flaga>2;

close(f);

writeln;

writeln('********KONIEC********');

writeln;

sound(1000);

delay(100);

nosound;

end.

IV. Tabele pomiarów.

V. Wykresy.

V. Wnioski.

Po przeprowadzeniu badań doszedłem do następujących wniosków:

Podczas wszystkich pomiarów lista za każdym razem wypadała bardzo kiepsko, co było spowodowane tym, że podczas wyszukiwania elementu na posortowanej liście wykonuje średnio N/2 porównań. W przypadku pesymistycznym, gdy jako ciąg wejściowy podawana jest tablica posortowana algorytm za każdym razem wykonuje N porównań. Jedynie usuwanie przebiega dość szybko, co jest spowodowane tym, że każdorazowo jest usuwany ostatni element i za każdym usunięciem lista stawała się krótsza. Niewątpliwą zaletą listy jest to, że bardzo proste są algorytmy ją obsługujące, takie jak przeszukiwanie, budowanie i co najważniejsze dodawanie nowego elementu. W przypadku drzewa AVL i dokładnie wyważonego dodanie nowego elementu jest przeważnie związane z wyważeniem całej struktury. Jak wskazują badania empiryczne to co druga dołączona do struktury liczba zmusza algorytm to ponownego wyważenia drzewa co raczej do zalet zaliczyć nie można.

Drzewo BST w pomiarach było znacznie szybsze od listy jednak wolniejsze od drzewa dokładnie wyważonego i AVL . Przewaga drzewa nad listą najbardziej jest zauważalna podczas wyszukiwania, gdzie czas wyszukiwania w drzewie jest znacznie lepszy. Jest to spowodowane, że wyszukiwanie w drzewie binarnym odbywa się za pomocą klucza, dzięki, któremu maksymalna liczba porównań jest równa wysokości drzewa. W drzewie BST w wysokości drzewa jest pewną pułapką ponieważ jeśli jako ciąg wejściowy zostanie podany ciąg liczb posortowanych (tablica posortowana) lub prawie posortowanych to drzewo będzie listą albo drzewem o bardzo dużych różnicach w wysokościach poszczególnych gałęziach.

Przeciwdziałaniem takim sytuacją, które bardzo pogarszają efektywność drzewa są drzewa dokładnie wyważone. Te drzewa mają zawsze równą liczbę gałęzi w lewym i prawym węźle drzewa z dokładnością do 1. Wysokość drzewa można łatwo oszacować, gdyż zakładając, że X będzie oznaczać kolejne poziomy drzewa to zależność X² określa nam liczbę elementów jakie może pomieścić każdy z poziomów. Jak widać podczas budowania drzewa dokładnie wyważonego wysokość rośnie bardzo powoli. Wadą drzew dokładnie wyważonych jest to, że algorytm wyważania jest bardzo skomplikowany. Dla uproszczenia w moim programie przy budowie tego drzewa użyłem uproszczonego algorytmu polegającego nie na ciągłym wyważaniu drzewa ale na posortowaniu całej tablicy a następnie odpowiednim umieszczaniu elementów w strukturze drzewa.

Alternatywą dla drzewa dokładnie wyważonego jest drzewo AVL, gdzie liczba węzłów w lewym i prawym poddrzewie jest taka sama z dokładnością do 1( tzn. różnica wysokości pomiędzy nimi może wynosić co najwyżej jeden). Algorytm budowy drzewa AVL nie jest tak skomplikowany jak dokładnie wyważonego a jego efektywność jest porównywalna z dokładnie wyważonym . Niezbyt wyraźnie ale widać to na wykresie „szukanie 1000 losowych elementów”, gdzie wyszukiwanie w AVL jest szybsze od wyszukiwania w drzewie BST a nieznacznie gorsze od wyszukiwania w drzewie dokładnie wyważonym.

Wykres przedstawiający wyszukiwanie elementów w strukturach jest nieczytelny przy porównywaniu struktur drzewiastych, gdyż czas sumaryczny szukania 1000 elementów okazuje się zbyt mały a co za tym idzie mniej dokładny, aby uzyskać czasy bardziej zbliżone do średnich a mniej losowych należało by szukać 5000 a nawet 10000 elementów. Myślę jednak, że pomiar ten spełnia swoje zadanie bo pokazuje znaczącą przewagę drzew nad listą.

Praktyczne zastosowanie omawianych struktur:

Lista:

Zastosowanie:

• reprezentowanie zbiorów dynamicznych

Cechy listy:

• mała zajętość pamięci, praktycznie ograniczona do długości listy;

• procedury obsługujące listę są proste np.: wyszukiwanie w pętli, a co za tym idzie nie zajmują pamięci;

• zmianę lub usunięcie elementu z listy można dokonać stosunkowo niedużym kosztem;

• umożliwia wykonywanie takich operacji jak:

• wyszukiwanie elementu

• szukanie minimum i maksimum

• wstawianie nowych elementów

• usuwanie elementów

Drzewo :

Zastosowanie:

- słownik

- kolejka priorytetowa;

Cechy listy:

• duża zajętość pamięci ;

• procedury wykorzystujące rekurencję np.: podczas przeszukiwania

• w drzewach dokładnie wyważonych i AVL dość skomplikowane procedury wstawiania i wyważania

- podobne jak w liście można wykonywać takie operacje jak :

• wyszukiwanie elementu

• szukanie minimum i maksimum

• wstawianie nowych elementów

• usuwanie elementów

2

20

---