POLITECHNIKA ŚLĄSKA W GLIWICACH

WYDZIAŁ ELEKTRYCZNY

LABORATORIUM ROBOTYKI

Temat ćwiczenia:

Przekształcenia jednorodne w robotyce

Wykonali: Pióro Klaudia

Kupski Michał

Siedlarek Damian

Domalik Patryk

Zieliński Marcin

Grupa: KSS 1

Sekcja: 5

1. Cel ćwiczenia

Celem ćwiczenia było zapoznanie się z zagadnieniem ruchu sztywnego ( jest to związek pomiędzy układem O x₀ y₀ z₀ i układem O x₁ y₁ z₁ wyrażony jako kombinacja obrotu i przesunięcia).

2. Przebieg ćwiczenia

W pierwszej części naszego ćwiczenia musieliśmy wyznaczyć macierze, które w pełni zdefiniuje nam położenie i orientację wektora w przestrzeni trójwymiarowej. Aby lepiej zapoznać się z tym tematem rozważmy następującą reprezentację macierzową:

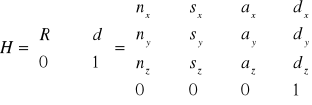
W przedstawionym powyżej równaniu, n=(n_x n_y n_z)^T jest wektorem reprezentującym kierunek osi O₁x₁ w układzie O x₀ y₀ z_0, s=(s_x s_y s_z)^T reprezentuje kierunek osi O₁y₁, natomiast a=(a_x a_y a_z)^T reprezentuje kierunek osi O₁z₁. Wektor d=(d_x d_y d_z)^T jest reprezentacją wektora od początku O₀ do początku O₁ wyrażony w układzie O x₀ y₀ z₀. W macierzy H występują również  takie wielkości jak skala i perspektywa, które  w naszym ćwiczeniu zostały pominięte. Powyższą macierz) nazwano przekształceniem jednorodnym

W naszym ćwiczeniu zdefiniowaliśmy następujące przekształcenia jednorodne:

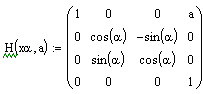
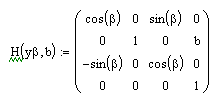
a) W dalszej części naszego ćwiczenia dokonujemy obrotu i przesunięcia (lub przesunięcia i obrotu) układu 0₁x₁y₁z₁ względem układu 0₀x₀y₀z₀ zgodnie z przekształceniem Hy. W kolejnej fazie przy pokrywających się układach 0₁x₁y₁z₁ i 0₂x₂y₂z₂ dokonujemy obrotu i przesunięcia układu 0₂x₂y₂z₂ względem 0₁x₁y₁z zgodnie z przekształceniem Hx .W każdym przypadku układ, względem, którego odbywa się obrót, nazywa się układem bieżącym.

Macierz H_1,0a opisuje obrót i przesunięcie (lub przesunięcie i obrót) między układami współrzędnych 0₀x₀y₀z₀ i 0₁x₁y₁z₁, natomiast macierz H_2,1a opisuje obrót i przesunięcie (lub przesunięcie i obrót) między układami 0₁x₁y₁z₁ i 0₂x₂y₂z₂.

Powyższe równanie jest prawem składania przekształceń jednorodnych.

Obliczone współrzędne wektorów z powyższych równań.

W celu sprawdzenia otrzymanych wyników musimy zastosować następujące obliczenia:

W obu przypadkach dokonujemy obrotu i przesunięcia wektora.

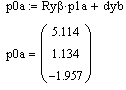
Jednakowa wartość owych wektorów potwierdza poprawność naszych wyliczeń.

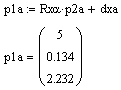
b) Kolejna część naszego ćwiczenia laboratoryjnego była podobna do poprzedniego ćwiczenia z tylko tym wyjątkiem, że dochodzi nam dodatkowy obrót i przesunięcie (lub przesunięcia i obrotu) układu 0₃x₃y₃z₃ względem 0₂x₂y₂z₂ zgodnie z przekształceniem Hz.

c) W ostatniej części naszego ćwiczenia robimy to samo co w podpunktach a) oraz b) z tą różnicą że dokonujemy obrotu wokół ustalonego układu, a nie bieżącego.

3. Wnioski

Przeprowadzone przez nas obliczenia pozwoliły nam zapoznać się z aparatem matematycznym, jaki jest wykorzystywany w robotyce, oraz poznać podstawowe funkcje oprogramowania, inżynieryjskiego jakim jest MATHCAD.

Na podstawie przeprowadzonych obliczeń, oraz wiedzy teoretycznej, wiemy, że

tego rodzaju przekształcenia stosowane są w robotyce do obliczania zadań prostych i odwrotnych manipulatorów robotów.

Zadanie proste polega na obliczeniu na podstawie zmiennych kinematycznych (czyli obrotów i wysuwów odpowiednich członów robota) położenia końcówki manipulatora (lub innego jego punktu) w globalnym (zewnętrznym) układzie współrzędnych.
Zadanie odwrotne jest trudniejsze i obejmuje wyliczenie ustawień kątów i wysuwów na podstawie zadanego położenia końcówki.

---