Write(plik,' ',X[i]:13);

end;

Writeln(plik);

licz:=0;

repeat

bl:=0;

licz:=licz+1;

for i:=1 to n do begin

s1:=0; s2:=0; s3:=0;

for j:=1 to n do

s1:=s1+Sqr(F(j,X));

for j:=1 to n do

s2:=s2+F(j,X)*W(j,i,X);

for l:=1 to n do begin

s4:=0;

for j:=1 to n do

s4:=s4+F(j,X)*W(j,l,X);

s3:=s3+Sqr(s4);

end;

sp:=0.5*s1*s2/s3;

if Abs(sp)>bl then bl:=Abs(sp);

X[i]:=X[i]-sp;

end;

until (bl<eps) or (licz=iter);

Writeln(plik);

Writeln(plik,'Liczba wykonanych iteracji: ',licz:3);

Writeln(plik);

Writeln(plik,'Rozwiązanie układu równań:');

Write(plik,' '); k:=0;

for i:=1 to n do begin

k:=k+1;

if k=5 then begin

k:=0; Writeln(plik);

Write(plik,' ');

end;

Write(plik,' ',X[i]:16);

end;

Writeln(plik); Writeln(plik);

Writeln(plik,'Residua równań:');

Write(plik,' '); k:=0;

for i:=1 to n do begin

k:=k+1;

if k=5 then begin

k:=0; Writeln(plik);

Write(plik,' ');

end;

Write(plik,' ',F(i,X):13);

end;

Writeln(plik); CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(Edit1.Text);

end;

. . . . . . . . . . . . . . . . . . . . . .

Program 3.6 jest zmodyfikowanym programem 3.5, w którym algorytm rozwiązywania układu równań nieliniowych metodą Newtona został zastąpiony algo-rytmem wynikającym z zastosowania metody najszybszego spadku. Przy wykorzystaniu programu 3.6 uzyskano następujące rozwiązanie układu (3.41) dla przybliżenia początkowego

dla którego metoda Newtona jest rozbieżna:

PROGRAM 3.6.

Rozwiązywanie układu równań nieliniowych.

Metoda najszybszego spadku.

Liczba równań układu - n = 3

Zadana liczba iteracji - iter = 80

Zadana dokładność obliczeń - eps = 1.0000E-0009

Przybliżenie początkowe:

-5.0000E+0000 -2.0000E+0000 3.0000E+0000

Liczba wykonanych iteracji: 59

Rozwiązanie układu równań:

-7.8519693E-0001 4.9661139E-0001 3.6992283E-0001

Residua równań:

-3.3782E-0009 -8.1710E-0010 1.3507E-0010

ĆWICZENIA

3.1. Stosując metodę iteracji prostej obliczyć rzeczywiste pierwiastki równań:

a)

b)

z dokładnością

3.2. Stosując metody: Newtona i połowienia obliczyć z dokładnością
pierwiastek dodatni równania

Porównać liczby iteracji dla obu tych metod.

3.3. Znaleźć pierwiastek równania

metodą stycznych i metodą siecznych. Dla każdej metody wyznaczyć liczbę kroków iteracyjnych, niezbędnych do uzyskania pierwiastka równania z zadaną dokładnością
w przedziale

3.4. Napisać program przeznaczony do rozwiązywania równania

metodą stycznych i metodą regula falsi. Dla każdej metody należy ponadto drukować liczbę kroków iteracyjnych, potrzebnych do uzyskania pierwiastka z dokładnością ε.

3.5. Znaleźć przybliżone rozwiązanie dodatnie układu równań nieliniowych:

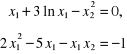
klasyczną metodą Newtona, przyjmując jako przybliżenie początkowe wektor

3.6. Metodą najszybszego spadku obliczyć pierwiastki układu równań:

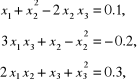
wyznaczające punkt w sąsiedztwie początku układu współrzędnych

3.7. Korzystając z metod: Newtona i najszybszego spadku wyznaczyć przybliżone rozwiązanie układu równań nieliniowych:

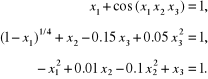
156 3. Równania nieliniowe

Ćwiczenia 157

---