Niech popyt D_t oraz podaż S_t pewnego dobra w okresie t opisują dwie relacje:

,

,

,

gdzie: P_t - cena rynkowa dobra w okresie t,

M_t - dochody nabywców w okresie t.

1. Dokonać linearyzacji obydwu równań,

2. Zapisać postać strukturalną modelu,

3. Określić typ zmiennych modelu,

4. Określić klasę modelu ze względu na powiązania pomiędzy zmiennymi objaśnianymi,

5. Czy model jest identyfikowalny?

6. Wybrać metodę estymacji parametrów modelu.

1. Trzy równania modelu, to relacje nieliniowe. Logarytm obydwu stron każdego równania, to równoważna postać liniowa względem parametrów strukturalnych:

,

,

.

Podstawiając:
,
,
oraz
, otrzymujemy:

,

,

.

II.

,

,

.

W zapisie rachunku macierzy:

+

+
=
,

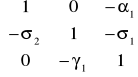
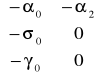
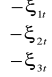
gdzie:

=
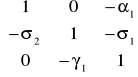
, A =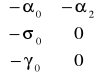
, Y =
, X =
,
=
,

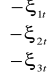
stąd
.

1. Zmienne macierzy Y , to zmienne łącznie współzależne, zmienne macierzy X , to zmienne z góry ustalone.

2. Macierz
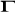
   nie jest ani macierzą diagonalna ani trójkątną, zatem jest to model o równaniach współzależnych.

3. Identyfikowalność modelu:

1. równanie pierwsze - w równaniu tym nie występuje zmienna Y_2t, zatem macierz parametrów strukturalnych przy zmiennej Y_2t lecz nie występujących w pozostałych równaniach modelu przyjmie postać /chodzi o równanie drugie i trzecie/:

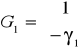
, zakładając, że oceny parametrów strukturalnych modelu różnią się istotnie od zera, to rząd macierzy G jest równy 1, rz(G) = 1, liczba równań modelu h=3, stąd nie jest spełniony warunek konieczny i dostateczny Tw. o identyfikowalności /rz(G) = h - 1/,

2. równanie drugie - w równaniu nie występuje zmienna X_t, macierz parametrów strukturalnych przy tej zmiennej w równaniu pierwszym i trzecim jest równa:

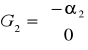
, zakładając, że parametr
różni się istotnie od zera, wówczas rząd macierzy G₂ jest równy 1, zatem także i w tym przypadku nie jest spełniony warunek konieczny i dostateczny Tw. o identyfikowalności,

3. równanie trzecie - w równaniu nie występują zmienne: Y_1t oraz X_t, macierz parametrów strukturalnych przy tych zmiennych w równaniu pierwszy i drugim jest równa:

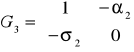
, zakładając, że parametr
różni się istotnie od zera, wówczas rząd macierzy G₃ jest równy 2, co oznacza, iż trzecie równanie modelu jest identyfikowalne, liczba zmiennych nie występujących w tym równaniu q=2, jest równa h - 1, a to oznacza, że równanie jest identyfikowalne jednoznacznie.

VI. Jedynym możliwym wyborem metody estymacji jest 2MNK.