9. Normalność składnika losowego.

Podstawową własnością rozkładu normalnego jest symetria oraz mezokurtyczność. Asymetria rozkładu wynika z nierównomierności prawostronnego i lewostronnego rozproszenia, co oznacza, że wartości liczbowe średniej, mediany i dominanty nie pokrywają się.

Standardową miarą asymetrii rozkładu jest współczynnik skośności, określany także mianem współczynnika asymetrii:

;

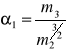
gdzie:
, k=2,3,4,…

Dodatnia wartość
wskazuje na prawostronną asymetrię, natomiast wartość ujemna
na asymetrię lewostronną.

Kurtoza rozkładu wyraża się albo tym, że gęstość rozkładu obserwacji w pobliżu średniej jest większa niż dla rozkładu normalnego, albo tym, że gęstość rozkładu w pobliżu średniej jest mniejsza iż dla rozkładu normalnego. W pierwszym przypadku rozkład cechuje tzw. smukłość, drugi przypadek określamy mianem spłaszczenia rozkładu. Miarą nasilenia kurtozy jest współczynnik kurtozy:

.

Dla rozkładu normalnego, współczynnik kurtozy jest równy
, stąd w praktyce, współczynnik kurtozy definiowany jest jako odchylenie od standardu, czyli

Do weryfikacji hipotez
- rozkład zgodny z rozkładem normalnym} wobec hipotezy alternatywnej
nie ma rozkładu normalnego} korzystamy ze statystyki Jarque'a-Bera
:

Weryfikacja zgodności rozkładu składnika losowego z rozkładem normalnym prowadzona jest na podstawie reszt modelu, stąd:

, j=1,2,3…,

statystykę Jarque'a-Bera można zapisać w postaci równoważnej:

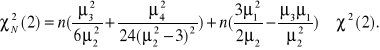
Z tablic testu
dla określonego poziomu ufności
oraz n-2 stopni swobody odczytujemy wartość krytyczną
. Jeśli
, to nie ma powodów do odrzucenia hipotezy
, składnik losowy jest zgodny z rozkładem normalnym, jeśli natomiast
, należy odrzucić hipotezę
i przyjąć hipotezę alternatywną
.

Zweryfikowany zbiór własności elementów struktury modelu dotyczył zarówno zmiennych modelu ale także i to w dużej części składnika losowego. Proces weryfikacji powinien zostać uzupełniony o testy istotności łącznego wpływu zmiennych objaśniających, test na dołączanie i usuwanie zmiennych, weryfikację poprawności założenia o postaci analitycznej oraz testy stabilności struktury modelu weryfikowanej w kontekście stałości oszacowanych parametrów strukturalnych czasie.

10. Istotność łącznego wpływu zmiennych objaśniających.

Definiujemy hipotezę
wobec hipotezy alternatywnej
istnieje takie i, że
. Sprawdzianem hipotezy
jest statystyka:

.

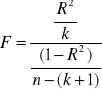
Z tablic rozkładu statystyki F przy określonym poziomie istotności
oraz parametrach rozkładu
, odczytujemy wartość krytyczną statystyki
. Jeśli
, to ma podstaw do odrzucenia hipotezy
, jeśli natomiast
, odrzucamy hipotezę
na rzecz hipotezy alternatywnej
.

11. Test na dołączenie i usuwanie zmiennych.

Budując model ekonometryczny zadajemy sobie pytanie, na ile włączenie dodatkowej zmiennej poprawia dokładność opisu zmian zmiennej objaśnianej. Miarą zgodności czy też dopasowania modelu do danych empirycznych jest współczynnik
. Stąd pytanie, czy uwzględnienie nowej zmiennej w modelu poprawi istotnie stopień dopasowania mierzony współczynnikiem
?.

Niech
, ponadto załóżmy, że stopień dopasowania modelu do danych empirycznych mierzy
/współczynnik determinacji modelu pierwotnego, przed dołączeniem dodatkowej zmiennej objaśnianej/.

Pierwotny zbiór zmiennych objaśniających uzupełnimy o zmienne {
, tzn. ,
miarę dopasowania modelu o tak uzupełniony zbiór zmiennych oznaczmy jako
.

Chcemy zatem zweryfikować hipotezę
wobec hipotezy alternatywnej
istnieje takie j, że k+1
oraz
. Sprawdzianem hipotezy
jest statystyka F:

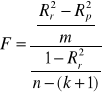
, gdzie m liczba dołączonych zmiennych.

Statystyka F ma rozkład Fishera-Snedecora o parametrach rozkładu
. Z tablic rozkładu statystyki dla poziomu istotności
odczytujemy wartość statystyki
. Jeśli
nie ma podstaw do odrzucenia hipotezy
, jeśli natomiast
, odrzucamy hipotezę
na rzecz hipotezy alternatywnej
, co oznacza, że dołączenie nowej zmiennej powoduje istotne zwiększenia stopnia dopasowania modelu.

12. Poprawność założenia o postaci analitycznej modelu.

Najprostszym rozwiązaniem wątpliwości z tym związanych jest sprawdzenie, czy kwadraty wartości teoretycznych zmiennej objaśnianej nie stanowią „pominiętej zmiennej” w budowanym modelu. Sprawdzamy zatem, czy włączenie dodatkowej zmiennej powoduje istotny wzrost współczynnika determinacji
.

Idea weryfikacji podana została przez Ramseya. Sprawdzian testu ma dwie wersje,
o rozkładzie
oraz wersję
o rozkładzie Fishera-Snedecora
.

Weryfikujemy hipotezę
błąd w założeniu o postaci analitycznej} wobec hipotezy alternatywnej
poprawna postać analityczna}. Z tablic rozkładu
bądź rozkładu statystyki F odczytujemy wartości krytyczne obydwu statystyk, statystykę
weryfikujemy identycznie jak w teście Godfreya.

13. Stabilność parametrów strukturalnych modelu.

Po oszacowaniu parametrów strukturalnych modelu, ciekawe staje się pytanie, czy oszacowane parametry nie zmieniają się w czasie? To ważne pytanie, bowiem od stałości parametrów zależy wiarygodność konstruowanych prognoz zmian zmiennej objaśnianej w przyszłości.

W 1960 r. Chow podał sprawdzian stabilności parametrów modelu. Należy dokonać podziału próby na dwa podzbiory
oraz
takie, że
.

Zatem model możemy zapisać:

,

Weryfikujemy hipotezę
wobec hipotezy alternatywnej
. Sprawdzianem hipotezy
jest statystyka
dla dużych prób i statystyka
dla prób małych.

,

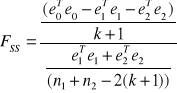
gdzie:
- wektor reszt modelu szacowanego MNK na podstawie całej próby n,

- wektor reszt modelu szacowanego MNK na podstawie próby n₁,

- wektor reszt modelu szacowanego MNK na podstawie próby n₂.

Przy założeniu, że wariancje składnika losowego w obydwu „podpróbach” są sobie równe, statystyka
ma rozkład Fishera-Snedecora o (
stopniach swobody a statystyka:

, ma rozkład
.

Z tablic rozkładu statystyk F oraz
odczytujemy wartości krytyczne. Jeśli statystyki obliczone są mniejsze lub równe wartościom krytycznym statystyk, to nie ma powodów by przyjąć hipotezę
, w przeciwnym przypadku uznajemy hipotezę alternatywną
, co oznacza, że parametry strukturalne nie są stabilne w czasie.