W licznych przypadkach dla opisu prawidłowości ekonomicznych, model jednorównaniowy nie jest wystarczający, w takich przypadkach jest wówczas zbiorem kilku równań, które są obrazem powiązań nie tylko pomiędzy zmiennymi objaśniającymi i objaśnianymi, uwzględniają także relacje pomiędzy zmiennymi objaśnianymi.
Niech ![]()
oraz ![]()
,
gdzie: Yit - i-ta zmienna objaśniana, ponieważ zmienne objaśniane w pozostałych równaniach modelu wielorównaniowego mogą być zmiennymi objaśniającymi, zatem przyjęto nazywać je zmiennymi łącznie współzależnymi,
Xjt - j-ta zmienna objaśniająca, ten zbiór zmiennych przyjęto określać mianem zmiennych z góry ustalonych.
Ponadto załóżmy, że wszystkie równania modelu są liniowe względem parametrów strukturalnych, wówczas model możemy zapisać jako zbiór h równań postaci:
![]()
,
(1.1) ![]()
,
……………………………………………..
![]()
.
Jeśli oznaczymy:
![]()
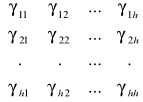
, A = 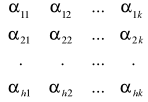
, Y = ![]()
, X = ![]()
, ![]()
= ![]()
,
to układ (1.1) zapiszemy jako ![]()
= 0, jest to postać strukturalna modelu.
Wzajemne relacje pomiędzy zmiennymi łącznie współzależnymi, określają rodzaj modelu ekonometrycznego. Przyjmując bowiem jako kryterium rodzaju, właściwości powiązań pomiędzy tą klasą zmiennych modelu, wyróżniono modele: proste, rekurencyjne i modele o równaniach współzależnych.
Z klasą modelu związana jest postać macierzy ![]()
, jeśli jest to macierz diagonalna, wówczas zdefiniowany model jest modelem prostym, tzw. macierz trójkątna określa model rekurencyjny, jeśli natomiast macierz ![]()
, nie jest ani macierzą diagonalną ani trójkątną, to model jest zbiorem relacji o równaniach współzależnych.
To rozróżnienie jest szczególnie ważne, bowiem niesie ważne implikacje dotyczące estymacji parametrów strukturalnych modelu. W równaniach modeli o równaniach współzależnych, wśród zmiennych objaśniających występują zmienne, które w innych równaniach modelu są zmiennymi objaśniającymi a jednocześnie zależą od składnika losowego![]()
. Z założeń kmnk wynika jednoznacznie, iż niedopuszczalne są zależności pomiędzy zmiennymi objaśniającymi modelu a składnikiem losowym. Zależności takie przekreślają możliwość stosowania tej metody estymacji w przypadku modeli o równaniach współzależnych. Ten wniosek nie dotyczy jednakże pewnego przypadku szczególnego, który wymaga osobnego omówienia.
Załóżmy, że istnieje macierz odwrotna macierzy ![]()
, jeśli postać strukturalną modelu pomnożymy lewostronnie stronami przez ![]()
wówczas otrzymamy:
![]()
(![]()
)= 0,
![]()
,
![]()
,
![]()
,
![]()
,
gdzie: ![]()
, ![]()
.
Równanie ![]()
, równoważne postaci strukturalnej modelu wielorównaniowego, określana jest w ekonometrii jako postać zredukowana. Jej charakterystyczną własnością jest to, iż z punktu widzenia powiązań pomiędzy zmiennymi łącznie współzależnymi stanowi model prosty. W modelach tej klasy nie występują zależności pomiędzy zmiennymi łącznie współzależnymi i składnikami losowymi, które przekreślają możliwość stosowania kmnk. Oznacza to, że w takim przypadku bez ograniczeń można oszacować parametry strukturalne ![]()
.
W tym miejscu należy zastanowić się nad możliwością wykorzystania informacji o oszacowanych parametrach strukturalnych ![]()
do wyznaczenia elementów macierzy A oraz ![]()
. Gdyby było to możliwe, to oznaczałoby iż problem oszacowania parametrów strukturalnych postaci strukturalnej modelu zostałby rozwiązany.
Tak sformułowane zadanie wymaga odpowiedzi na pytanie o istnienie rozwiązań równania macierzowego ![]()
. Nie chodzi tu o dowolne rozwiązanie lecz takie, które ma jedną istotną własność, jest jedynym i jednoznacznym rozwiązaniem tego równania.
Odpowiedź na sformułowane pytanie o tak szczególne własności rozwiązania równania wiąże się z identyfikowalnością równań modelu. Jest to taka własność strukturalna równań, która pozwala oszacować jednoznaczne wartości parametrów strukturalnych modelu postaci strukturalnej.
Metoda szacowania parametrów strukturalnych modelu, wykorzystująca postać zredukowaną do oceny parametrów postaci strukturalnej określana jest w ekonometrii mianem „pośredniej metody najmniejszych kwadratów”. Z oczywistych więc względów warto sprawdzić możliwość jaką daje ta metoda estymacji, wymaga to jednak definicji efektywnych instrumentów dających jednoznaczną odpowiedź na pytanie o identyfikowalność poszczególnych równań modelu o równaniach współzależnych. Odpowiedź na tak sformułowane pytanie daje teza następującego twierdzenia:
Tw 1. Warunkiem koniecznym i dostatecznym na to, by dowolne równanie modelu o h równaniach współzależnych było identyfikowalne jest, by macierz utworzona z parametrów strukturalnych w pozostałych równaniach modelu przy zmiennych nie występujących w równaniu którego identyfikowalność analizujemy była rzędu h - 1.
Niech q oznacza liczbę tych zmiennych modelu, które nie występują w równaniu którego identyfikowalność rozważamy. Zachodzić mogą trzy przypadki:
q = h - 1; 2. q > h - 1; 3. q < h - 1.
Jeżeli q = h - 1 i spełniona jest teza twierdzenia Tw. 1, to równanie modelu jest jednoznacznie identyfikowalne,
Jeżeli q > h - 1 i spełniona jest teza twierdzenia Tw. 1, to równanie modelu jest niejednoznacznie identyfikowalne,
Jeżeli q < h - 1, to równanie modelu jest nieidentyfikowalne.
Jeżeli wszystkie równania modelu są identyfikowalne, to model jest identyfikowalny. Jeśli model takiej własności nie ma, nie ma tym samym możliwości stosowania pośredniej metody najmniejszych kwadratów i oznacza to konieczność opisu takiej procedury, która rozwiązywałaby problem szacowania parametrów strukturalnych postaci strukturalnej.
Niech:
![]()
, gdzie zmienna Y1t objaśniana jest przez wszystkie bądź niektóre zmienne Ylt oraz zmienne z góry ustalone Xjt /być może wszystkie, bądź tylko niektóre/, procedurę szacowania parametrów ![]()
podzielmy na dwa etapy:
Kmnk szacujemy parametry strukturalne relacji:
![]()
, gdzie ![]()
oraz ![]()
i ![]()
,
Teoretyczne wartości zmiennych łącznie współzależnych
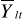
podstawiamy do równania objaśniającego zmienną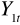
, otrzymamy:
![]()
.
Parametry ![]()
szacujemy kmnk.
Oszacujmy parametry strukturalne równania „z” modelu wielorównaniowego, postać macierzowa równania:
![]()
,
gdzie: Y(z) - zmienna łącznie współzależna, objaśniana w równaniu (z),
Y(z)i - macierz K zmiennych łącznie współzależnych będących zmiennymi objaśniającymi w równaniu (z),
![]()
- macierz parametrów strukturalnych postaci strukturalnej modelu przy zmiennych łącznie współzależnych,
X(z)j - macierz F zmiennych z góry ustalonych będących zmiennymi objaśniającymi w równaniu (z),
![]()
- macierz parametrów strukturalnych postaci strukturalnej modelu przy zmiennych z góry ustalonych,
![]()
- składnik losowy równania (z).
Postać zredukowana równania (z): ![]()
Parametry strukturalne ![]()
szacujemy kmnk, tzn. ![]()
=![]()
, wartości teoretyczne ![]()
wyznaczymy z relacji ![]()
= ![]()
, stąd ![]()
=X![]()
. Wyznaczając wartości teoretyczne ![]()
, możemy tym samym zapisać relację pomiędzy wartościami teoretycznymi, empirycznymi i resztami: ![]()
= ![]()
(z)i + ![]()
.
Stąd:
![]()
![]()
i następnie ![]()
.
Oznaczmy macierz Z(z) = ![]()
oraz 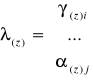
,
wówczas : ![]()
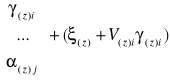
,
ostatecznie ![]()
.
Parametry ![]()
oszacowano kmnk, tzn. ![]()
,
Stąd 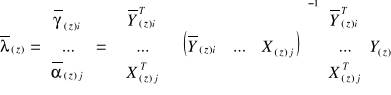
, i dalej
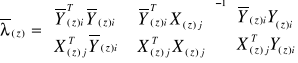
= 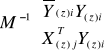
Oszacowanie parametrów ![]()
jest możliwe jeśli macierz M nie jest macierzą osobliwą.
Otrzymany wynik można zapisać w postaci równoważnej:
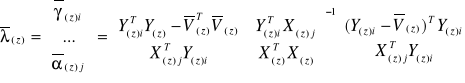
,
gdzie: ![]()
.
Macierz wariancji i kowariancji estymatora ![]()
jest wyznaczana z zależności 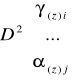
Stąd 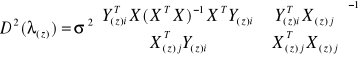
, gdzie aproksymantą wariancji składnika losowego ![]()
jest wariancja resztowa Se2, wyznaczona wg. formuły:
![]()
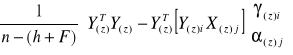
.
Wyszukiwarka
Podobne podstrony:
Fuzje i przejęcia - wykłady, WZR UG ZARZĄDZANIE - ZMP I STOPIEŃ, V SEMESTR (zimowy) 2014-2015, FUZJE
Ekonometria wyklad 3.2, Ekonomia UG, 2, Ekonometria
Ekonometria wyklad 3.4, Ekonomia UG, 2, Ekonometria
Ekonometria wyklad 1, Ekonomia UG, 2, Ekonometria
Geografia turystyczna wykłady na UG
Geografia turystyczna, wykłady na UG
Finanse - wykład, FiR UG LSN, 5 semestr, Finanse samorządu terytorialnego, Finanse samorządu terytor
Zarządzanie Jakością wykłady, ZARZĄDZANIE - UG, SEMESTR 3, Zarządzanie jakością
Ekonometria wyklad 5, Ekonomia UG, 2, Ekonometria
Podstawy zarządzania wykłady, ZARZĄDZANIE - UG, SEMESTR 2, Podstawy zarządzania
wykład 1-3, wzr UG, OWI
Ekonometria wyklad 2, Ekonomia UG, 2, Ekonometria
Ekonometria wyklad 3.1, Ekonomia UG, 2, Ekonometria
PRODUKTY UBEZEPIECZENIOWE - PIERWSZY WYKŁAD, WZR UG ZARZĄDZANIE - ZMP I STOPIEŃ, V SEMESTR (zimowy)
Ekonometria wyklady 3.3, Ekonomia UG, 2, Ekonometria
Podstawy Zarzadzania - M.Czerska - WYKLADY, ZARZĄDZANIE - UG, SEMESTR 2, Podstawy zarządzania
więcej podobnych podstron