Wykład 2. Klasyczna metoda najmniejszych kwadratów.

Załóżmy, że zmienne
stanowią zbór zmiennych objaśniających zmiany zmiennej
. Oznacza to, że obydwa zbiory zmiennych wchodzą w relację
, postaci:
. Relacja
jest odwzorowaniem, któremu przypisujemy pewną szczególną własność, jest funkcją, nie jest obojętne jaką postać analityczną przyjmuje.

Zdefiniujmy kolejne, drugie założenie, zgodnie z którym, relacja
jest odwzorowaniem funkcyjnym liniowym postaci:

,

gdzie:
- zbiór zmiennych objaśniających,

- zmienna objaśniana,

- parametry strukturalne,

- składnik losowy.

Zwykle nie mamy pełnej informacji o wartościach parametrów strukturalnych
. Ich wartości numeryczne można oszacować, jednakże procedurę wnioskowania, znaną w literaturze ekonometrycznej jako proces estymacji, poprzedza przyjęcie funkcji kryterium dopasowania modelu do danych empirycznych.

Klasyczna ekonometria przyjmuje takie kryterium jest nim funkcja będącą sumą kwadratów odchyleń pomiędzy wartościami empirycznymi /zmierzonymi/ a wartościami teoretycznymi, zdefiniowanymi w (2.1).

(2.2)
.

Funkcja
osiąga minimum dla takiego zbioru oszacowań
dla którego pochodne cząstkowe funkcji
względem każdego parametru
, /gdzie:
/ przyjmują wartość zero:

.

Pochodne cząstkowe
definiują układ
równań o
niewiadomych parametrach
:

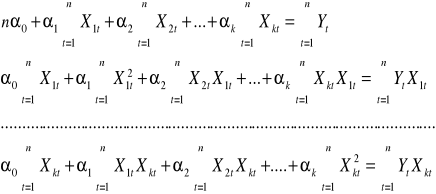
(2.3)

Układ równań (2.3) jest układem równań niejednorodnych, układ taki może mieć rozwiązanie bądź nie. Był rozwiązać układ musi być spełniony warunek sformułowany przez Kroneckera - Capelliego, zgodnie z jego treścią, rzędy macierzy głównej i uzupełnionej muszą być takie same.

Pozostaje rozstrzygnąć jednoznaczność rozwiązania, jeśli bowiem spełniony jest warunek Kroneckera - Capelliego a ponadto rzędy macierzy głównej oraz uzupełnionej są równe liczbie niewiadomych układu, wówczas rozwiązanie, jest rozwiązaniem jedynym i jednoznacznym.

Zdefiniowany układ równań, literatura ekonometryczna określa mianem układu równań normalnych. Jego rozwiązanie jeśli istnieje i jest jednoznaczne, informuje o wartościach parametrów strukturalnych modelu. Jest to jednak mimo swojej skuteczności metoda mało efektywna, głównie czasochłonna, wymagająca czasu na zdefiniowanie układu równań normalnych a następnie dyskusję dotyczącą istnienia oraz liczby rozwiązań zdefiniowanego układu.

Dużym uproszczeniem procesu wnioskowania o wartościach numerycznych parametrów strukturalnych jest zapis modelu przy użyciu pojęć rachunku macierzowego.

Oznaczmy:

- macierz zmiennych objaśnianych,

- macierz zmiennych objaśniających,

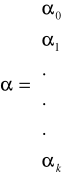
- macierz parametrów strukturalnych modelu,

- macierz składników losowych.

Model (2.1) po uwzględnieniu przyjętych powyżej oznaczeń przyjmie postać:

,

Realizacją składnika losowego są reszty modelu „
” równe:

,

gdzie „
” są ocenami parametrów strukturalnych α.

Założenia:

1. liniowa postać analityczna modelu,

2. zmienne objaśniające są wielkościami nielosowymi,

3. składnik losowy ma wartość oczekiwaną zero i stałą wariancję σ² o skończonej wartości / stałość wariancji rozumiana jest jako jej niezależność od t/,

4. realizacje zmiennych są niezależne, co sprawia, że ciąg {ξ_t} jest ciągiem niezależnych zmiennych losowych,

5. składnik losowy jest nieskorelowany ze zmiennymi objaśniającymi,

6. zmienne objaśniające nie są współliniowe.

Funkcja kryterium dopasowania modelu do danych empirycznych jest równa:

,

,

,

.

Pochodna cząstkowa
,

stąd
.

Jeśli spełnione są założenia
to macierz wariancji i kowariancji D²(
) estymatora „
” jest równa:

,

gdzie:
jest wariancją składnika losowego.

Ponieważ nie znamy składnika losowego /znane są jedynie reszt równania/ stąd σ² zastępujemy oceną
, gdzie:

.

Licznik wyrażenia jest równy
. Pierwiastek kwadratowy z
nazywamy błędem standardowym.

Zgodność modelu z „rzeczywistością” mierzy współczynnik determinacji
, jest ilorazem odchyleń wartości teoretycznych zmiennej objaśnianej
od wartości średniej tej zmiennej do odchyleń wartości empirycznych zmiennej objaśnianej od wartości średniej zmiennej:

.

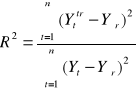
Współczynnik determinacji przyjmuje wartości z przedziału
. Wartość tego współczynnika określa jaką część zmienności zmiennej objaśnianej opisuje przyjęty zbiór zmiennych objaśniających.

Miarę zgodności opisu uzupełniają błędy średnie szacunku parametrów strukturalnych. Wyznaczane są w oparciu o elementy macierzy wariancji i kowariancji estymatora
. Błędy średnie szacunku parametrów są pierwiastkami z wariancji estymatora,
.