XV Ciała i sigma-ciała zbiorów. Zbiory borelowskie. Definicja miary przeliczalnie addytywnej.

Definicja

Zakładamy, że X jest pewnym zbiorem oraz
będzie rodziną pewnych podzbiorów (
). Mówimy, że
jest
-ciałem, jeśli spełnione są w-ki:

1).

2).

3). Dla dowolnego ciągu
jeśli
dla dowolnego
, to
.

Jeśli
spełnia warunki 1, 2 , 3^'
to taką rodzinę nazywamy ciałem zbiorów.

Twierdzenie (własności
-ciała)

Załóżmy, że
jest
-ciałem. Wówczas zachodzą następujące warunki:

4).

5). dla dowolnego
i dowolnych

6). dla dowolnego ciągu nieskończonego
zbiorów należących do
,
.

7). dla dowolnego
i dowolnego

8).
.

Definicja

Załóżmy, że
jest p-nią metryczną oraz
oznacza rodzinę wszystkich otwartych podzbiorów p-ni X. Zbiorem borelowskim p-ni
nazywamy zbiory należące do najmniejszego
-ciała
zawierającego rodzinę
. Rodzinę wszystkich zbiorów borelowskich będziemy oznaczać symbolem
.

Definicja

Mówimy, że funkcja
jest przeliczalnie addytywna funkcją zbioru jeśli dla dowolnego ciągu
zbiorów należących do
i takich, że
zachodzi

.

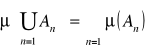
Definicja

Załóżmy, że X jest pewnym zbiorem,
jest
-ciałem. Funkcję
nazywamy miarą jeśli:

1)

2).
jest przeliczalnie addytywną funkcją zbioru.

Wówczas trójkę (
) nazywamy p-nią z miarą, elementy rodziny M zb. mierzalnymi.

---