Dr Piotr SZCZEPANKOWSKI

ZARZĄDZANIE FINANSAMI PRZEDSIĘBIORSTW

(wykład nr 6)

Temat: MIERNIKI OCENY OPŁACALNOŚCI INWESTYCJI

A. Oceniając efektywność przedsięwzięć inwestycyjnych najczęściej wykorzystuje się mierniki finansowe sklasyfikowane w dwóch grupach metod - prostych i dyskontowych.

B. Metody proste oceniają opłacalność inwestycji bazując na prognozowanych przepływach pieniężnych bez uwzględnienia zmian wartości pieniężnych w czasie. Do tych metod zalicza się:

• okres zwrotu nakładów inwestycyjnych, nazywany także okresem spłaty (Payback Period - PP),

• księgową (średnią) stopę zwrotu (Accounting (Average) Rate of Return - ARR),

• prostą stopę zysków z zainwestowanych kapitałów (Return on Investment Capital - ROIC),

• koncepcję progu rentowności (Break Even Point Approach - BEP).

C. Metody dyskontowe analizują opłacalność przedsięwzięcia inwestycyjnego opierając się na zaktualizowanych wartościach przyszłych strumieni pieniężnych możliwych do osiągnięcia z danego projektu rozwojowego. Bazują więc one na dyskontowanych przepływach pieniężnych, czyli przepływach uwzględniających zarówno czynnik zmiany wartości pieniężnych w czasie, jak i wszystkie składniki ryzyka inwestycyjnego. Do dyskontowych metod oceny opłacalności inwestycji zalicza się następujące mierniki:

• wartości obecnej netto (Net Present Value - NPV),

• wewnętrznej stopy zwrotu z inwestycji (Internal Rate of Return - IRR),

• zmodyfikowanej wewnętrznej stopy zwrotu z inwestycji (Modified Internal Rate of Return - MIRR).

• indeksu zyskowności inwestycji (Profitability Index - PI),

• zdyskontowany okres zwrotu (Discounted Payback Period - DPP).

1. Proste metody oceny opłacalności projektów inwestycyjnych

Okres zwrotu nakładów inwestycyjnych

A. Okres zwrotu nakładów inwestycyjnych (okres spłaty) oznacza czas, w jakim przewiduje się zrównanie wartości początkowego nakładu z nadwyżkami finansowymi, których uzyskania oczekuje się dzięki realizacji danego projektu. Innymi słowy jest minimalna wymagana liczba lat potrzebna do odzyskania z przyszłych wpływów środków finansowych poniesionych na przedsięwzięcie inwestycyjne.

B. Najprostszą metodą obliczania okresu zwrotu jest kumulowanie planowanych przepływów pieniężnych z wartością początkowego nakładu inwestycyjnego i sprawdzenie, kiedy suma ta wyniesie zero.

C. Jeśli okres zwrotu nakładów inwestycyjnych jest mniejszy lub równy przyjętej liczbie dopuszczalnych lat zwrotu wydatków na przedsięwzięcie, to dana inwestycja jest akceptowana do realizacji. Natomiast, gdy okres zwrotu nakładów inwestycyjnych jest większy niż ustalona graniczna liczba lat zwrotu, wówczas to przedsięwzięcie jest odrzucane jako nieefektywne. Graniczny okres, przyjęty jako dopuszczalny, jest zazwyczaj określony na podstawie dotychczasowych doświadczeń innych firm inwestujących w podobne przedsięwzięcia.

D. Omawiane metoda cechuje się licznymi wadami:

• nie bierze się w niej pod uwagę całego okresu funkcjonowania projektu,

• pomija się w ocenie strumienie efektów wykraczające poza okres zwrotu nakładów,

• metoda ta nie uwzględnia zmiany wartości pieniądza w czasie, pomija się tutaj zatem wpływ czasu na wartość efektów wyrażonych w pieniądzu,

• okres zwrotu nie daje odpowiedzi, czy projektowane przedsięwzięcie zapewnia zyskowność, jaką można by osiągnąć w przypadku innej formy lokaty kapitału (np. na rachunku inwestycyjnym w banku).

E. Zaletą kryterium okresu zwrotu jest prostota obliczeń i łatwość interpretacji wyników. Kryterium to preferuje inwestycje o szybkim okresie zwrotu i z tego powodu jest przydatne w warunkach niepewności i ryzyka, będącego wynikiem walki konkurencyjnej na rynku oraz szybkiego postępu naukowo-technicznego. Okres zwrotu jest preferowany w sytuacjach, w których są potrzebne szybkie oceny i decyzje, nie powinien być natomiast stosowany do oceny projektów charakteryzujących się długim horyzontem czasowych realizacji.

PRZYKŁAD:

Przedsiębiorstwo LM rozważa podjęcie realizacji jednego z dwóch możliwych przedsięwzięć inwestycyjnych, wymagających takiej samej wartości zaangażowanego kapitału, dla których przygotowano następujące preliminarze finansowe przyszłych oczekiwanych z nich korzyści (dane w tys. zł):

OKRES	PLANOWANE PRZEPŁYWY PIENIĘŻNE NETTO
		PROJEKT L	PROJEKT M
0	(1.000)	(1.000)
1	500	(500)
2	400	100
3	300	300
4	100	500
5	(100)	1.000

Ustal okres zwrotu nakładów inwestycyjnych poniesionych na projekt L lub na projekt M.

ROZWIĄZANIE:

Najłatwiej wyznaczymy okres zwrotu poprzez sumowanie przepływów pieniężnych od okresu „0” do okresu „n” i sprawdzanie, kiedy suma ta wyniesie zero.

I tak:

Okres zwrotu dla projektu L (PP) = ponad 2 lata

Okres zwrotu dla projektu M (PP) = prawie 5 lat

Wynika z tego, że bardziej opłacalnym jest projekt L, gdyż charakteryzuje się krótszym okresem spłaty (zwrotu) poniesionych na jego sfinansowanie nakładów kapitałowych.

Księgowa (średnia) stopa zwrotu (ARR)

A. Księgowa stopa zwrotu (ARR) jest to przeciętna wartość okresowej dochodowości możliwej do osiągnięcia z inwestycji w zakładanym czasie jej eksploatacji. Oblicza się ją jako wartość średniej arytmetycznej z przyszłych strumieni pieniężnych generowanych z inwestycji w relacji do wartości początkowego nakładu inwestycyjnego. Prezentuje to poniższy wzór:

ARR =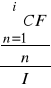
x 100%

gdzie:

ARR - księgowa stopa zwrotu,

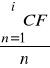
- przeciętna z jednego okresu wartość przyszłych przepływów pieniężnych netto możliwych do osiągnięcia z inwestycji,

I - wartość początkowego nakładu inwestycyjnego.

B. Przy wyborze lepszego wariantu inwestycji należy się kierować maksymalizacją wskaźnika ARR. ARR jest wygodnym narzędziem rozpatrywania projektów. Przede wszystkim cechuje się dużą prostotą i łatwością obliczeń.

C. Do wad miernika ARR możemy zaliczyć:

• nie uwzględnianie czynnika czasu w analizie zmian wartości pieniężnych w okresie wykorzystywania inwestycji,

• nie wprowadzenie jakiejkolwiek obiektywnej reguły decyzyjnej,

• oparcie analizy atrakcyjności przedsięwzięcia od średniej wartości przyszłych korzyści, co oznacza przykładowo, że ujemne przepływy pieniężne uzyskiwane w pierwszych latach eksploatacji inwestycji mogą być pokryte wysokimi dodatnimi przepływami z późniejszych lat wykorzystania projektu.

Z listy wad wynika, że miernik ARR może być, podobnie jak okres zwrotu, stosowany jako pomocnicze narzędzie wyboru przedsięwzięć na wstępnym etapie rozpatrywania alternatywnych projektów inwestycyjnych.

PRZYKŁAD:

Wyznacz księgową stopę zwrotu (ARR) dla projektów L i M rozważanych przez przedsiębiorstwo LM, i opisanych w treści poprzedniego przykładu.

ROZWIĄZANIE:

Dla projektu L średnia okresowa wartość przepływów pieniężnych wyniesie:

=
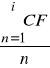
= 240 tys. zł

Tak więc ARR dla projektu L jest równe:

ARR = (240 tys. zł / 1.000 tys. zł) x 100% = 24%

ARR dla projektu M postaraj się obliczyć sam.

Stopa zwrotu z zaangażowanych kapitałów (ROIC)

A. Stopa zwrotu z zaangażowanych w inwestycję kapitałów stanowi relację średniej wartości zysków operacyjnych po opodatkowaniu uzyskiwanych z przedsięwzięcia w zakładanym okresie jego eksploatacji i wartości całkowitych nakładów inwestycyjnych (nakładów kapitałowych) poniesionych na sfinansowanie tego projektu.

B. Stopę zwrotu z zaangażowanych kapitałów najczęściej ustala się według następującej formuły:

ROIC =
x 100%

gdzie:

NOPAT - średni roczny poziom zysku operacyjnego po opodatkowaniu możliwy do osiągnięcia z danej inwestycji,

IC - wartość początkowego nakładu inwestycyjnego (wartość ogółem kapitału zaangażowanego w przedsięwzięcie).

C. Posługując się miernikiem ROIC wybiera się te projekty inwestycyjne, które przy tych samych nakładach kapitałowych przynoszą wyższą okresową stopę zwrotu.

PRZYKŁAD:

Firma KLON chce zrealizować jedną z dwóch możliwych i dostępnych inwestycji. Zarówno projekt A, jak i projekt B wymagają zaangażowania 2.500 tys. zł. Oceniono, że projekty te mogą w kolejnych pięciu latach wygenerować następujące zyski operacyjne po opodatkowaniu (NOPAT):

ROK	PROJEKT A	PROJEKT B
1	300.000 zł	500.000 zł
2	400.000 zł	300.000 zł
3	500.000 zł	100.000 zł
4	600.000 zł	50.000 zł
5	700.000 zł	- 100.000 zł

Firma oczekuje średnio w roku co najmniej 12% stopy zwrotu od zaangażowanych kapitałów. Posługując się kryterium ROIC wybierz bardziej efektywny projekt inwestycyjny.

ROZWIĄZANIE:

Dane:

Wartość zaangażowanego kapitału na jeden projekt = 2.500 tys. zł

Średni roczny poziom zysku operacyjnego po opodatkowaniu (NOPAT) projektu A = 500 tys. zł

Średni roczny poziom zysku operacyjnego po opodatkowaniu (NOPAT) projektu B = 850 tys. zł

Oczekiwana stopa zwrotu = 12% rocznie

ROIC (projekt A) = (500.000 zł / 2.500.000 zł) x 100% = 20%

ROIC (projekt B) = (850.000 zł / 2.500.000 zł) x 100% = 34%

Oba rozważane projekty inwestycyjne są efektywne dla przedsiębiorstwa, bowiem mogą przynieść stopę zwrotu od zaangażowanych kapitałów wyższą od oczekiwanej stopy zwrotu. Jednakże projekt B charakteryzuje się większym miernikiem ROIC i to on powinien być zaakceptowany do realizacji.

2. Metody dyskontowe oceny opłacalności przedsięwzięć inwestycyjnych

Wartość obecna netto (NPV)

A. Metoda wartości obecnej netto (NPV) polega na porównaniu nakładów przewidywanych na realizację inwestycji z sumy spodziewanych nadwyżek pieniężnych możliwych do osiągnięcia z projektowanego przedsięwzięcia w kolejnych okresach jego eksploatacji, ale po uprzednim sprowadzeniu ich przyszłej wartości do aktualnego poziomu (zdyskontowania) z uwzględnieniem kosztu zaangażowanego kapitału (wymaganej stopy zwrotu).

B. Wartość obecną netto (nazywaną także wartością bieżącą netto lub wartością zaktualizowaną netto) definiuje się zatem jako wartość różnicy między sumą zdyskontowanych kosztem kapitału prognozowanych przepływów pieniężnych możliwych do osiągnięcia w przyszłych okresach eksploatacji inwestycji i wartości początkowej poniesionego nakładu inwestycyjnego.

C. Kryterium NPV może być również określane jako wartość otrzymana przez zdyskontowanie, oddzielnie dla każdego okresu prognozy, różnicy między wpływami i wydatkami pieniężnymi osiąganymi z inwestycji przez cały czas eksploatacji przedsięwzięcia, przy stałym poziomie oczekiwanej stopy zwrotu (stopy dyskontowej). Różnica ta jest dyskontowana na moment, w którym przewidywane jest rozpoczęcie budowy obiektu lub początek inwestycji.

D. Metoda NPV opiera się na następujących zasadach:

• skalkulowane na poszczególne przyszłe lata eksploatacji inwestycji przepływy pieniężne sprowadza się do aktualnej ich wartości za pomocą wyznaczonej stopy dyskontowej,

• wielkość stopy dyskontowej jest związana z wysokością stopy zwrotu reprezentującej oczekiwaną minimalną stopę zyskowności kapitału, który ma być zaangażowany przy realizacji danego projektu (najczęściej jest to stopa średnio ważonego kosztu kapitału - WACC),

• zdyskontowane kwoty przepływów pieniężnych, których osiągnięcie przewidywano na poszczególne lata, sumuje się oraz porównuje ich łączną wartość z wielkością nakładu inwestycyjnego, ustalając różnicę,

• za korzystne uważa się wszystkie te projekty, przy których kwota zdyskontowanych przepływów pieniężnych pokrywa co najmniej niezbędne nakłady inwestycyjne (NPV musi być wtedy dodatnie lub przynajmniej równe zero),

• warianty projektów inwestycyjnych, przy których preliminowane przepływy pieniężne (po ich zdyskontowaniu) nie zapewniają pełnego pokrycia początkowych nakładów inwestycyjnych (NPV ujemne), należy odrzucić jako nierentowne, bowiem nie zapewniają one postulowanej zyskowności kapitału, który trzeba zaangażować w realizację danego wariantu projektu.

E. Wartość obecną netto (NPV) wylicza się na podstawie następującej formuły:

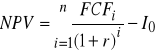
lub w wersji formuły rozszerzonej:

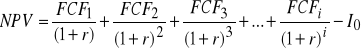
gdzie:

Io - wartość początkowego nakładu inwestycyjnego,

r - oczekiwana, stała w każdym okresie zakładanej eksploatacji inwestycji stopa zwrotu z zaangażowanych w przedsięwzięcie funduszy, najczęściej związana z szacowanym kosztem kapitału pokrywającego wymagane nakłady inwestycyjne,

FCF_i - projektowane przyszłe wolne przepływy pieniężne netto możliwe do osiągnięcia w kolejnych okresach eksploatacji inwestycji,

n - liczba przewidywanych okresów prognozy finansowej dla danej inwestycji.

F. Jeśli wartość NPV jest dodatnia, to dany projekt inwestycyjny należy zaakceptować do realizacji, ponieważ:

• generuje on sumę wartości bieżącej przyszłych przepływów pieniężnych wyższą od początkowego nakładu kapitałowego,

• przynosi wyższą od oczekiwanej stopę zwrotu z inwestycji,

• wypracowuje taką wartość dochodów, które umożliwiają pokrycie kosztu kapitału zaangażowanego w finansowanie przedsięwzięcia,

• tworzy nadwyżkę finansową, która może być wykorzystana do finansowania kolejnych przedsięwzięć inwestycyjnych przedsiębiorstwa,

• zwiększa zasoby przedsiębiorstwa,

• zwiększa wartość przedsiębiorstwa.

G. Przy ujemnym NPV inwestycję (lub rozpatrywany jej wariant) powinniśmy odrzucić jako nierentowną, gdyż przedsięwzięcie:

• w ustalonym okresie jego eksploatacji nie przynosi oczekiwanej przez inwestora stopy zwrotu od zainwestowanych kapitałów,

• nie zapewnia pokrycia kosztów kapitału finansującego dany projekt,

• nie generuje nadwyżki finansowej, czyli nie zwiększa zasobów przedsiębiorstwa,

• niszczy wartość podmiotu gospodarczego.

H. W sytuacji, gdy wszystkie rozpatrywane warianty projektów inwestycyjnych cechują się dodatnim wskaźnikiem NPV, do realizacji akceptuje się tę inwestycję lub ten wariant przedsięwzięcia, który dla tej samej wartości nakładów inwestycyjnych, przy poziomie tej samej oczekiwanej stopy zwrotu oraz dla tego samego okresu planowanej eksploatacji projektu tworzy największą wartość obecną netto. Innymi słowy, w wyborze najlepszego wariantu inwestycyjnego posługujemy się kryterium maksymalizacji miernika NPV, gdyż tylko takie przedsięwzięcie w największym stopniu zwiększa wartość przedsiębiorstwa.

I. Zaletami metody NPV są przede wszystkim następujące jego cechy:

• uwzględnianie w analizie opłacalności inwestycji zmiennej wartości pieniądza w czasie,

• możliwość wyboru takiego wariantu projektu inwestycyjnego, który daje lepsze efekty w sytuacji ograniczonej dla firmy dostępności do kapitałów,

• uwzględnienie w kalkulacji prognozowanych korzyści (przepływów pieniężnych) z całego planowanego okresu funkcjonowania (eksploatacji) projektu inwestycyjnego,

• jest obiektywnym kryterium ułatwiającym podejmowanie wszelkich decyzji inwestycyjnych,

• jest wskaźnikiem najlepiej opisującym możliwości firmy w realizacji strategii wzrostu wartości dla właścicieli.

J. Podstawowymi wadami metody NPV są następujące cechy tego wskaźnika:

• trudności w wyborze odpowiedniej stopy dyskontowej,

• przyjmowanie na ogół stałej oczekiwanej stopy zwrotu dla kolejnych okresów eksploatacji inwestycji,

• trudności w naliczaniu premii za ryzyko danego projektu inwestycyjnego,

• kłopoty w ustalaniu przyszłych możliwych do osiągnięcia wartości przepływów pieniężnych.

K. Miernik NPV może być obliczany w arkuszu kalkulacyjnym EXCEL przy wykorzystaniu wbudowanych w nim funkcji finansowych. Za pomocą tego programu komputerowego wartość NPV oblicza się deklarując następujący zapis funkcji:

= NPV (stopa dyskontowa; wartość FCF1; wartość FCF2 ...) + (- Io)

lub odwołując się do adresów komórek, przykładowo:

= NPV (A2; B1:F1) + A1

gdzie:

A2 - adres komórki arkusza kalkulacyjnego, w którym znajduje się wielkość oczekiwanej stopy zwrotu,

B1:F1 - adresy komórek w arkuszu kalkulacyjnym, w których znajdują się wartości prognozowanych przepływów pieniężnych,

A1 - adres komórki w arkuszu kalkulacyjnym, w której wpisana wartość nakładu inwestycyjnego (ze znakiem ujemnym).

PRZYKŁAD:

Na podstawie kryterium wartości obecnej netto (NPV) wybierz jeden spośród dwóch rozważanych projektów inwestycyjnych, planowanych do realizacji przez przedsiębiorstwo GRAB. Zarówno projekt A, jak i projekt B wymagają zaangażowania 1.500 tys. zł. Oceniono, że projekty te mogą w kolejnych pięciu latach wygenerować następujące wolne przepływy pieniężne (FCF):

ROK	PROJEKT A	PROJEKT B
1	300.000 zł	500.000 zł
2	400.000 zł	300.000 zł
3	500.000 zł	100.000 zł
4	600.000 zł	- 50.000 zł
5	700.000 zł	- 100.000 zł

Zakładany nakład inwestycyjny mógłby zostać sfinansowany kapitałami o średnim koszcie ich pozyskania równym 12% rocznie (taka jest minimalna oczekiwana roczna stopa zwrotu z przedsięwzięcia).

ROZWIĄZANIE:

Dane:

Io = 1.500.000 zł, r = 12% rocznie, wartości planowanych przepływów pieniężnych podane są w tabeli w treści przykładu

Projekt A:

=

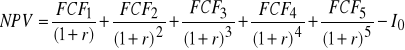
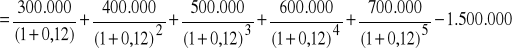
= 221.135 zł

Gdybyśmy chcieli skorzystać z arkusza kalkulacyjnego EXCEL, wówczas należałoby zdeklarować do obliczenia następującą funkcję:

= NPV (12%; A1:A5) - 1 500 000

Projekt B:

=

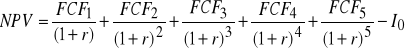
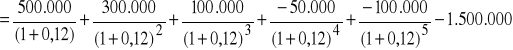
= - 831.754 zł

Gdybyśmy chcieli skorzystać z arkusza kalkulacyjnego EXCEL, wówczas należałoby zdeklarować do obliczenia następującą funkcję:

= NPV (12%; B1:B5) - 1 500 000

Z przedstawionych wyliczeń wynika, że projekt A powinien być przyjęty do realizacji. Przedsięwzięcie to cechuje się dodatnią wartością obecną netto, choć wymaga takiego samego nakładu inwestycyjnego jak nierentowny projekt B, planowane jest do eksploatacji w tym samym czasie co projekt konkurencyjny, finansowane jest jak projekt B kapitałami o koszcie pozyskania wynoszącym 12% rocznie. Projekt A, jeśli zostanie zrealizowany i przyniesie takie korzyści jak wynika z planu finansowego, zwiększy zasoby i wartość przedsiębiorstwa GRAB.

Wewnętrzna stopa zwrotu z inwestycji (IRR)

A. Wewnętrzna stopa zwrotu z inwestycji (IRR) jest definiowana jako stopa zwrotu od zainwestowanych kapitałów, która przynosi wartość obecną netto (NPV) przedsięwzięcia inwestycyjnego równą zero.

B. Wewnętrzna stopa zwrotu (IRR) jest także definiowana jako taka średnia okresowa stopa zyskowności projektu inwestycyjnego, przy której następuje zwrot poniesionych wydatków inwestycyjnych oraz pokrycie kosztu kapitału zaangażowanego w rozwój firmy.

C. Wewnętrzna stopa zwrotu (IRR) jest rozumiana również jako stopą dyskontową, przy której wartość obecna wydatków pieniężnych jest równa zaktualizowanej wartości przyszłych wpływów pieniężnych generowanych w całym okresie eksploatacji przedsięwzięcia inwestycyjnego. Przy tej stopie zwrotu wartość obecna efektów z inwestycji równa się wartości obecnej nakładów inwestycyjnych.

D. Wewnętrzna stopa zwrotu (IRR) może być w końcu zdefiniowana jako średnia w jednym okresie stopa dyskontowa, która zrównuje wartość obecną oczekiwanych wpływów środków pieniężnych z planowanego przedsięwzięcia z wartością obecną oczekiwanych wydatków na inwestycję.

E. Obliczona wewnętrzna stopa zwrotu (IRR) obrazuje graniczną stopę zwrotu możliwą do osiągnięcia z analizowanego przedsięwzięcia inwestycyjnego. Osiąganie później niższej stopy zwrotu niż wyznaczona stopa graniczna spowoduje, że dana inwestycja będzie dla firmy nieopłacalna - będzie przynosić jej straty finansowe.

F. Wewnętrzna stopa zwrotu (IRR) jest zwykle porównywana ze stopą średnio ważonego kosztu kapitału (WACC), a decyzja dotycząca inwestowania zapada według schematu:

• IRR > WACC - projektowaną inwestycję lub jej wariant można realizować; zarządzający podejmuje decyzję akceptującą realizację planowanego przedsięwzięcia, ponieważ projekt ten zwiększy wartość przedsiębiorstwa,

• IRR < WACC - należy zaniechać realizacji inwestycji lub jej wariantu, bowiem projekt ten jest dla firmy nieopłacalny; zarządzający podejmuje decyzje o odrzuceniu planowanego przedsięwzięcia, ponieważ projekt ten zmniejszy wartość przedsiębiorstwa,

• IRR = WACC - inwestycja może zostać podjęta, jednakże badane przedsięwzięcie jest dość ryzykowne i wrażliwe na zmienność czynników wpływających na poziom średnio ważonego kosztu kapitału (np. wielkości stopy oprocentowania kredytów); badany projekt jest obojętny w kształtowaniu wartości przedsiębiorstwa.

G. Wewnętrzną stopę zwrotu z inwestycji (IRR) można obliczyć rozwiązując następujące równanie:

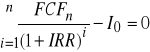
lub w wersji formuły rozszerzonej:

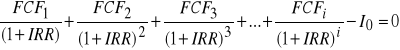
gdzie:

Io - wartość początkowego nakładu inwestycyjnego,

IRR - poszukiwana wewnętrzna stopa zwrotu z inwestycji,

FCF_i - projektowane przyszłe wolne przepływy pieniężne możliwe do osiągnięcia z inwestycji w kolejnych latach jej eksplotacji,

n - liczba zakładanych okresów prognozy przepływów pieniężnych możliwych do osiągnięcia z inwestycji.

H. Rozwiązanie równania określającego IRR nie zawsze jest proste, ponieważ w grę wchodzi zwykle równanie wielomianu wyższego rzędu. W praktyce stosuje się do ustalenia IRR programy komputerowe (np. arkusz kalkulacyjny EXCEL) lub kalkulatory finansowe. Korzystając z arkusza EXCEL należałoby zadeklarować programowi rozwiązanie następującej funkcji:

= IRR (wartość FCFo; wartość FCF1; ...; wartość FCFi)

lub odwołując się do adresów komórek, przykładowo:

= IRR (A1:F1)

gdzie:

A1:F1 - adresy komórek w arkuszu kalkulacyjnym, w których znajdują się wartości prognozowanych przepływów pieniężnych oraz początkowego nakładu inwestycyjnego (ze znakiem ujemnym).

I. Do głównych zalet miernika IRR zalicza się:

• uwzględnienie w kalkulacji zmiennej wartości pieniądza w czasie,

• przyjęcie do wyboru inwestycji obiektywnego kryterium, jakim jest stopa zwrotu,

• łatwość porównania ze sobą kilku projektów inwestycyjnych.

J. Wyróżnia się następujące wady wskaźnika IRR:

• możliwość wyboru przedsięwzięcia, które tworzy największą stopę zwrotu, ale przynosi relatywnie mniejszą wartość obecną netto niż inne projekty inwestycyjne; oznacza to, że posługując się kryterium IRR nie zawsze wybierze się działania inwestycyjne, które będą maksymalizować wartość przedsiębiorstwa,

• możliwość wystąpienia wielu IRR lub nie wystąpienia żadnej wielkości stopy zwrotu,

• trudność w liczeniu, jeśli nie wykorzystuje się w tym celu kalkulatora finansowego lub odpowiedniego oprogramowania komputerowego.

PRZYKŁAD:

Planujesz sfinansowanie inwestycji o wartości 1.350.000 zł. Szacujesz, że przedsięwzięcie to w kolejnych pięciu latach jego eksploatacji przyniesie ci wolne przepływy pieniężne netto o następujących wartościach: - 500.000 zł, 900.000 zł, 1.100.000 zł, 1.500.000 zł, - 350.000 zł. Oczekiwana przez ciebie stopa zwrotu z zaangażowanych kapitałów, równa kosztom kapitałów, które sfinansują inwestycję wynosi 15% rocznie. Jaką średnią roczną wewnętrzną stopę zwrotu osiągniesz z tego przedsięwzięcia i czy inwestycja ta jest dla ciebie opłacalna?

ROZWIĄZANIE:

Dane:

Io = 1.350.000 zł, FCF1 = - 500.000 zł, FCF2 = 900.000 zł, FCF3 = 1.100.000 zł, FCF4 = 1.500.000 zł, FCF5 = - 350.000 zł

Aby obliczyć IRR należy rozwiązać następujące równanie:

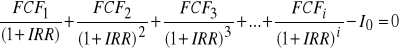
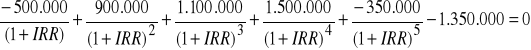
Korzystając z arkusza kalkulacyjnego EXCEL wpisujemy następującą funkcję:

= IRR (-1350000; -500000; 900000; 1100000; 1500000; -350000)

Otrzymujemy wynik równy:

IRR = 21,95%

Wewnętrzna stopa zwrotu z tego przedsięwzięcia (IRR) wyniesie około 22% średnio rocznie. Będzie większa od kosztu kapitału finansującego inwestycję (oczekiwanej stopy zwrotu) o około 7 pkt procentowych. Zatem planowane przedsięwzięcie może być podjęte do realizacji, bowiem jest opłacalne z punktu widzenia ekonomicznego.

Zmodyfikowana wewnętrzna stopa zwrotu z inwestycji (MIRR)

A. Zmodyfikowana wewnętrzna stopa zwrotu (MIRR) jest to taka stopa dyskontowa (stopa zwrotu z inwestycji), przy której łączna wartość przyszła wszystkich dodatnich przepływów pieniężnych możliwych do osiągnięcia z inwestycji będzie po ich zdyskontowaniu równa wartości obecnej wszystkich ujemnych przepływów pieniężnych związanych z danym przedsięwzięciem.

B. Zmodyfikowana wewnętrzna stopa zwrotu (MIRR) to inaczej taka stopa dyskontowa, która zrównuje wartość wpływów pieniężnych z inwestycji na koniec okresu danego projektu z sumą nakładów początkowych.

C. Zmodyfikowana wewnętrzna stopa zwrotu (MIRR) może być w końcu zdefiniowana jako wielkość stopy dyskontowej, dla której wartość bieżąca sumy reinwestowanych według sposobności rynkowych wpływów pieniężnych jest równa sumie wartości bieżącej wydatków.

D. W wyznaczaniu miernika MIRR wykorzystuje się dwie wielkości oczekiwanej stopy zwrotu: stopę kosztu kapitału oraz stopę reinwestycji.

E. Wszystkie ujemne przepływy pieniężne (nawet te z ich niekonwencjonalnego układu) są dyskontowane przy wykorzystaniu stopy kosztu kapitału firmy. W ten sposób bieżąca wartość ujemnych przepływów pieniężnych jest równa:

DCOF =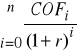

gdzie:

DCOF - zdyskontowane wszystkie ujemne przepływy pieniężne przewidywane dla danego projektu inwestycyjnego,

COFi - ujemne przepływy pieniężne w danym okresie,

r - wymagana przez inwestora stopa zwrotu równa kosztowi kapitału finansującego inwestycję.

F. Z kolei wszystkie dodatnie przepływy pieniężne możliwe do osiągnięcia z inwestycji w zakładanym okresie jej eksploatacji są kapitalizowane na koniec okresu prognozy finansowej ustaloną oczekiwaną stopą reinwestycji (reivestment assumption). Najczęściej przyjmuje się, że stopa przy której będą reinwestowane osiągane z przedsięwzięcia nadwyżki wpływów nad wydatkami odpowiada docelowej stopie kosztu kapitału przedsiębiorstwa. Oczywiście inwestor może przyjąć inną stopę reinwestycji, na przykład związaną z poziomem rentowności długoterminowych obligacji skarbowych (wolna od ryzyka stopa zwrotu). Łączna wartość przyszła skapitalizowanych dodatnich przepływów pieniężnych nosi nazwę wartości terminowej lub końcowej (terminal value - TV). Oblicza się ją według formuły:

TV =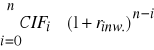

gdzie:

CIFi - dodatnie przepływy pieniężne z danego okresu,

- przyjęta przez inwestora stopa reinwestycji dodatnich przepływów pieniężnych,

pozostałe oznaczenia jak w poprzednim wzorze.

G. Następnie poszukuje się takiej stopy zwrotu, która zrównałaby wartość obecną wszystkich dodatnich i reinwestowanych przepływów pieniężnych (TV) z wartością obecną wszystkich ujemnych przepływów pieniężnych (DCOF). Ta poszukiwana stopa zwrotu jest określana jako MIRR. Obliczenie jej wartości można zapisać jako rozwiązanie następującego równania:

=

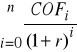
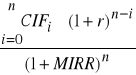
lub prościej:

DCOF =

Wynika z tego, że zmodyfikowaną wewnętrzną stopę zwrotu z inwestycji (MIRR) wylicza się z następującego wzoru:

gdzie:

oznaczenia jak w poprzednich wzorach.

H. Wielkość zmodyfikowanej wewnętrznej stopy zwrotu (MIRR) można również ustalić wykorzystując arkusz kalkulacyjny EXCEL. Należy w tym przypadku wpisać do komputera następujące równanie:

= MIRR (FCF 0:FCFn; stopa dyskontowa; stopa reinwestycji)

lub odnosząc się do adresów komórek:

= MIRR (A1:A6; B1; C1)

gdzie:

A1:A6 - projektowane dla danej inwestycji przepływy pieniężne począwszy od okresu 0,

B1 - stopa dyskontowa (oczekiwana stopa zwrotu, stopa kosztu kapitału),

C1 - stopa reinwestycji.

I. Zasady decyzyjne w przypadku zastosowania zmodyfikowanej wewnętrznej stopy zwrotu (MIRR) są podobne jak przy stosowaniu wskaźnika IRR. Zatem, jeśli:

• MIRR jest większa od oczekiwanej stopy zwrotu (kosztu kapitału), to taki projekt inwestycyjny powinien zostać zaakceptowany do realizacji,

• MIRR jest mniejsza od oczekiwanej stopy zwrotu (kosztu kapitału), to taki projekt inwestycyjny powinien zostać odrzucony jako niereentowny.

J. Do podstawowych zalet wskaźnika MIRR zalicza się:

• jednoznaczność uzyskanego wyniku (stopa MIRR jest zawsze jedna, nie ma więc problemu jej wielokrotności, jak bywa w przypadku kryterium IRR),

• uwzględnianie zmiany wartości pieniądza w czasie,

• stopa kapitalizacji stosowana w tej metodzie jest bardziej uzasadniona niż ta, która występuje przy IRR.

K. Za wadę MIRR uważa się fakt, iż stosując ten miernik można wybrać taki projekt inwestycyjny, który nie będzie maksymalizował wartości przedsiębiorstwa. Zawsze w takich okolicznościach konieczna jest weryfikacja przedsięwzięcia kryterium wartości obecnej netto (NPV).

PRZYKŁAD:

Ustal zmodyfikowaną wewnętrzną stopę zwrotu (MIRR) z inwestycji o planowanym okresie eksploatacji wynoszącym 5 lat, opisanej następującymi zmiennymi:

• wartość początkowego nakładu inwestycyjnego wyniesie 750.000 zł,

• w latach nieparzystych (czyli w roku 1, 3 i 5) inwestycja wygeneruje dodatnie wolne przepływy pieniężne o wartości 950.000 zł w każdym z tych okresów,

• w latach parzystych (czyli w roku 2 i 4) inwestycja będzie deficytowa i przyniesie ujemne przepływy pieniężne o wartości 350.000 zł w każdym z tych okresów.

Oczekiwana stopa zwrotu z tego przedsięwzięcia (koszt kapitału) została ustalona na 10% rocznie, natomiast stopa reinwestycji równa stopie rentowności długoterminowych obligacji skarbowych jest równa 6%.

ROZWIĄZANIE:

Dane:

COFo = 750.000 zł, COF2 = 350.000 zł, COF4 = 350.000 zł

CIF1 = 950.000 zł, CIF3 = 950.000 zł, CIF5 = 950.000 zł

r = 10% rocznie, rinw. = 6% rocznie, n = 5 lat

Najpierw obliczymy łączną zdyskontowaną wartość ujemnych przepływów pieniężnych (COF):

DCOF =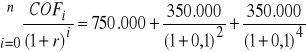
= 1.278.311 zł

Następnie obliczymy łączną wartość końcową kapitalizowanych dodatnich przepływów pieniężnych:

TV =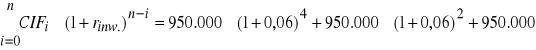
=

= 3.216.773 zł

Znając te wartości możemy obliczyć MIRR korzystając z następującej zależności:

= 0,203 (20,3%)

Wynika z tego, że zmodyfikowana wewnętrzna stopa zwrotu dla tego przedsięwzięcia jest większa od oczekiwanej stopy zwrotu (kosztu kapitału), a więc inwestycja ta może być zaakceptowana do realizacji.

Indeks zyskowności inwestycji

A. Indeks zyskowności inwestycji (Profitable Index - PI), nazywany również wskaźnikiem dochodowości lub rentowności przedsięwzięcia jest rozumiany jako relacja wartości obecnej przepływów pieniężnych możliwych do osiągnięcia w przyszłych okresach eksploatacji planowanego projektu i wartości początkowego nakładu inwestycyjnego. W tym kontekście indeks zyskowności inwestycji (PI) oblicza się według następującej formuły:

+ 1

gdzie:

PI - indeks zyskowności,

Io - początkowy nakład inwestycyjny,

NPV - wartość obecna netto dla danego projektu inwestycyjnego.

B. Przydatność zastosowania indeksu zyskowności występuje głównie wtedy, gdy oceniający inwestycje chce porównać ze sobą kilka projektów cechujących się zróżnicowaną wartością początkowego nakładu kapitałowego i są to przy okazji przedsięwzięcia wzajemnie wykluczające się. Jeśli nawet są to inwestycje finansowane funduszami pozyskanymi przy tym samym koszcie kapitałowym, mogące generować wolne przepływy pieniężne w tym samym okresie zakładanej ich eksploatacji, ale różnią się kwotą nakładu, to wartości NPV ustalone dla nich będą odmienne. Wybór właściwego projektu staje się więc utrudniony. W takich okolicznościach, posługując się indeksem zyskowności menedżer finansowy może wyselekcjonować to przedsięwzięcie, które w rzeczywistości będzie maksymalizować korzyści finansowe przedsiębiorstwa.

C. Przy wyborze indeksem zyskowności właściwego wariantu inwestycji kierujemy się następującym schematem decyzyjnym:

• jeśli PI jest większy od jedności, to dana inwestycja jest opłacalna i można ją zrealizować,

• jeśli PI jest mniejszy od jedności, to rozpatrywany projekt inwestycyjny należy odrzucić jako nierentowny.

Jeśli dla wszystkich rozpatrywanych projektów otrzymujemy indeksy zyskowności większe od jedności, wybieramy ten wariant przedsięwzięcia, który przynosi nam większą jego wielkość.

PRZYKŁAD:

Inwestor ma do wyboru dwa wzajemnie wykluczające się projekty inwestycyjne, które byłyby eksploatowane w tym samym okresie, i dla których charakterystyki finansowe przedstawia poniższe zestawienie (wartości w złotych):

OKRES (ROK)	PROJEKT A	PROJEKT B
0	-1.000.000	-750.000
1	300.000	400.000
2	500.000	500.000
3	700.000	600.000
4	900.000	700.000
5	1.100.000	800.000

Ze względu na to, iż ryzyko każdego z tych przedsięwzięć jest takie samo, koszt kapitału, który sfinansowałby którykolwiek z rozważanych projektów został ustalony na 10% rocznie.

Dokonaj wyboru bardziej opłacalnej inwestycji.

ROZWIĄZANIE:

Najpierw spróbujmy wybrać lepszy projekt inwestycyjny posługując się kryterium wartości obecnej netto (NPV):

NPV (projekt A) = 1.509.596 zł

NPV (projekt B) = 1.452.495 zł

Metoda NPV wskazuje, że powinniśmy przyjąć projekt A, ponieważ może przynieść inwestorowi większą wartość korzyści finansowych. Jednakże wiemy, że projekt ten wymaga większego zaangażowania kapitałowego. W celu bardziej wiarygodnej analizy oceńmy oba przedsięwzięcia indeksem zyskowności:

2,51

2,94

Projekt B cechuje się wyższym wskaźnikiem zyskowności i to on powinien zostać wybrany do realizacji.

Zdyskontowany okres zwrotu

A. Zdyskontowany okres zwrotu definiowany jest jako liczba lat, po których zdyskontowane i skumulowane przepływy pieniężne osiągane z inwestycji będą równały się wartości początkowego nakładu kapitałowego.

B. Zdyskontowany okres zwrotu można także określić jako okres, po jakim nastąpi zrównanie wartości bieżącej wpływów z wartością bieżącą wydatków.

C. Wadą tego miernika jest to, że nie informuje on inwestora o możliwej do osiągnięcia stopie zwrotu z rozważanego przedsięwzięcia.

PRZYKŁAD:

Dla przepływów pieniężnych z poprzedniego przykładu wyznacz zdyskontowane okresy zwrotu rozważanych projektów inwestycyjnych.

ROZWIĄZANIE:

Najłatwiej będzie wyznaczyć zdyskontowany okres zwrotu posługując się zestawieniem tabelarycznym (dane w złotych):

PROJEKT A

OKRES	PRZEPŁYWY PIENIĘŻNE	ZDYSKONTOWANE PRZEPŁYWY PIENIĘŻNE (r = 10%)	SKUMULOWANE ZDYSKONTOWANE PRZEPŁYWY PIENIĘŻNE
0	-1.000.000	-1.000.000	-1.000.000
1	300.000	272.727	-727.273
2	500.000	413.223	-314.050
3	700.000	525.920	211.870
4	900.000	614.712	826.582
5	1.100.000	683.013	1.509.595

Zdyskontowany okres zwrotu = 2 + (314.050 / 525.920) = 2,6 roku

PROJEKT B

OKRES	PRZEPŁYWY PIENIĘŻNE	ZDYSKONTOWANE PRZEPŁYWY PIENIĘŻNE (r = 10%)	SKUMULOWANE ZDYSKONTOWANE PRZEPŁYWY PIENIĘŻNE
0	-750.000	-750.000	-750.000
1	400.000	363.636	-386.364
2	500.000	413.223	26.859
3	600.000	450.789	477.648
4	700.000	478.109	955.575
5	800.000	496.737	1.452.494

Zdyskontowany okres zwrotu = 1 + (386.364 / 413.223) = 1,94 roku

Jeśli dwa rozpatrywane projekty są wzajemnie wykluczające się, to do realizacji powinno być zaakceptowane przedsięwzięcie B, gdyż charakteryzuje się krótszym zdyskontowanym okresem zwrotu.

Wartość wpisana w nawiasie, to wartość ujemna. W tym przykładzie chodzi o wartość wydatku inwestycyjnego (wypływu środków kapitałowych niezbędnych na pokrycie nakładu inwestycyjnego).

Por. E.F. Brigham, L.C. Gapenski, Zarządzanie finansami, tom I, PWE, Warszawa 2000, s. 303.

Por. D.J. Leahigh, Zarządzanie finansami, PWE, Warszawa 1999, s. 83.

Por. A. Rutkowski, Zarządzanie finansami, PWE, Warszawa 2000, s. 224.

Por. dyskusję na ten temat w: E.F. Brigham, L.C. Gapenski, Zarządzanie finansami, tom I, op. cit., s. 313 i 320.

Por. A. Rutkowski, Zarządzanie finansami, op. cit., s. 216.

15

---