Jacek Finster 27- 11- 2000

Nr ćwiczenia: B-16

Temat ćwiczenia: Wyznaczenie rzędu reakcji metodą graficzną.

1. Wyniki pomiarów:

Pomiar ekstynkcji dla anionu kompleksowego [ Mn ( C₂O₄ )₃ ]^3- w czasie rozpadu tego anionu przy długości fali _max = 440 nm do osiągnięcia ok. 40 % wartości początkowej (pomiar przeprowadzony trzykrotnie).

L.p.	Czas, t [min]	EI	EII	EIII
1	0	____________________	____________________	____________________
2	5	____________________	____________________	____________________
3	10	____________________	____________________	____________________
4	15	____________________	____________________	____________________
5	20	____________________	____________________	____________________
6	25	____________________	____________________	____________________
7	30	____________________	____________________	____________________
8	35	____________________	____________________	____________________
9	40	____________________	____________________	____________________
10	45	____________________	____________________	____________________

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

-1-

2. Wstęp teoretyczny:

Podstawowymi parametrami kinetycznymi charakteryzującymi daną reakcję chemiczną są stała szybkości i rząd reakcji.

Szybkość reakcji jest to ubytek stężenia substratu (znak minus w równaniu) lub przyrost stężenia produktu w czasie trwania reakcji. Podstawowe równanie kinetyczne przedstawia zależność:

c- stężenie substratu

x- stężenie produktu

O całkowitej szybkości reakcji decyduje najpowolniejszy etap tej reakcji. Szybkość reakcji zależy od stężenia poszczególnych reagentów. Jeżeli np. w reakcji biorą udział trzy substraty: A, B, C wówczas szybkość reakcji jest równa:

Współczynniki potęgowe a, b, c są charakterystyczne dla danej reakcji. Każdy współczynnik określa rząd reakcji względem danego reagenta. Suma współczynników potęgowych określa sumaryczny rząd reakcji. Wyznaczenie rzędu reakcji jest konieczne przy badaniu mechanizmów, ponieważ każda reakcja może przebiegać poprzez szereg etapów i produktów pośrednich. Rząd reakcji może być ułamkowy, a także zerowy. W praktyce rząd reakcji zwykle nie jest większy od 3.

Liczbę cząsteczek biorących udział w reakcji elementarnej nazywa się cząsteczkowością reakcji. Ze względu na prawdopodobieństwo wzajemnego zderzenia cząsteczkowość ogranicza się do 2, rzadziej 1 i bardzo rzadko 3 cząsteczek.

W przypadku reakcji I rzędu równanie kinetyczne ma postać:

Po całkowaniu otrzymuje się:

c₀- stężenie początkowe

Zamieniając logarytmy naturalne na dziesiętne równanie przyjmuje postać:

-2-

Dla reakcji I rzędu charakterystyczna jest liniowa zależność log c od czasu. Stałą szybkości k można wyznaczyć z nachylenia prostej log c = f ( t ).

W przypadku reakcji II rzędu równanie kinetyczne ma postać:

Po odpowiednich przekształceniach dla reakcji II rzędu dostaje się liniową zależność odwrotności stężenia w funkcji czasu:

W przypadku reakcji III rzędu równanie kinetyczne ma postać:

Przekształcając podobnie jak poprzednie równania dochodzi się do wniosku, że liniowo od czasu zależy odwrotność kwadratu stężenia substratu:

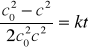
W graficznej metodzie wyznaczania rzędu reakcji wykorzystuje się scałkowane postacie równań kinetycznych i przedstawienie wyników pomiarów na wykresie.

Dla reakcji I rzędu liniowa jest zależność między log c i czasem, dla reakcji II rzędu liniowa jest zależność między odwrotnością ze stężenia i czasem, a dla reakcji III rzędu- liniowa zależność między kwadratem odwrotności ze stężenia i czasem.

3. Część doświadczalna:

Celem ćwiczenia jest graficzne wyznaczenie rzędu i stałej szybkości dla reakcji rozpadu kompleksowego anionu szczawianu manganu. Reakcja rozpadu zachodzi zgodnie z równaniem:

[ Mn ( C₂O₄ )₃ ]^3- Mn²⁺ + 5/2 C₂O₄^2- + CO₂

Ponieważ barwny kompleks rozpada się na bezbarwne produkty, zmiany stężenia można badać metodą spektrofotometryczną przez pomiar ekstynkcji (absorbancji).

Z prawa Lamberta- Beera wynika, że ekstynkcja jest proporcjonalna do stężenia. Można więc w równaniu kinetycznym zastąpić stężenie ekstynkcją, którą odczytuje się wprost ze skali spektrofotometru:

Jeżeli przebieg zależności log E od czasu jest prostoliniowy wówczas reakcja jest I rzędu.

-3-

Stała szybkości reakcji wyznaczona z powyższego równania wynosi:

k- stała szybkości reakcji [s^-1]

log E₀- logarytm dziesiętny początkowej wartości ekstynkcji

log E- logarytm dziesiętny kolejnej wartości ekstynkcji

t- czas [s]

Obliczenia na podstawie uzyskanych wyników pomiarów:

1. Seria I:

L.p.	Czas [min]	Czas [s]	Ei	log Ei	k
1.	0	0	1,05	0,0212	---
2.	5	300	0,57	-0,2441	2,04 * 10^-3
3.	10	600	0,31	-0,5086	2,03 * 10^-3
4.	15	900	0,19	-0,7212	1,90 * 10^-3
5.	20	1200	0,10	-1,0000	1,96 * 10^-3
6.	25	1500	0,06	-1,2218	1,91 * 10^-3

Średnia wartość stałej szybkości reakcji dla serii I k= 1,97 * 10^-3

2. Seria II

L.p.	Czas [min]	Czas [s]	EII	log EII	k
1.	0	0	1,05	0,0212	---
2.	5	300	0,51	-0,2924	2,41 * 10^-3
3.	10	600	0,31	-0,5086	2,03 * 10^-3
4.	15	900	0,18	-0,7447	1,96 * 10^-3
5.	20	1200	0,09	-1,0457	2,05 * 10^-3
6.	25	1500	0,06	-1,2218	1,91 * 10^-3

Średnia wartość stałej szybkości reakcji dla serii II k= 2,07 * 10^-3

-4-

3. Seria III

L.p.	Czas [min]	Czas [s]	EIII	log EIII	k
1.	0	0	1,05	0,0212	---
2.	5	300	0,53	-0,2757	2,28 * 10^-3
3.	10	600	0,28	-0,5528	2,20 * 10^-3
4.	15	900	0,19	-0,7212	1,90 * 10^-3
5.	20	1200	0,09	-1,0457	2,05 * 10^-3
6.	25	1500	0,05	-1,3010	2,03 * 10^-3

Średnia wartość stałej szybkości reakcji dla serii III k= 2,09 * 10^-3

___________________________________________________________________________

Średnia wartość stałej szybkości reakcji dla serii I	k= 1,97 * 10^-3
Średnia wartość stałej szybkości reakcji dla serii II	k= 2,07 * 10^-3
Średnia wartość stałej szybkości reakcji dla serii III _________________________________________	k= 2,09 * 10^-3 ___________
Wartość średnia stałej szybkości dla serii I, II, III	k= 2,04 * 10^-3

Aby określić błąd występujący w pomiarach wyznaczam przedział ufności. Przyjmuję poziom istotności =0,05. Wartość średnia stałej szybkości reakcji k= 2,04 * 10^-3. Odchylenie standardowe wynosi 0,07 * 10^-3. Przedział ufności dla powyższych wartości jest równy 0,08 * 10^-3. Stała szybkości reakcji rozkładu szczawianu manganu wynosi 2,04 * 10^-3 ± 0,07 * 10^-3.

Reakcja rozpadu kompleksowego anionu [Mn(C₂O₄)₃]^3- jest reakcją pierwszego rzędu. Świadczy o tym liniowy przebieg zależności log E = f (t).

Najwolniejszym etapem decydującym o kinetyce reakcji redukcji KMnO₄ za pomocą (COOH)₂ jest rozpad kompleksu szczawianu manganu. Kompleks [Mn(C₂O₄)₃]^3- jest kompleksem barwnym. W miarę rozkładu barwa stopniowo zanika. Kompleks rozpada się na bezbarwne produkty, stężenie [Mn(C₂O₄)₃]^3- stopniowo maleje.

Mierzonym parametrem jest ekstynkcja. Ekstynkcja jest wprost proporcjonalna do stężenia substancji absorbującej. Grubość warstwy absorbującej ( l ) jest stała i równa 1 cm (dla tego przypadku).

Ponieważ zgodnie z prawem Lamberta- Beera ekstynkcja jest związana ze stężeniem można w metodzie graficznej wykorzystać bezpośrednio jej wartość do wyznaczenia rzędu reakcji i stałej szybkości reakcji.

-5-

Wyznaczenie rzędu reakcji metodą graficzną:

Do obliczeń biorę średnią wartość ekstynkcji z poszczególnych serii:

L.p.	Czas, t[s]	EI	EII	EIII	Eś®	log Eśr
1	0	1,05	1,05	1,05	1,050	0,0212
2	300	0,57	0,51	0,53	0,537	-0,2703
3	600	0,31	0,31	0,28	0,300	-0,5229
4	900	0,19	0,18	0,19	0,187	-0,7289
5	1200	0,1	0,09	0,09	0,093	-1,0299
6	1500	0,06	0,06	0,05	0,057	-1,2467

Równanie regresji dla prostej log E_śr = f (t):

Współczynnik R- kwadrat wynosi 0,9977

Średni błąd kwadratowy nachylenia (a)= 0,00002

a= -0,00084 ± 0,00002

Ponieważ:

więc:

y= log E

x= t

b= log E₀= 0,00072 (przecięcie)

a= (-k / 2,303)= -0,00084 ± 0,00002 (nachylenie)

k= 1,93 * 10^-3 ± 0,05 * 10^-3

Stała szybkości reakcji rozkładu szczawianu manganu wyznaczona metodą graficzną wynosi 1,93 * 10^-3 ± 0,05 * 10^-3.

-7-

---