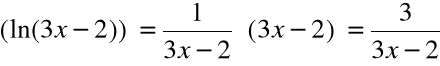Pochodna funkcji złożonej

y=f [g(x)], u=g(x):

Przykłady

1. (sin2x)′ = [u=2x] = cosu ⋅(u) ′ = cos2x ⋅(2x) ′ = =2cos2x

2. (cos(5x+1))′ = [u = 5x+1] = -sinu⋅(u)′= -sin(5x+1) ⋅(5x+1)′= -5sin(5x+1)

3. 
   

REGUŁY DE L'HOSPITALA

Twierdzenie

Jeśli:

1) funkcje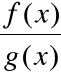
i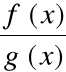
są określone w pewnym sąsiedztwie S punktu x₀;

2)

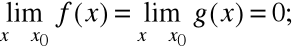
3) istnieje granica (właściwa lub nie właściwa):

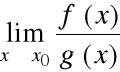
to istnieje również granica:

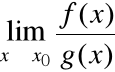
oraz

=

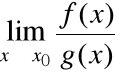
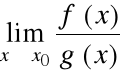
Przykład

Obliczyć granicę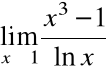

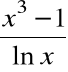
jest
dla x=1

=

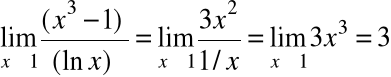
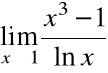
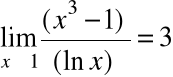
Twierdzenie

Jeśli:

1) funkcje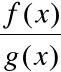
i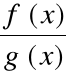
są określone w pewnym sąsiedztwie +∝;

2)

3) istnieje granica (właściwa lub nie właściwa):

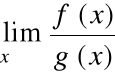
to istnieje również granica:

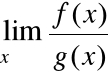
oraz

=

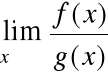
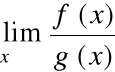
Przykład 1

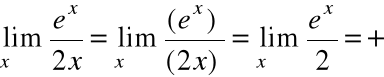
Przykład 2

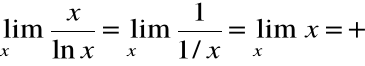
POCHODNE WYŻSZYCH RZĘDÓW

Definicje

Pochodną funkcji f ′(x), tzn. funkcje (f ′)′, którą oznaczamy przez f ′′, nazywamy drugą pochodną (lub pochodną drugiego rzędu) funkcji f(x).

Analogicznie (f ′′)′ = f ′′′ - trzecia pochodną (lub pochodną trzeciego rzędu) funkcji f(x).

(f ^(n-1))′ = f ⁽ⁿ⁾ - pochodną rzędu n funkcji f(x).

Przykład

f(x) = x³ +3x² - 5x +12

f ′(x) = 3x² +6x - 5

f ′′(x) = 6x+6

f ′′′(x) = 6

f ^(iv)(x) = 0

Różniczka funkcji

Definicja

Różniczką funkcji f(x) w punkcie x₀ ze względu na przyrost h nazywamy iloczyn f ′(x₀)h i oznaczamy df(x₀), tzn.

df(x₀) = f ′(x₀)h

Jeśli f(x) = x, to dx=1⋅h = h.

Zatem:

df(x₀) = f ′(x₀) ⋅dx

skąd:

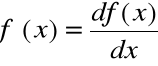
df(x) ≈ Δf(x),

gdzie Δf(x) = f(x+h) - f(x) - przyrost funkcji f(x).

---