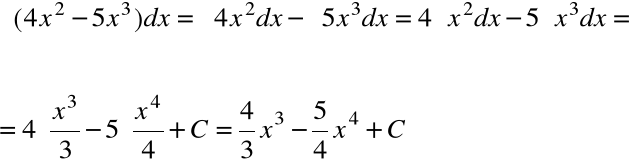Całka nieoznaczona

1. Pojęcie funkcji pierwotnej

Definicje

Funkcją pierwotną danej funkcji f(x) na przedziale X nazywamy każdą różniczkowaną funkcję F(x), której pochodna F ′(x) jest równa funkcji f(x) na tym przedziale, tj. gdy

F ′(x) = f(x) dla ∀x ∈X.

Przykłady

1. f(x) = cosx

F(x) = sinx, ponieważ F ′(x) = cosx = f(x).

2. f(x) = 3/2

F(x) =
, ponieważ F ′(x) = (
) ′ = 3/2
= f(x).

Definicje

Funkcję f mającą w pewnym przedziale funkcję pierwotna nazywamy całkowalną (w sensie Newtona) na tym przedziale.

Wyznaczenie funkcji pierwotnej danej funkcji f(x) nazywamy całkowaniem funkcji f(x).

Warunek wystarczający całkowania funkcji

Każda funkcja ciągła na przedziale X ma w tym przedziale funkcję pierwotną.

Twierdzenie

Jeśli F(x) jest funkcją pierwotną funkcji f(x), to

• funkcja ϕ(x) = F(x) + C, gdzie C ∈ R, jest także funkcją pierwotną funkcji f(x);

• każda funkcja pierwotna ϕ(x) funkcji f(x) da się przedstawić w postaci F(x) + C.

2. Całka nieoznaczona

Definicje

Zbiór wszystkich funkcji pierwotnych funkcji f(x) na przedziale X nazywamy całką nieoznaczoną funkcji f(x) na przedziale X i oznaczamy symbolem:

przy tym ∫ nazywamy symbolem całki, f(x)dx - wyrażeniem podcałkowym, a f(x) - funkcją podcałkową.

Podstawowy wzór rachunku całkowego:

= F(x) + C,

gdzie F(x) jest dowolną ustaloną funkcją pierwotną funkcji f(x) na przedziale X, a C - dowolna stałą, zwana stałą całkowania.

Przykłady

1.

2.

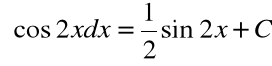
Twierdzenie ( o pochodnej całki )

Pochodna całki nieoznaczonej jest równa funkcji podcałkowej, tzn.

(
)′ = f(x).

Przykłady

1.

ponieważ

(x² + C)′ = 2x

2.

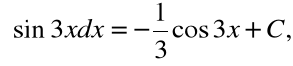
ponieważ

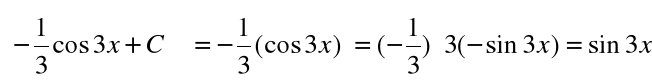
Twierdzenie ( całka pochodnej )

Całka nieoznaczona pochodnej funkcji jest sumą tej funkcji i dowolnej stałej, tzn.

= f(x) + C.

Przykłady

1.

2.

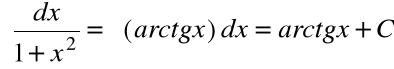
3. Podstawowe wzory

1.

2.

3.

4.

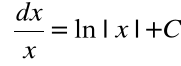
5.

6.

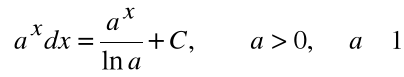
7.

8.

9.

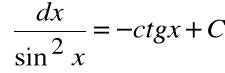
10.

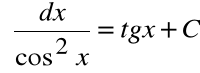
11.

12.

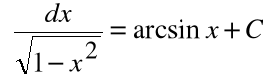
13.

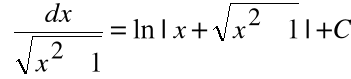
Wyłączanie czynnika stałego

Przykłady

1.

2.

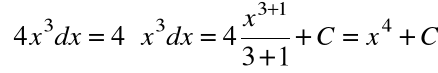
Całka sumy i różnicy

Przykłady

1.

=

2.

---