LOGIKA Wykład VII 11.05.2002

Formy zdaniowe

Formy zdaniowe dzielimy na trzy klasy:

• klasa P (prawda) - do klasy P należą te i tylko te formy zdaniowe, które są spełnione (prawdziwe) dla każdej wartości zmiennej należącej do zakresu, np.:

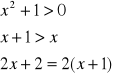
• klasa F (fałsz) - tylko te formy, które są fałszywe dla każdej wartości zmiennej należącej do zakresu, np.:

• klasa T (tylko) - te formy, które są spełnione tylko dla pewnych wartości zmiennych, np.:

Lp.	p(x)	q(x)
1)	P	P	P	P	P	P	F
2)	P	F	P	F	F	F	F
3)	P	T	P	T	T	T	F
4)	F	P	P	F	P	F	P
5)	F	F	F	F	P	P	P
6)	F	T	T	F	P	T	P
7)	T	P	P	T	P	T	T
8)	T	F	T	F	T	T	T
9)	T	T	T,P	T,F	T,P	T,P,F	T

• z dwóch koniunkcji klasy T nie można ułożyć koniunkcji klasy P

• z dwóch alternatyw klasy T nie można ułożyć alternatywy klasy F

• implikacja dwóch klas T nie może być klasy F

• równoważność dwóch klas T może być klasy P,F,T.

Tautologia (prawo) w rachunku form zdaniowych jest to wyrażenie złożone, które przy dowolnym wartościowaniu form zdaniowych w nim występujących należy zawsze do klasy P.

Zadanie I

Sprawdzić, czy podana forma zdaniowa jest tautologią.

Lp.	p(x)	q(x)	L1(x)	~q(x)	L2(x)	L(x)	P(x)	L(x)=>P(x)
1)	P	P	P	F	F	F	F	P
2)	P	F	F	P	P	F	F	P
3)	P	T	T	T	T	F	F	P
4)	F	P	P	F	P	P	P	P
5)	F	F	P	P	P	P	P	P
6)	F	T	P	T	P	P	P	P
7)	T	P	P	F	T	T	T	P
8)	T	F	T	P	P	T	T	P
9)	T	T	T,P	T	T,P	T	T	P

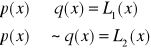
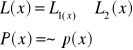
Odp. Podana forma zdaniowa jest tautologią.

Rozwiązanie metodą uproszczoną:

sprzeczność

---