Analiza wyników matury 2007 - matematyka

PESEL	Zad 1	Zad 2	Zad 3	Zad 4	Zad 5	Zad 6	Zad 7	Zad 8	Zad 9	Zad 10	Zad 11	Liczba punktów	Wynik %	Obowiązkowy
zdający 1	0	2	4	0	0	0	0	0	0	0	1	7	14%	T
zdający 2	3	2	3	0	0	2	0	4	2	5	4	25	50%	T
zdający 3	1	3	3	1	0	0	0	0	1	4	0	13	26%	T
zdający 4	2	3	4	0	2	4	5	2	5	4	2	33	66%	T
zdający 5	2	3	3	5	1	2	3	3	5	5	4	36	72%	T
zdający 6	0	1	4	1	1	4	0	2	6	4	2	25	50%	T
zdający 7	5	0	3	0	5	2	3	1	6	4	0	29	58%	T
zdający 8	0	2	3	0	1	1	0	3	2	2	2	16	32%	T
zdający 9	4	3	4	0	0	2	0	4	2	3	2	24	48%	T
zdający 10	5	3	3	1	0	2	4	0	5	3	2	28	56%	T
zdający 11	1	2	3	0	0	1	2	1	4	0	2	16	32%	T
zdający 12	0	2	4	0	1	2	2	0	2	2	0	15	30%	T
	38,3%	72,2%	85,4%	13,3%	18,3%	45,8%	31,7%	41,7%	55,6%	60,0%	43,8%

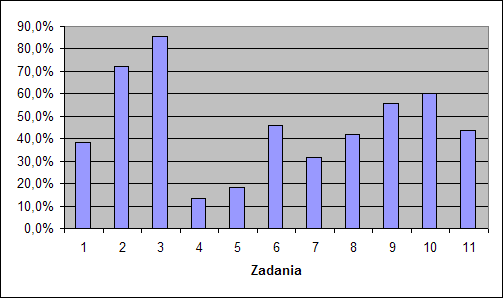
Zadania zawarte w arkuszach egzaminacyjnych sprawdzały wiadomości i umiejętności określone w 3 obszarach standardów wymagań egzaminacyjnych:

I. Wiadomości i rozumienie

II. Korzystanie z informacji

III. Tworzenie informacji.

Zadania zawarte w arkuszach egzaminacyjnych:

1) pozwalały wykazać się znajomością i rozumieniem podstawowych pojęć, definicji i twierdzeń oraz umiejętnością ich stosowania podczas rozwiązywania problemów matematycznych,

2) sprawdzały umiejętność analizowania i interpretowania tekstów matematycznych, sprawność rozwiązywania zadań, oraz przetwarzania informacji pochodzących z różnych źródeł, takich jak tabele, schematy, wykresy,

3) sprawdzały umiejętność analizowania i rozwiązywania problemów, argumentowania i prowadzenia rozumowania typu matematycznego, podawania opisu matematycznego danej sytuacji, dobierania algorytmów do wskazanej sytuacji problemowej i oceniania przydatności otrzymanych wyników.

Arkusz egzaminacyjny dla poziomu podstawowego zawierał 11 zadań otwartych. Zadania te badały przede wszystkim znajomość i rozumienie podstawowych pojęć matematycznych, definicji i twierdzeń oraz umiejętność posługiwania się tą wiedzą w praktyce. Sprawdzały umiejętność analizowania i interpretowania problemów matematycznych oraz formułowania opisu matematycznego danej sytuacji. Tematyka zadań egzaminacyjnych w tym arkuszu obejmowała większość treści z podstawy programowej. Najliczniej były reprezentowane zadania dotyczące ciągów, funkcji i ich własności, wielomianów, planimetrii i stereometrii z zastosowaniem trygonometrii oraz zadania z tzw. kontekstem praktycznym.

Arkusz I z poziomu podstawowego, okazał się dla naszych maturzystów przeciętny. Porównując wyniki wszystkich zdających w naszej szkole z wynikami wszystkich zdających maturę w maju 2007, otrzymaliśmy wynik średni 44,5% , wynik średni w kraju wyniósł 42%, a więc można powiedzieć, że wypadliśmy trochę lepiej niż przeciętna szkoła. Pozytywnym jest fakt, że wyniki matury z matematyki w naszej szkole w ostatnich latach mają tendencję zwyżkową. Niestety średnia poniżej 50% nie może być zadawalająca i trzeba nadal pracować nad poprawianiem wyników na egzaminie maturalnym.

Najlepsze wyniki osiągnęli uczniowie w zadaniach nr 2 i nr 3.

W zadaniu nr 2 były badane umiejętności:

• odczytywania z tabeli prostych informacji ilościowych i jakościowych.

• poprawnego wybierania modelu matematycznego i zastosowania go do rozwiązania problemu oraz wykonywania obliczeń procentowych i obliczeń na liczbach rzeczywistych.

Zdający poprawnie odczytywali potrzebne informacje z podanej w zadaniu tabeli, obliczali wartość transakcji kupna i sprzedaży, prowizje, które należy zapłacić w biurze maklerskim i prawidłowo zapisywali wyrażenie arytmetyczne, za pomocą którego można obliczyć zysk z transakcji. Było to typowe zadanie praktyczne z wykorzystaniem obliczeń procentowych. Najważniejszą umiejętnością badaną w tym zadaniu było czytanie ze zrozumieniem tekstu matematycznego. Mimo, iż zadania dotyczące obliczeń procentowych związanych z kredytami i lokatami są obecne w nauczaniu matematyki na poziomie gimnazjum i szkoły ponadgimnazjalnej, to niektórzy zdający mieli problemy ze zrozumieniem pojęcia prowizji i zysku.

W zadaniu 3 były badane następujące umiejętności:

• zastosowania twierdzenia Pitagorasa do rozwiązywania.

• obliczania wartości funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym.

• wykonywania obliczeń na liczbach rzeczywistych

Wyznaczanie wartości funkcji trygonometrycznych w trójkącie prostokątnym na podstawie ich definicji to elementarna umiejętność z zakresu trygonometrii. Nie było większych problemów z prawidłowym wyznaczeniem wartości funkcji trygonometrycznych kątów α i β. Cieszy również fakt, że większość zdających nie miała problemu z zastosowaniem twierdzenia Pitagorasa do obliczenia długości przeciwprostokątnej. Zdający wykazali się umiejętnością przekształcania wyrażeń trygonometrycznych i obliczali wartość wyrażenia. Ostatnią z ocenianych w zadaniu umiejętności była umiejętność wykonywania działań na ułamkach zwykłych na szczęście dobrze sobie poradzili z podstawowymi działaniami arytmetycznymi na ułamkach i uniknęli błędów rachunkowych.

Najwięcej kłopotów przysporzyło uczniom zadanie 4 i 5.

W zadaniu 4 zdający mieli wykazać się umiejętnościami:

• zapisania w postaci równania lub układu równań zależności między prędkością

i czasem oraz umiejętnościami

• rozwiązania równania kwadratowego i ocenienia przydatności otrzymanych wyników.

Wskaźnik łatwości zadania dla całej Polski wyniósł 0,32 - co oznacza, że zadanie okazało się trudne nie tylko dla naszych maturzystów.

Zapisując zależność między drogą, czasem i prędkością zdający popełniali szereg błędów. Źle zinterpretowali treść zadania, co skutkowało niepoprawnie zapisanymi równaniami. Część zdających po zapisaniu układu równań nie potrafiła go przekształcić do postaci równania kwadratowego. Pojawiały się błędy w wyznaczaniu rozwiązania równania kwadratowego. Niektórzy zdający, wykonując obliczenia, nie zwracali uwagi na stosowane jednostki, dlatego pojawiły się rozwiązania, w których stosowano zamiennie zapisy t = 30 i t = 1/2 w tym samym układzie równań.

Zdający mieli poważne trudności z przeprowadzeniem poprawnej analizy warunków zadania i zbudowaniem modelu matematycznego do przedstawionej sytuacji problemowej. Stąd duża liczba prac, w których maturzyści zakończyli rozwiązywanie problemu na wprowadzeniu oznaczeń, nie zawsze zgodnych z warunkami zadania lub nieudanych próbach zapisania zależności między prędkością, drogą i czasem. Zastosowanie wiadomości i umiejętności matematycznych w „zadaniach praktycznych”, w których nie można wykorzystać gotowych algorytmów jest - jak widać - ogromnym problemem dla wielu zdających.

W zadniu 5 zdający miał wykazać się umiejętnością opisaną w standardzie III.:

• zastosowania własności sum częściowych ciągu arytmetycznego do zapisania wzoru na n-ty wyraz tego ciągu oraz umiejętnością opisaną w standardzie II.:

• wykorzystania własności ciągu arytmetycznego do wyznaczenia wyrazów ciągu określonego w treści zadania.

Wskaźnik łatwości zadania w kraju wyniósł 0,23 - trudne, również u nas to zadanie wypadło bardzo słabo.

Najczęściej popełnianym błędem w pierwszej etapie zadania było mylenie wzoru ogólnego ciągu (a_n) z wzorem ciągu sum częściowych (S_n). Niektórzy zdający do wyznaczenia a_n stosowali błędną zależność. W wielu pracach na skutek wcześniej popełnionych błędów, zdający, rozwiązując równanie a_n = 0, z niewiadomą n, otrzymywali liczbę ujemną lub ułamek i pozostawiali taki wynik bez komentarza. Pojawiały się też błędy rachunkowe, np. przy obliczaniu S₁, S₂, zdający nie uwzględniali znaku minus przed potęgą (kolejność wykonywania działań), oraz popełniali błędy w przekształcaniu wyrażeń algebraicznych. Wielu zdających miało problem z wyznaczeniem pierwszego wyrazu ciągu, ponieważ nie rozumieli zależności a₁=S₁ Zdarzały się, więc rozwiązania, w których zdający wyznaczali n-ty wyraz ciągu, uzależniając go od a₁ i n, a następnie wyznaczali a₂₀₀₇ i liczbę n w zależności od a₁ . Nie można było wówczas ocenić, czy zdający właściwie rozumieją pojęcie ciągu i wskaźnika n-tego wyrazu.

Rozwiązanie zadania wymagało od zdających rozumienia jednego z podstawowych pojęć związanych z ciągiem arytmetycznym - sumy n początkowych wyrazów. Zdający, którzy wyznaczyli wzór na n-ty wyraz ciągu bez trudności i poprawnie rozwiązali pozostałe polecenia. Należy zwrócić uwagę na bardzo niski poziom wykonania pierwszej umiejętności - wykorzystanie własności sum częściowych ciągów: a_n=S_n-S_n-1 oraz a₁=S₁ Zadania związane z ciągiem (arytmetycznym lub geometrycznym) występowały w arkuszach egzaminacyjnych na każdym egzaminie maturalnym i bardzo niepokoi fakt, że sprawiło ono tak wiele kłopotów maturzystom.

Arkusze egzaminacyjne z matematyki zawierały zadania otwarte o zróżnicowanym stopniu trudności. Tematyka zadań w arkuszach obejmowała wszystkie treści Podstawy programowej.

Na podstawie analizy wyników egzaminu maturalnego z matematyki można stwierdzić, że maturzyści:

• Wykazali się umiejętnością budowania modelu matematycznego dla sytuacji opisanej

w zadaniu oraz poprawnego wyboru algorytmu rozwiązania.

• W zadowalającym stopniu wykazali się znajomością podstawowych definicji, twierdzeń

i pojęć związanych z geometrią. Swobodnie posługiwali się twierdzeniem Pitagorasa, twierdzeniem cosinusów oraz własnościami trójkątów i czworokątów.

• Wykazali się znajomością definicji funkcji i ich własności. Dotyczyło to w szczególności funkcji kwadratowej oraz funkcji trygonometrycznych.

• Dobrze wykonywali obliczenia procentowe transakcji kupna i sprzedaży akcji w biurze

maklerskim, wykorzystując informacje ilościowe i jakościowe z tabeli.

• Dobrze opanowali i z powodzeniem stosowali metody rozwiązywania prostych równań

wielomianowych, ale mieli trudności z wykorzystaniem własności ciągów.

Do najsłabiej opanowanych umiejętności należy zaliczyć:

• Przedstawianie toku rozumowania w postaci wyrażenia algebraicznego lub równania.

• Obliczanie prawdopodobieństwa zdarzeń losowych z zastosowaniem twierdzenia

klasyczna definicja prawdopodobieństwa.

• Popełnianie błędów rachunkowych w trakcie przekształcania wyrażeń algebraicznych,

które uniemożliwiały zdającym osiągnięcie poprawnego wyniku.

• Zastosowanie definicji funkcji trygonometrycznych do obliczania pól i objętości figur

geometrycznych.

• Rozwiązywanie zadań z funkcją, w której wystąpiła wartość bezwzględna. Szkicowanie

wykresów i badanie własności tych funkcji sprawiało zdającym kłopoty ze względu

na liczne błędy w trakcie przekształcania wyrażeń algebraicznych.

• Wielu zdających wykazywało brak krytycznego podejścia do otrzymanych wyników,

nie weryfikowało otrzymanych rozwiązań z warunkami zadania.

Większość zdających opanowała umiejętność stosowania prostych algorytmów,

znanych twierdzeń i definicji do rozwiązywania zadań oraz wykonywania obliczeń.

Ci zdający, którzy nie znali typowego algorytmu, prowadzili konsekwentnie rozumowanie, aby znaleźć poprawne rozwiązanie. Można stwierdzić, że zdający poprawnie rozwiązywali typowe problemy o małym stopniu złożoności. W przypadku zadań nietypowych, bardziej złożonych widać, że maturzyści mają problemy już na etapie przeprowadzania analizy zadania.

Czas, który pozostał do majowego egzaminu, maturzyści powinni wykorzystać na rozwiązywanie zadań badających nie tylko umiejętności rozwiązywania problemów, ale również umiejętności korzystania z informacji.

Opracowali:

Danuta Kozakiewicz

Robert Kłoczko

Na podstawie:

- Wyników matury z matematyki w roku szkolnym 2006/2007 w ZS nr 3 w Łukowie.

- Sprawozdania z egzaminu maturalnego 2007.

- Arkuszy egzaminacyjnych.

- Informatora maturalnego.

- Standardów wymagań egzaminacyjnych.

---