Marcin Kornak Wrocław 17 marca 2000

EiT

Nr.indeksu 100927

Temat:

Statystyczna ocena wyników pomiarów.

Pomiary wymiarów liniowych trójkątów.

1.Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie ze statystyczną analizą wyników pomiarów, a w szczególności: sposobami znajdowania i eliminacji wyników pomiarów obarczonych „błędami grubymi”, wyznaczania i analizy składowej przypadkowej oraz składowej systematycznej błędów pomiarów.

2. Program ćwiczenia:

Pomiar trójkąta nr 6 suwmiarką cyfrową o błędzie granicznym ±0,03

3. Tabela wyników dla trójkąta nr 6.

Tabela 1.1. Pomiary boków i wysokości trójkąta nr.3..

Lp.	A [mm]	B [mm]	C [mm]	ha [mm]	hb [mm]	hc [mm]
1.	94,66	83,85	74,72	63,47	71,69	80,39
2.	94,65	83,87	74,75	63,47	72,01	80,38
3.	94,61	83,86	74,70	63,50	71,66	80,41
4.	94,71	83,79	74,74	63,51	71,68	80,37
5.	94,64	83,68	74,72	63,56	71,67	80,54
6.	94,61	83,80	74,71	63,54	71,70	80,41
7.	94,61	83,79	74,73	63,56	71,67	80,40
8.	94,68	83,79	75,73	63,53	71,69	80,37
9.	94,68	83,81	74,71	63,52	71,69	80,39
10.	94,65	83,85	75,75	63,51	71,70	80,36
11.	94,62	83,84	74,71	63,47	71,66	80,34
12.	94,66	83,86	75,75	63,51	71,66	80,36
M^1)	95,197	83,815	74,810	63,512	71,706	80,393
S^2)	0,1940	0 0,0526,00	0,2903	0,0319	0,0967	0,0509

Tabela 1.2. Obliczenia pól trójkąta nr 6.

Lp.	Pa [mm^2]	Pb [mm^2]	Pc [mm^2]	Ph [mm^2]
1.	3004,0	3005,6	3003,4	2996,5
2.	3003,7	3019,7	3004,2	2997,9
3.	3003,9	3004,7	3003,3	2995,4
4.	3007,5	3003,0	3003,4	2996,3
5.	3007,7	2998,7	3009,0	2991,8
6.	3005,8	3004,2	3003,7	2994,2
7.	3009,7	3002,6	3003,1	2994,6
8.	3007,5	3003,5	3043,2	3027,8
9.	3007,0	3004,2	3003,0	2995,4
10.	3005,6	3006,0	3003,5	2997,4
11.	3002,8	3004,0	3001,1	2995,4
12.	3004,7	3004,7	3003,5	2997,8
M^1)	3005,7	3005,1	3007,1	2998,4
S^2)	1,7	5,0	11,5	9,4

4. Sprawdzanie, czy pomiary były obciążone błędami grubymi i ewentualne

przeprowadzenie eliminacji lub korekty tych błędów.

Błędy grube powstają zazwyczaj wskutek pomyłki eksperymentatora (chociaż mogą być spowodowane również nieodpowiednią metodą pomiarową).

W protokole (tabela 1 ; 8 pomiar boku c, oraz 2 pomiar wysokosci hb trójkąta) dostrzegłem dość „podejrzany” wynik. Okazało się, że wynik tego pomiaru wykracza poza przedział, w którym (zgodnie z funkcją Gaussa rozkładu gęstości prawdopodobieństwa) powinno znajdować się 99,7% wyników. Fakt ten sugeruje popełnienie przez studenta 2 i 8 błędu grubego (błędny odczyt z suwmiarki lub pomyłka przy wprowadzaniu danych do pamięci komputera), wobec czego wynik powinien zostać odrzucony podczas analizy pomiarów.

5. Analiza błedow przypadkowych.

Błędami przypadkowymi nazywamy błędy zmieniające się w sposób nieprzewidziany. W chwili pomiaru mierzącemu nie jest znana wartość błędów przypadkowych.

Pomiary bezpośrednie boków i wysokości trójkąta są oczywiście obarczone błędem przypadkowym na co miały wpływ:

• trudności ustawienia mierzonego boku lub wysokości trójkąta prostopadle do szczęk suwmiarki,

• zaokrąglenia wierzchołków trójkąta,

- różnej rozdzielczości oczu mierzących,

• różnych metod pomiaru,

• różnego ścisku suwmiarki stosowanego przez mierzących.

Okazuje się że miary błędów przypadkowych przy pomiarze długości boków są mniejsze od błędów przypadkowych powstałych przy pomiarze wysokości. Wiąże się to ze stosunkowo trudnym ustawieniem mierzonej wysokości trójkąta prostopadle do szczęk suwmiarki. Był to jeden z zasadniczych powodów uzyskiwania różnych długości boków.

6. Analiza błędów systematycznych wyznaczenia powierzchni trójkąta nr 6.

Błędy systematyczne to błędy , które przy wielu pomiarach tej samej wartości wykonywane w tych samych warunkach pozostają stałe lub zmieniają się wg określonego prawa.

Rozmiary obliczonych pól zarówno ze wzoru standardowego jak i wzoru Herona są bardzo do siebie zbliżone. Niemniej jednak pola wyliczona ze wzoru Herona, są mniejsze co do wartości od pól liczonych ze wzoru tradycyjnego. Spowodowane to jest tym że we wzorze Herona wykorzystywane są długości wszystkich trzech boków trójkąta. Pomiary boków ze względu na trudności zmierzenia boku miały tendencję do zaniżania swej wartości.

We wzorze tradycyjnym wykorzystuje się tylko jeden bok i opadająca na niego wysokość. Pomiary wysokości z kolei miały skłonność do zawyżania swej wartości.

Niemniej jednak pola wyliczone ze wzoru Herona ze względu na mniejsze błędy przypadkowe pomiarów boków jest dokładniejszy.

7. Po przeprowadzeniu analizy wyników usunąłem pomiary obarczone grubymi

błędami, zestawienie wyników pomiarów przedstawia poniższa tabelka.

	X	n	S	sx=	Δp=3sx	Δn	δp=	δn=	Ostateczny wynik pomiaru
	mm		mm	mm	mm	mm	%	%	mm
A	94,648	12	0,032	0,009	0,026	0,03	0,028	0,032	94,65 ± 0,06
B	83,815	12	0,053	0,010	0,031	0,03	0,037	0,036	83,82 ± 0,04
C	74,81	12	0,290	------------	-----------	--------------	-------------	--------------	---------------
c'	74,726	11	0,019	0,006	0,017	0,03	0,022	0,040	74,73 ± 0,04
Ha	63,512	12	0,032	0,009	0,028	0,03	0,044		63,51 ± 0,06
Hb	71,706	12	0,097	-------------	-----------	--------------		--------------	---------------
hb'	71,679	11	0,016	0,005	0,014	0,03	0,001	0,042	71,068 ± 0,04
Hc	80,393	12	0,051	0,015	0,044	0,03	0,055	0,037	80,39 ± 0,07
	mm^2		mm^2	mm^2	mm^2	mm^2	%	%	mm^2
Pa	3005,7	12	1,7	0,491	1,472	2,372	0,049	0,079	3005,7 ± 3,8
Pb	3005,1	12	5	-------------	-----------	--------------	-------------	--------------	---------------
Pb'	3003,7	11	1,9	0,573	1,719	2,332	0,057	0,078	3003,7±4,05
Pc	3007,1	12	11,5	-------------	-----------	-------------	-------------	--------------	---------------
Pc'	3003,8	11	1,9	0,573	1,719	2,327	0,057	0,077	3003,8±4,05
Ph	2998,4	12	9,4	-------------	-----------	--------------	-------------	--------------	---------------
Ph'	2995,7	11	1,8	0,543	1,628		0,054		2995,7±

a,b,c - boki trójkąta;

x - średnia arytmetyczna n pomiarów;

s - odchylenie średnie kwadratowe;

s_x - odchylenie średniej arytmetycznej;

Δ_p - błąd przypadkowy graniczny pomiaru ;

Δ_n - błąd graniczny suwmiarki;

δ_p - błąd względny przypadkowy;

δ_n - błąd względny suwmiarki;

1. X - średnia arytmetyczna serii n pomiarów (x₁,x₂,...,x_n ) wielkości fizycznej X wynosi

2. S - Średni błąd kwadratowy pojedynczego pomiaru skończonej serii n pomiarów wielkości fizycznej X wynosi:

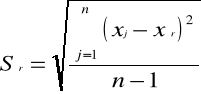
8. Wnioski:

Podczas wykonywania ćwiczenia dwóch studentów popełniło podczas pomiaru jednego z boków i wysokości błąd gruby, który postanowiłem odrzucić. Mogły one zostać popełnione w wyniku nieprawidłowego wpisu do komputera lub pomyłki przy odczycie wartości.

Dokonując obliczeń zauważamy że pomiary boków a,b,c obarczone są mniejszymi błędami niż pomiary odpowiadających im wysokość ha,hb,hc.Wynika to bezpośrednio ze sposobu w jaki zostały wykonane powyższe pomiary. Jak wiadomo wysokość trójkąta jest prostopadła do przeciwległej podstawy a więc aby poprawnie wykonać pomiar należało `przyłożyć' suwmiarke prostopadle do podstawy co mogło sprawiać pewne trudności.

Porównując pola trójkątów wyliczone metodą tradycyjna (a*ha/2) oraz wzorem Herona zauważamy że wyliczenia dokonane wzorem Herona są bardziej dokładne wynika to z faktu iż wzór Herona do obliczenia pola używa wyłącznie długości boków a,b,c które są obarczone mniejszym błędem niż wysokości.

W pomiarach wystąpiły błędy przypadkowe mogły wynikać między innymi z :

- zaokrąglonych wierzchołków trójkątów,

- trudności ustawienia mierzonego boku trójkąta prostopadle do szczęk suwmiarki,

• różnych metod pomiaru (różne ułożenie trójkąta w czasie pomiaru, dociskanie z różną siłą szczęk suwmiarki do mierzonego trójkąta).

Korzystałem ze współczynnika t- studenda, ponieważ pomiarów miałem mniej niż 30.

1

4

Δ_n(P)= Δ_na + Δ_nh = Δ_n [mm²]

---