Wrocław 1998.03.26
Laboratorium
Miernictwa Elektronicznego
Student: DAWID KWIECIEŃ
Wydz. E i T Rok I
Prowadzący: dr inż.R.Jagielnicki
Ćwiczenie Nr 2
TEMAT: Statystyczna analiza wyników pomiarów
I. Cel ćwiczenia
Zapoznanie studenta ze statystyczną analizą wyników pomiarów, a w szczególności : sposobami znajdowania i eliminacji wyników pomiarów obarczonych „błędami grubymi”, wyznaczania i analizy składowej przypadkowej oraz składowej systematycznej błędów pomiarów.
II. Spis przyrządów
1.Suwmiarka elektroniczna o dokładności odczytu 0.01 mm
III. Zadanie
1. Zapoznać się z obsługą suwmiarki i przeprowadzić kilkakrotnie pomiary próbne.
Zmierzyć boki a, b, c oraz wysokości ha, hb, hc trójkąta.
Dokonać pomiaru tych samych wielkości dla pozostałych trójkątów.
Wyniki wprowadzić do komputera.
Przy użyciu programów student.exe, assemble.exe, extract.exe dokonać obróbki otrzymanych wyników.
IV. Tabela zbiorcza wyników pomiarów dla trójkąta Nr 9
Analiza wyników pomiarów i wnioski.
Dokonane pomiary długości boków i wysokości trójkąta nr 9 nie są obarczone błędami
grubymi. Błędy grube powstają przy nieprawidłowym wykonaniu pomiaru np.: uszkodzony przyrząd pomiarowy (suwmiarka), fałszywy odczyt wskazania (np.:1 zamiast 7) itp. Błędy te są błędami o bardzo małym prawdopodobieństwie wystąpienia, a jeśli wystąpią są łatwe w zlokalizowaniu dzięki czemu możliwa jest korekta wyniku pomiaru. Gdy nie możemy dokonać poprawy pomiaru to wyniku obarczonego błędem grubym nie bierzemy pod uwagę.
Błędy przypadkowe to takie, które występują i zmieniają się w sposób nieprzewidziany
zarówno co do wartości bezwzględnej jak i co do znaku, przy wykonywaniu dużej liczby pomiarów tej samej wielkości w warunkach pozornie niezmiennych. Błędy takie wystąpiły co widać w obliczeniach zamieszczonych w tabeli. Powodem wystąpienia ich jest fakt, że pomiaru tej samej wielkości dokonało 12 ćwiczących. Każdy z wykonujących pomiar stosował różne metody ułożenia przedmiotu i suwmiarki oraz precyzyjność pomiaru nie była taka sama u wszystkich. Wartości odchylenia średniego kwadratowego dla poszczególnych boków i wysokości liczone były ze wzoru:
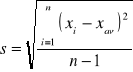
gdzie xav wartość średnia mierzonej wielkości, a xi wartość i-tego pomiaru.
Obserwując wyniki błędów pomiarów dla boków trójkąta widzimy, że są one rzędu 10-2 wielkości rzeczywistej, natomiast wyniki błędów pomiarów dla wysokości trójkąta są rzędu 10-1, co jest dowodem, że zmierzenie wysokości trójkąta przez ćwiczących odbywało się w sposób zróżnicowany, a przez to mniej precyzyjny.
3. Błędy systematyczne wystąpiły w powyższym ćwiczeniu. Możemy zaliczyć je do błędów metody. Łatwo zauważyć je analizując wyniki pól dla trójkąta liczone różnymi metodami. Na większy błąd przy obliczaniu pola zgodnie ze wzorem ![]()
, niż korzystając ze wzoru Herona ![]()
gdzie ![]()
ma wpływ większy błąd wysokości h trójkąta. Wielkość h nie jest wykorzystywana we wzorze Herona, a jest podstawowym czynnikiem wg klasycznego wzoru na pole trójkąta. Gdybyśmy znali niedokładność pomiaru wysokości trójkąta i niedokładność metody obliczeniowej pola trójkąta to moglibyśmy np. przy użyciu poprawki częściowo ten błąd wyeliminować. Całkowita eliminacja błędu systematycznego z wyników pomiarów nie jest możliwa. Pewna ich część zawsze pozostaje w wyniku pomiaru. Ta pozostałość błędu systematycznego, zwana niekiedy błędem resztkowym jest sumowana z błędami przypadkowymi i wpływa na ich rozkład. Możemy stwierdzić, że odpowiedni dobór metody obliczeniowej, właściwości narzędzia pomiarowego, czy sposobu pobierania informacji o wielkości mierzonej wpływa na błąd systematyczny.
2
3
Wyszukiwarka
Podobne podstrony:
C - Statystyczna analiza wyników pomiarów, spraw.
C - Statystyczna analiza wyników pomiarów, statystyczna analiza wynikow pomiarów(miern), Politechnik
C - Statystyczna analiza wyników pomiarów, mier1
C - Statystyczna analiza wyników pomiarów, Lab C c, Cezary Kozłowski
C - Statystyczna analiza wyników pomiarów, Lab C h, Pomiar
C - Statystyczna analiza wyników pomiarów, SP, Kozieł Piotr
C - Statystyczna analiza wyników pomiarów, KOREK, Marcin Kornak
C - Statystyczna analiza wyników pomiarów, miernictwo3-Marek, SPRAWOZDANIE
C - Statystyczna analiza wyników pomiarów, spr trˇj, x
C Statystyczna analiza wyników pomiarów lab z mier
C - Statystyczna analiza wyników pomiarów, m-2, Wykona˙ : Grzegorz Kozik
C - Statystyczna analiza wyników pomiarów, Lab C e, Laboratorium miernictwa elektronicznego
C - Statystyczna analiza wyników pomiarów, cw 1, Protokół z ćwiczenia: Statystyczna analiza wyników
Statystyczna analiza wyników pomiarów, Sprawolki
C - Statystyczna analiza wyników pomiarów, Lab C i, Sprawozdanie
C - Statystyczna analiza wyników pomiarów, Statystyczna analiza wyników pomiarów, Statystyczna anali
Statystyczna analiza wyników pomiarów, Informatyka, Podstawy miernictwa, Laboratorium
C - Statystyczna analiza wyników pomiarów, Lab C g, Laboratorium Miernictwa Elektronicznego
C - Statystyczna analiza wyników pomiarów, CW3MIERN, Zespół Szkół Elektronicznych
więcej podobnych podstron