Nr ćwicz. 102	Data 20.03.03	Paweł Matuszak	wydział elektryczny	Semestr II	E9 1
mgr Janusz Rzeszutek		przygotowanie:	wykonanie:	ocena:

Wyznaczanie modułu sztywności metodą dynamiczną

Do wyznaczania modułu sztywności metodą dynamiczną używamy cienkiego pręta lub drutu, przymocowanego górnym końcem do uchwytu. Na dolnym końcu zawieszony jest wibrator, zbudowany z dwóch skrzyżowanych prętów z kołkami umożliwiającymi zakładanie dodatkowych obciążeń.

Gdy wibrator zostanie skręcony o pewien kąt, w drucie wystąpi moment sił sprężystości, w skutek których wibrator będzie się poruszał ruchem harmonicznym o okresie:

gdzie I₀ - moment bezwładności; D - moment kierujący

Moment kierujący obliczamy z równania:

(*) gdzie l - długość drutu; r - promień drutu

Aby wyeliminować nieznany moment bezwładności nieobciążonego wibratora zauważamy, że po obciążeniu wibratora dodatkową masą jego moment bezwładności zwiększy się o I₁, a okres drgań będzie wynosił:

Po podstawieniu otrzymujemy:

Porównując powyższe równanie z (*) otrzymujemy:

Przy czym I₁ dla k ciężarków uzyskujemy ze wzoru

gdzie m_k - masa ciężarka k; d_k - odległość osi ciężarka k od osi wibratora

I_k jest momentem bezwładności pojedynczego ciężarka k, i dla walca wynosi:

gdzie R - promień walca

Stąd, dla dwóch równo oddalonych ciężarków otrzymujemy wzór:

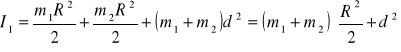
Pomiary i obliczenia

Mierzymy długość drutu l:

l = 1,642 [m] ∆l=0,001 [m]

Następnie dokonujemy 10 pomiarów średnicy drutu x = 2r:

L.p.	x=2r [mm]
1	1,00
2	1,00
3	1,00
4	1,05
5	1,00
6	1,00
7	1,00
8	1,05
9	1,00
10	1,00

Pomiary nr 4 i nr 8 różnią się o 0,05 mm, tj. o wartość błędu systematycznego wynikającego z dokładności odczytu. Dlatego też możemy przyjąć x = 1,00 mm i nie stosować teorii błędów przypadkowych dla tego pomiaru.

0,50 [mm] = 0,0005 [m]

∆x = 0,05 [mm] = 0,00005 [m]

[m]

Wyznaczamy masę oraz średnicę i promień ciężarków:

m₁ = 94,19 [g] = 0,09419 [kg]

m₂ = 91,28 [g] = 0,09128 [kg]

∆m = 0,01 [g] = 0,00001 [kg]

X = 2R = 32,2 [mm] = 0,0322 [m]

∆X = 0,05 [mm] = 0,00005 [m]

[m]

[m]

Mierzymy odległości kołków wibratora od jego środka:

d₁ = 0,05015 [m]

d₂ = 0,1014 [m]

d₃ = 0,15 [m]

∆d = 0,00005 [m]

Liczymy momenty bezwładności poszczególnych układów wraz z błędem według wzoru:

położenie ciężarków [m]	I	∆I
d1 = 0,05015	0,0004905	0,0000011
d2 = 0,1014	0,0019313	0,0000026
d3 = 0,15	0,0041971	0,0000034

Następnie mierzymy czas 10 okresów drgań dla obciążenia wstępnego i ciężarków umieszczonych kolejno w położeniach d₁ d₂ d₃ oraz liczymy okres średni i odchylenie standardowe średniej arytmetycznej według wzorów:

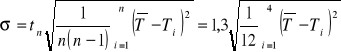
przyjmując
[s] oraz współczynnik Studenta - Fishera dla 4 prób t_n = 1,3

Obciążenie wstępne:

Numer próby	t = 10 T0 [s]	T0= t / 10 [s]
1	46,00	4,6
2	46,00	4,6
3	45,91	4,591
4	45,90	4,59

= 4,59525 ≈ 4,5953 [s]

σ₀ = 0,003575 ≈ 0,0036 [s]

poł. ciężarków w d₁ = 0,05015 [m]:

Numer próby	t = 10 T1 [s]	T1= t / 10 [s]
1	50,16	5,016
2	49,90	4,99
3	49,91	4,991
4	49,97	4,997

= 4,9985 ≈ 4,999 [s]

σ₁ = 0,007845 ≈ 0,008 [s]

poł. ciężarków w d₂ = 0,1014 [m]:

Numer próby	t = 10 T2 [s]	T2= t / 10 [s]
1	60,13	6,013
2	60,31	6,031
3	60,12	6,012
4	60,33	6,033

= 6,02225 ≈ 6,022 [s]

σ₂ = 0,007342 ≈ 0,008 [s]

poł. ciężarków w d₃ = 0,15 [m]:

Numer próby	t = 10 T3 [s]	T3= t / 10 [s]
1	73,72	7,372
2	74,15	7,415
3	73,59	7,359
4	73,78	7,378

= 7,381 [s]

σ₃ = 0,01561 ≈ 0,016 [s]

Liczymy moduły skręcania dla poszczególnych przypadków i ich błędy:

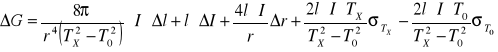
położenie ciężarków [m]	G [Nm^-1 rad^-1]	∆G [Nm^-1 rad^-1]
d1 = 0,05015	8,04 * 10^10	1,80 * 10^10
d2 = 0,1014	8,09 * 10^10	1,74 * 10^10
d3 = 0,15	7,98 * 10^10	1,73 * 10^10

Średni moduł sprężystości:

= 8,0356 *10¹⁰ ≈ 8,04 *10¹⁰ [Nm^-1rad^-1]

Odchylenie standardowe średniej arytmetycznej modułu sprężystości:

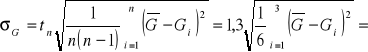
0,03989 *10¹⁰ ≈ 0,04 *10¹⁰ [Nm^-1rad^-1]

Średni błąd modułu sprężystości:

= 1,7566 *10¹⁰ ≈ 1,76 *10¹⁰ [Nm^-1rad^-1]

Odchylenie standardowe średniej arytmetycznej błędu modułu sprężystości:

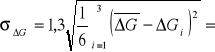
0,01177 *10¹⁰ ≈ 0,029 *10¹⁰ [Nm^-1rad^-1]

Ostatecznie: G = ( 8,04 ±1,76 ) *10¹⁰ [Nm^-1rad^-1]

Moduł sprężystości stali odczytany z tablic: G = 8,15 *10¹⁰ [Nm^-1rad^-1]

Wnioski

Dokonany pomiar jest zgodny z odczytem z tablic fizycznych.

Wysoka wartość błędu spowodowana jest w głównej mierze tym, że stosunek błędu pomiaru promienia przekroju druta do wyliczonego średniego promienia jest duży. Uwidacznia się to w szczególności, iż we wzorze na moduł sztywności używamy wartości promienia podniesionej do czwartej potęgi, co powoduje wzrost wagi tego błędu.

---