Nr ćwicz. 301	Data	Paweł Matuszak	wydział elektryczny	Semestr II	E9 1
mgr Janusz Rzeszutek		przygotowanie:	wykonanie:	ocena:

Wyznaczanie współczynnika załamania światła

metodą najmniejszego odchylenia w pryzmacie

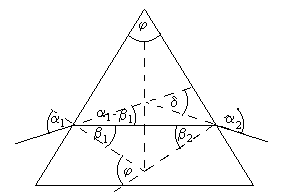
Promień światła napotykając na granicę pomiędzy dwoma ośrodkami przy przejściu z jednego ośrodka do drugiego ulega załamaniu. Kąt padania α to kąt zawarty między prostopadłą do obydwu ośrodków a promieniem padającym P. Kąt załamania β, to kąt zawarty między prostopadłą a promieniem przepuszczonym. Załamanie światła na powierzchni rozgraniczającej dwa ośrodki opisane jest prawem Snella.

Prawa Snella w postaci powyższej nie używa się do praktycznego wyznaczania współczynnika załamania ze względu na niedogodność i niedokładność wyznaczania kątów padania i załamania, natomiast możemy je skutecznie zastosować do pryzmatu, gdzie kąty α i β można wyrazić przez inne, dogodne do pomiaru wielkości.

W ćwiczeniu wykorzystujemy tylko dwie płaszczyzny pryzmatu, tworzące między sobą kąt ϕ, zwany kątem łamiącym. Promień świetlny padający na pryzmat ulega dwukrotnemu załamaniu i zostaje odchylony o pewien kąt ϕ, zależny od kąta padania α oraz kąta od kąta łamiącego ϕ. Na podstawie rysunku możemy wyrazić kąt odchylenia następująco:

Kąt padania możemy tak dobrać, aby promień biegnący wewnątrz pryzmatu był prostopadły do dwusiecznej kąta łamiącego ϕ. W tej sytuacji bieg promienia jest symetryczny, tzn. α₁=α₂ oraz β₁=β₂, a kąt odchylenia - najmniejszy z możliwych dla danego pryzmatu. Zauważając, że 2β=ϕ, możemy przekształcić równanie do postaci:

Podstawiając wyrażone powyżej wartości α i β do wzoru definiującego współczynnik załamania, otrzymamy:

Stosując powyższy wzór możemy wyznaczyć n na podstawie pomiarów kąta łamiącego i kąta najmniejszego odchylenia.

Obliczenia --> [Author:MF]

Dokonuję pomiaru kąta łamiącego. Ustawiam pryzmat tak, by dwusieczna kąta łamiącego była równoległa do padającej wiązki światła i mierzę jej odchylenie w lewo i prawo.

α_P = 58⁰23' α_L = 13⁰27' α₀ = 99⁰21' Obliczam wartość kąta ϕ i jego błędu z równania:

= 22⁰28'

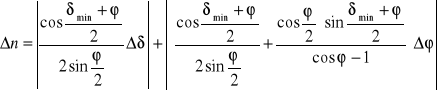
śwatło	λ [nm]	αL [^0]	αP [^0]	δmin [^0]	n	Δn
czerwone ciemne	675	105^000'	75^044'	14^038'	1,6331	0,0019
czerwone jasne	656	105^003'	75^039'	14^042'	1,6359	0,0019
pomarańczowe	600	105^006'	75^036'	14^045'	1,6380	0,0019
żółte	589	105^007'	75^037'	14^045'	1,6380	0,0019
zielone	554	105^009'	75^036'	14^046'30''	1,6391	0,0019
niebieskie	500	105^014'	75^035'	14^049'30''	1,6412	0,0019
fioletowe	439	105^024'	75^023'	15^000'30''	1,6490	0,0019

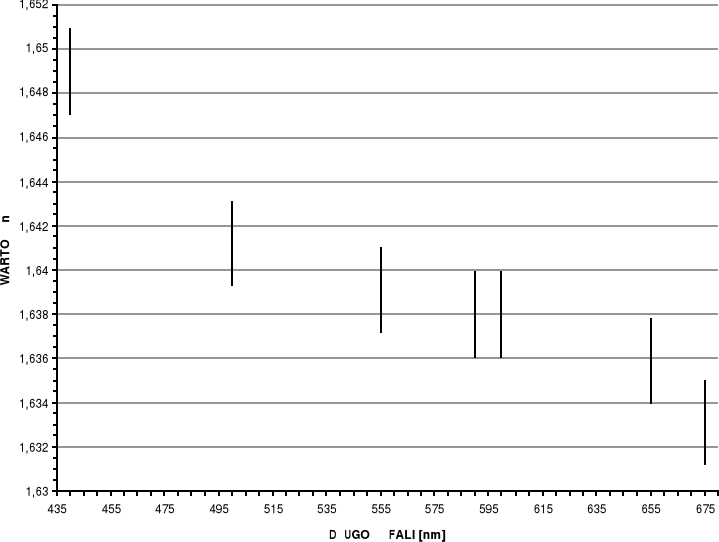
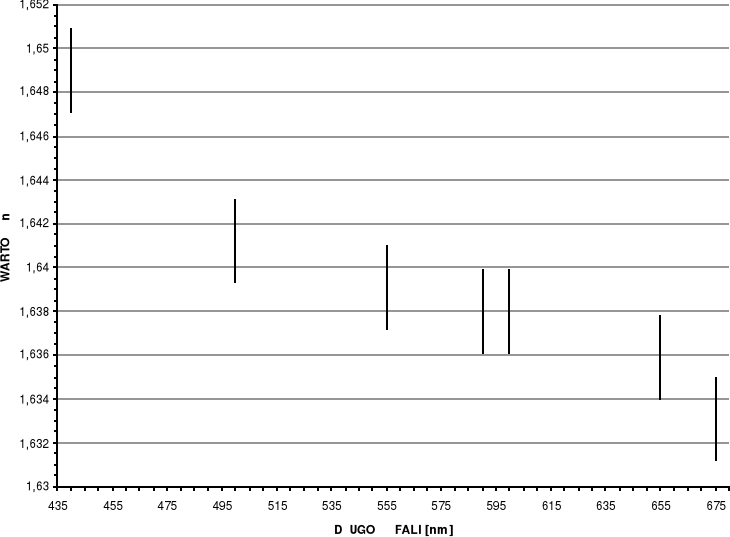
Wykres zależności n=f(λ)

Wnioski

Na wykresie krzywej dyspersji n = f(λ) prostokąty błędu są tak duże, gdyż wynika to z przyjętej skali i niewielkiej różnicy między wartościami n w stosunku do obliczonego błędu. Niemniej jednak wykres krzywej dyspersji przebiega prawidłowo tzn. im większa długość fali tym mniejsze złamanie. Można wnioskować, że ćwiczenie zostało wykonane poprawnie.

---