Przykłady rozwinięć funkcji w szeregi potęgowe dla :

, (1.34)

, (1.35)

- sinus całkowy

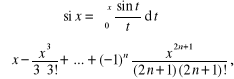
(1.36)

- całka Laplace'a

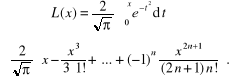
(1.37)

Chociaż szeregi (1.34) ÷ (1.37) są zbieżne dla dowolnych wartości x, jednak dostatecznie dobre przybliżenia można uzyskać jedynie dla argumentów x dostatecznie bliskich zeru. Dla dużych wartości argumentów x trzeba bowiem zsumować dużą liczbę wyrazów, często o dużych wartościach bezwzględnych i o różnych znakach - co, zgodnie z oszacowaniem (1.5), może spowodować znaczne zmniejszenie dokładności obliczeń np.: wartość sinusa 2550° obliczona w podwójnej precyzji za pomocą szeregu (1.35) wynosi 29.5 [5]. Stąd też funkcje standardowe są wyznaczane przez kompilatory języków programowania przy wykorzystaniu bardziej efektywnych algorytmów numerycznych.

Optymalne algorytmy obliczania wartości szeregów potęgowych (1.34) ÷ (1.37) można uzyskać wyznaczając zależności rekurencyjne między kolejnymi wyrazami tych szeregów:

- funkcja

( k = 1, 2, ...), (1.38)

- funkcja sin x

( k = 1, 2, ...), (1.39)

- funkcja si x

( k = 1, 2, ...), (1.40)

- funkcja

( k = 1, 2, ...). (1.41)

Przerwanie operacji sumowania wyrazów następuje wówczas, gdy

{Program 1.4}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons, OleCtnrs;

. . . . . . . . . . . . . . . . . . . . . .

var

Form3: TForm3;

i,k,k1,n: Integer;

a,blad,dx,eps,sum,x,xmax: Real;

nap,zbior: String;

plik: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

zbior:=Edit4.Text;

AssignFile(plik,zbior); Rewrite(plik);

if RadioButton1.Checked then nap:='Exp(x)' else nap:='Sin(th)';

Writeln(plik,'PROGRAM 1.4.');

Writeln(plik,'Obliczanie wartości funkcji ',nap,'.');

Writeln(plik,'Metoda sumowania szeregów potęgowych.');

n:=StrToInt(Edit1.Text);

Write(plik,'n = ',n:3);

xmax:=StrtoFloat(Edit2.Text);

if RadioButton1.Checked then

Write(plik,', xmax = ',xmax:13)

else

Write(plik,', thmax = ',xmax:13);

eps:=StrToFloat(Edit3.Text);

Writeln(plik,', eps = ',eps:9);

Writeln(plik,'');

if RadioButton1.Checked then

Writeln(plik,' i x ',nap,' błąd')

else

Writeln(plik,' i th ',nap,' błąd');

if RadioButton2.Checked then xmax:=xmax*Pi/180;

dx:=xmax/n;

for i:=1 to n do begin

x:=i*dx; k:=0;

if RadioButton1.Checked then a:=1 else a:=x;

sum:=a;

while Abs(a)>eps do begin

k:=k+1;

if RadioButton2.Checked then k1:=2*k;

if RadioButton1.Checked then a:=x*a/k

else a:=-Sqr(x)*a/k1/(k1+1);

sum:=sum+a;

end;

if RadioButton1.Checked then blad:=Abs(sum-Exp(x))

else blad:=Abs(sum-Sin(x));

if RadioButton2.Checked then x:=x*180/Pi;

Writeln(plik,i:3,' ',x:7:4,' ',sum:18,' ',blad:11);

end;

CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(zbior);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

Zadaniem programu 1.4 jest obliczanie z dokładnością wartości funkcji oraz funkcji sin x przy wykorzystaniu wzorów (1.38) i (1.39) w zadanych przedziałach
w n równoodległych punktach oraz porównanie tych wyników z wynikami uzyskanymi za pomocą funkcji standardowych. Rezultaty przykładowych obliczeń numerycznych - zapisywanych w pliku Pr_1_4.wyn - przedstawiają się następująco:

PROGRAM 1.4.

Obliczanie wartości funkcji Exp(x).

Metoda sumowania szeregów potęgowych.

n = 100, xmax = 1.0000E+0001, eps = 1.0E-0008

i x Exp(x) błąd

1 0.1000 1.105170918E+0000 2.01E-0011

2 0.2000 1.221402758E+0000 6.26E-0011

3 0.3000 1.349858808E+0000 5.45E-0011

4 0.4000 1.491824698E+0000 3.11E-0011

5 0.5000 1.648721270E+0000 2.81E-0010

6 0.6000 1.822118800E+0000 9.40E-0011

7 0.7000 2.013752707E+0000 5.25E-0010

8 0.8000 2.225540928E+0000 1.50E-0010

9 0.9000 2.459603111E+0000 6.30E-0010

10 1.0000 2.718281828E+0000 1.70E-0010

11 1.1000 3.004166023E+0000 6.04E-0010

12 1.2000 3.320116923E+0000 1.59E-0010

13 1.3000 3.669296667E+0000 4.94E-0010

14 1.4000 4.055199967E+0000 1.28E-0010

15 1.5000 4.481689070E+0000 3.65E-0010

16 1.6000 4.953032423E+0000 9.75E-0010

17 1.7000 5.473947391E+0000 2.35E-0010

18 1.8000 6.049647464E+0000 6.50E-0010

19 1.9000 6.685894442E+0000 1.59E-0010

20 2.0000 7.389056099E+0000 4.07E-0010

21 2.1000 8.166169912E+0000 9.48E-0010

22 2.2000 9.025013499E+0000 2.46E-0010

23 2.3000 9.974182454E+0000 5.64E-0010

24 2.4000 1.102317637E+0001 1.25E-0009

25 2.5000 1.218249396E+0001 3.35E-0010

26 2.6000 1.346373803E+0001 7.12E-0010

27 2.7000 1.487973172E+0001 1.47E-0009

28 2.8000 1.644464677E+0001 4.27E-0010

29 2.9000 1.817414537E+0001 8.14E-0010

30 3.0000 2.008553692E+0001 1.67E-0009

31 3.1000 2.219795128E+0001 4.25E-0010

32 3.2000 2.453253020E+0001 8.83E-0010

33 3.3000 2.711263892E+0001 1.75E-0009

34 3.4000 2.996410005E+0001 5.42E-0010

35 3.5000 3.311545196E+0001 9.53E-0010

36 3.6000 3.659823444E+0001 1.75E-0009

37 3.7000 4.044730436E+0001 4.60E-0010

38 3.8000 4.470118449E+0001 1.05E-0009

39 3.9000 4.940244910E+0001 1.89E-0009

40 4.0000 5.459815003E+0001 3.97E-0010

41 4.1000 6.034028760E+0001 8.79E-0010

42 4.2000 6.668633104E+0001 2.04E-0009

43 4.3000 7.369979370E+0001 7.29E-0010

44 4.4000 8.145086866E+0001 1.01E-0009

45 4.5000 9.001713130E+0001 1.74E-0009

46 4.6000 9.948431564E+0001 4.48E-0010

47 4.7000 1.099471724E+0002 7.23E-0010

48 4.8000 1.215104175E+0002 1.58E-0009

49 4.9000 1.342897797E+0002 3.92E-0010

50 5.0000 1.484131591E+0002 6.08E-0010

51 5.1000 1.640219073E+0002 1.53E-0009

52 5.2000 1.812722419E+0002 4.13E-0010

53 5.3000 2.003368100E+0002 7.45E-0010

54 5.4000 2.214064162E+0002 1.85E-0009

55 5.5000 2.446919323E+0002 1.83E-0009

56 5.6000 2.704264074E+0002 1.96E-0009

57 5.7000 2.988674010E+0002 3.83E-0010

58 5.8000 3.302995599E+0002 2.16E-0009

59 5.9000 3.650374679E+0002 5.87E-0010

60 6.0000 4.034287935E+0002 4.74E-0010

61 6.1000 4.458577701E+0002 2.12E-0009

62 6.2000 4.927490411E+0002 4.97E-0010

63 6.3000 5.445719101E+0002 4.48E-0010

64 6.4000 6.018450379E+0002 1.92E-0009

65 6.5000 6.651416330E+0002 4.09E-0009

66 6.6000 7.350951892E+0002 1.42E-0010

67 6.7000 8.124058252E+0002 1.33E-0009

68 6.8000 8.978472917E+0002 2.78E-0009

69 6.9000 9.922747156E+0002 2.45E-0009

70 7.0000 1.096633158E+0003 1.36E-0010

71 7.1000 1.211967074E+0003 2.71E-0010

72 7.2000 1.339430764E+0003 2.93E-0009

73 7.3000 1.480299928E+0003 1.56E-0009

74 7.4000 1.635984430E+0003 1.61E-0011

75 7.5000 1.808042414E+0003 5.05E-0009

76 7.6000 1.998195895E+0003 1.19E-0009

77 7.7000 2.208347992E+0003 1.29E-0008

78 7.8000 2.440601978E+0003 7.60E-0009

79 7.9000 2.697282328E+0003 9.12E-0009

80 8.0000 2.980957987E+0003 9.73E-0009

81 8.1000 3.294468075E+0003 5.24E-0009

82 8.2000 3.640950307E+0003 6.50E-0009

83 8.3000 4.023872394E+0003 2.41E-0009

84 8.4000 4.447066748E+0003 1.22E-0009

85 8.5000 4.914768840E+0003 1.07E-0009

86 8.6000 5.431659591E+0003 1.03E-0008

87 8.7000 6.002912217E+0003 1.59E-0008

88 8.8000 6.634244006E+0003 1.28E-0009

89 8.9000 7.331973539E+0003 2.41E-0008

90 9.0000 8.103083928E+0003 3.61E-0009

91 9.1000 8.955292704E+0003 2.53E-0008

92 9.2000 9.897129059E+0003 1.13E-0008

93 9.3000 1.093801920E+0004 1.07E-0008

94 9.4000 1.208838073E+0004 6.49E-0009

95 9.5000 1.335972683E+0004 1.04E-0009

96 9.6000 1.476478156E+0004 1.79E-0008

97 9.7000 1.631760720E+0004 6.18E-0008

98 9.8000 1.803374493E+0004 6.18E-0008

99 9.9000 1.993037044E+0004 2.24E-0008

100 10.0000 2.202646579E+0004 5.00E-0009

PROGRAM 1.4.

Obliczanie wartości funkcji Sin(th).

Metoda sumowania szeregów potęgowych.

n = 45, thmax = 9.0000E+0001, eps = 1.0E-0008

i th Sin(th) błąd

1 2.0000 3.489949670E-0002 5.87E-0014

2 4.0000 6.975647374E-0002 7.08E-0014

3 6.0000 1.045284632E-0001 4.08E-0014

4 8.0000 1.391731010E-0001 6.03E-0015

5 10.0000 1.736481777E-0001 3.35E-0013

6 12.0000 2.079116908E-0001 2.14E-0012

7 14.0000 2.419218956E-0001 1.88E-0013

34 1. Wprowadzenie do metod numerycznych

1.7. Sumowanie szeregów potęgowych 33

---