Ćw. M4 |
Lipiński Zbigniew
|
WMiBM |
||
Gr.14A |
Tablica Galtona. Mechaniczny model rozkładu normalnego. |
|||
|
Ocena |
Data |
Podpis |
|
|
|
|
|
|
Wprowadzenie
Tablica Galtona składa się z wielu rzędów kołeczków umieszczonych nad przegródkami. Na ów układ kołeczków sypiemy kuleczki z lejka, poszczególne kuleczki ulegają zderzeniom z kołeczkami, wpadając ostatecznie do przegródek.
Z tablicą Galtona wiąże się pojęcie odchylenia standardowego oraz teoria niepewności przypadkowych. Rozważania ograniczymy do pomiarów bezpośrednich, w których niepewności systematyczne są bardzo małe w stosunku do niepewności przypadkowych. Próba, czyli seria wyników x1, x2, x3,...,xn, obarczonych pewną niepewnością przypadkową, wyróżnia się tym, że największy z przyczynków niepewności systematycznej Δx jest bardzo mały w porównaniu z różnicą wyników skrajnych: maksymalnego xM i minimalnego xm: Δx << xM - xm.
Prawidłowości występujące w wynikach pomiarowych, wykazujących rozrzut statyczny omówimy na przykładzie próby dużej n = 100. W próbie takiej, niektóre wyniki powtarzają się. Oznaczmy przez x1, x2,..., xk, xK różniące się wyniki xi, uporządkowane w szereg rosnący (wskaźniki i = 1, 2, 3,..., n oznaczają numer kolejny wyniku, k - numer wyniku xk, różnego od innych, K - liczbę wyników xi. ) Liczbę wyników dających wartość xk oznaczamy przez nk. Oczywiście musi zachodzić związek:
∑ Nk = N
k=1
Uporządkowane w ten sposób wyniki można przedstawić graficznie na histogramie. Na osi odciętych nanosi się przedziały klasowe - prawostronnie domknięte przedziały liczbowe, a na osi rzędnych liczebność nk lub liczebności względne nk / n. Histogram stanowi więc zbiór prostokątów o podstawie równej szerokości przedziału klasowego i wysokości równej liczebności nk klasy. Histogram pozwala łatwiej zauważyć prawidłowości występujące w serii wyników pomiarowych. Pewne wartości pojawiają się częściej, a inne, bardzo małe lub bardzo duże, występują rzadko. Dla każdej serii wyników pomiarowych, wykonanych dla tego samego obiektu, histogram przebiega nieco inaczej, lecz ogólne prawidłowości występują zawsze, dzięki czemu każdą próbę można przybliżyć za pomocą jednej, wspólnej krzywej, zwanej krzywą Gaussa lub krzywą gęstości rozkładu normalnego opisaną równaniem:
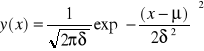
W wyrażeniu tym występują dwa parametry μ i δ, charakteryzujące mierzony obiekt: wartość oczekiwaną, będącą liczbą określającą położenie max. krzywej, odchylenie standardowe, charakteryzujące jej szerokość, czyli odchylenie wyników. Wielkość y(x) jest gęstością prawdopodobieństwa wyników pomiarowych..
Pomiary
Zestaw przyrządów:
tablica Galtona,
zestaw kulek
Opis doświadczenia:
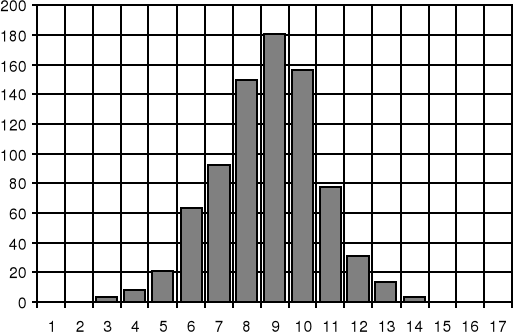
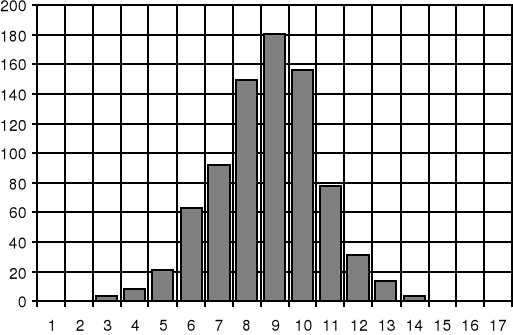
Wykonaliśmy 800 pomiarów, następnie uporządkowaliśmy wyniki pomiarów, grupując razem wyniki jednakowe. Z pomiarów otrzymaliśmy serię 800 wyników, które podzieliliśmy na 17 grup.
Przypuszczamy, że rozkład ten jest rozkładem normalnym. W celu znalezienia wartości średniej x i średniego błędu kwadratowego Sx, wygodniej jest zapisać wynik w postaci tabeli typu I.
Na podstawie tabeli I sporządziliśmy tabelę II. Następnie znormalizowaliśmy rozkład doświadczalny za pomocą podstawienia: Ui = xi - x / Sx.
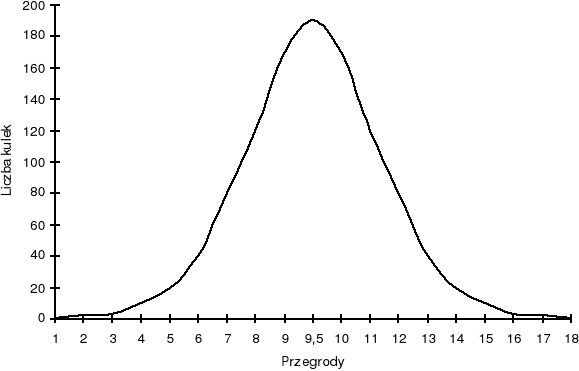
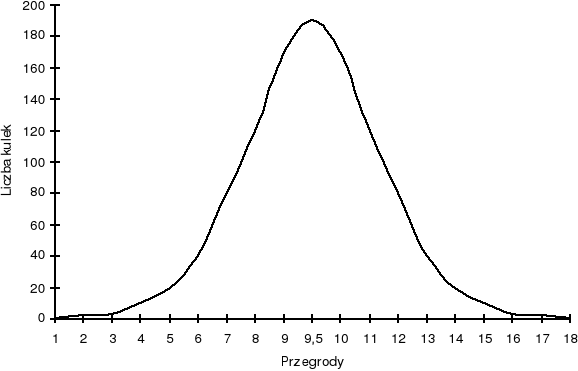
Na histogram wyników nanieśliśmy krzywą teoretyczną, co pozwoliło nam ocenić w przybliżeniu charakter rozkładu. Zwykle ocena taka nie jest wystarczająca i wówczas korzystamy z testu λ2 . W tym celu „zsypaliśmy'' końcowe grupy, tak, aby spełniony był warunek ni > 5. Ilość grup po tej operacji wynosiła m = 10, czyli ilość stopni swobody k = m-r (gdzie r oznacza liczbę parametrów rozkładu teoretycznego oraz dodatkowych, określających go warunków.) W tym przypadku k = 10-3 =7. Dla k=7 oraz znalezionej wartości X2, znajdujemy w tablicy V odpowiadające im prawdopodobieństwo P. Jeśli wartość prawdopodobieństwa P odczytana z tablicy przewyższa 0.01, to rozkład doświadczalny uznajemy za normalny.
Opracowanie wyników
TABELA NR 1
Xi |
Numer pomiaru [Ni] |
||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Suma |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
3 |
4 |
1 |
0 |
0 |
2 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
8 |
5 |
0 |
2 |
0 |
1 |
0 |
2 |
1 |
3 |
1 |
2 |
1 |
0 |
1 |
4 |
0 |
3 |
21 |
6 |
4 |
2 |
4 |
4 |
6 |
7 |
3 |
5 |
2 |
5 |
4 |
2 |
3 |
5 |
6 |
1 |
63 |
7 |
4 |
5 |
7 |
4 |
9 |
6 |
7 |
5 |
4 |
6 |
3 |
7 |
4 |
3 |
7 |
11 |
92 |
8 |
12 |
7 |
12 |
11 |
5 |
9 |
10 |
8 |
15 |
11 |
8 |
11 |
8 |
13 |
4 |
6 |
150 |
9 |
17 |
8 |
12 |
7 |
13 |
9 |
8 |
9 |
11 |
11 |
12 |
12 |
14 |
11 |
13 |
14 |
181 |
10 |
11 |
10 |
8 |
11 |
9 |
5 |
11 |
14 |
11 |
3 |
12 |
10 |
12 |
6 |
14 |
9 |
156 |
11 |
8 |
4 |
6 |
5 |
5 |
6 |
5 |
4 |
2 |
10 |
3 |
7 |
5 |
4 |
1 |
3 |
78 |
12 |
2 |
0 |
1 |
3 |
3 |
2 |
3 |
0 |
3 |
0 |
3 |
1 |
3 |
2 |
2 |
3 |
31 |
13 |
2 |
0 |
0 |
1 |
2 |
2 |
0 |
0 |
1 |
2 |
1 |
0 |
0 |
1 |
2 |
0 |
14 |
14 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
16 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
17 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
TABELA NR 2
Xi |
Ni |
Ni Xi |
/Xi - X'/ |
/Xi - X'/2 |
Ni/Xi - X'/2 |
1 |
0 |
0 |
7,7525 |
60,1012 |
0 |
2 |
0 |
0 |
6,7525 |
45,5962 |
0 |
3 |
3 |
9 |
5,7525 |
33,0912 |
99,2737 |
4 |
8 |
32 |
4,7525 |
22,5862 |
180,69 |
5 |
21 |
105 |
3,7525 |
14,0812 |
295,7063 |
6 |
63 |
378 |
2,7525 |
7,5762 |
477,3041 |
7 |
92 |
644 |
1,7525 |
3,0712 |
282,5555 |
8 |
150 |
1200 |
0,7525 |
0,5662 |
84,9384 |
9 |
181 |
1629 |
0,2475 |
0,0612 |
11,0873 |
10 |
156 |
1560 |
1,2475 |
1,5562 |
242,7759 |
11 |
78 |
858 |
2,2475 |
5,0512 |
393,9979 |
12 |
31 |
372 |
3,2475 |
10,5462 |
326,9339 |
13 |
14 |
182 |
4,2475 |
18,0412 |
252,5775 |
14 |
3 |
42 |
5,2475 |
27,5362 |
82,6087 |
15 |
0 |
0 |
6,2475 |
39,0312 |
0 |
16 |
0 |
0 |
7,2475 |
52,5262 |
0 |
17 |
0 |
0 |
8,2475 |
68,0212 |
0 |
suma |
800 |
7002 |
|
|
2730,45 |
Gdzie: Xi - kolejne przegrody,
Ni - ilość wszystkich kulek w i - tej przegrodzie,
X' - wartość średnia.
TABELA NR 3
Xi |
Ni |
Ui=/Xi-X'//Sx |
P/Ui/ |
Ni'=(P/Ui/)/Sx |
/Ni - Ni'/ |
/Ni - Ni'/ |
/Ni - Ni'//Ni |
1 |
0 |
4,1937 |
0,00005 |
0,0216 |
0,0216 |
0,0005 |
0 |
2 |
0 |
3,6527 |
0,00049 |
0,2120 |
0,2120 |
0,0450 |
0 |
3 |
3 |
3,1118 |
0,00316 |
1,3675 |
1,6324 |
2,6650 |
0,8883 |
4 |
8 |
2,5708 |
0,01431 |
6,1927 |
1,8072 |
3,2660 |
0,4082 |
5 |
21 |
2,0299 |
0,0508 |
21,9842 |
0,9842 |
0,9687 |
0,0461 |
6 |
63 |
1,4889 |
0,1315 |
56,9079 |
6,0920 |
37,1133 |
0,5891 |
7 |
92 |
0,9480 |
0,2541 |
109,9642 |
17,9642 |
322,7160 |
3,5077 |
8 |
150 |
0,4070 |
0,368 |
159,2556 |
9,2556 |
85,6671 |
0,5711 |
9 |
181 |
0,1338 |
0,3956 |
171,1998 |
9,8001 |
96,0434 |
0,5306 |
10 |
156 |
0,6748 |
0,3187 |
137,9205 |
18,0794 |
326,8651 |
2,0952 |
11 |
78 |
1,2157 |
0,189 |
81,7916 |
3,7916 |
14,3764 |
0,1843 |
12 |
31 |
1,7567 |
0,0848 |
36,6980 |
5,6980 |
32,4677 |
1,0473 |
13 |
14 |
2,2976 |
0,0283 |
12,2471 |
1,7528 |
3,0726 |
0,2194 |
14 |
3 |
2,8386 |
0,0069 |
2,9860 |
0,0139 |
0,0002 |
6,4928E-05 |
15 |
0 |
3,3795 |
0,00127 |
0,5496 |
0,5496 |
0,3021 |
0 |
16 |
0 |
3,9205 |
0,00017 |
0,0735 |
0,0735 |
0,0054 |
0 |
17 |
0 |
4,4614 |
0,000017 |
0,0073 |
0,0073 |
0,0001 |
0 |
x' = ( ∑Ni*Xi)/( ∑Ni)
czyli x' = 8,7525
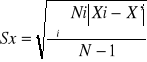
czyli Sx = 1,8486
Ui = |Xi - X'| / Sx
Gdzie: Sx - średni błąd kwadratowy pojedynczego pomiaru
N - całkowita liczba pomiarów
Ui - parametr rozkładu
Kryterium Λ2 :
Λ2 = ∑(Ni - Ni')2 / Ni'
czyli Λ2 = 10,0873
Po odczytaniu z tablicy nr 5 prawdopodobieństwo wynosi:
P = 0,096
Jest ono większe od 0,01 więc rozkład ten możemy uznać za rozkład normalny
Wykres 1 Histogram
Wykres 2 Rozkład idealny
4. Wnioski
Ten mechaniczny model rozkładu jakim jest tablica Galtona pozwala wyraźnie stwierdzić mechanizmy rządzące prawami rozkładu i hierarchią zdarzeń prawdopodobnych. Ten mechaniczny przykład jest jednym z najbardziej obrazowych doświadczeń przez nas wykonywanych. Poza tym jest bodaj jedynym doświadczeniem gdzie dokładność obliczeń nie zależy od dokładności w pomiarach (trudno się pomylić przy liczeniu kulek).
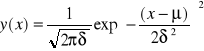
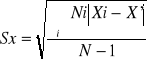
Wyszukiwarka
Podobne podstrony:
GRUPA C, inżynieria ochrony środowiska kalisz, z mix inżynieria środowiska moje z ioś pwsz kalisz
Sprawko metka moje!!, grupa operacyjna
Czym jest grupa, BHP Moje, SZKOLA, Semestr I
Grupa, WNPiD, moje, ChomikBox, prawo gospodarcze unii europejskiej
GRUPA D, inżynieria ochrony środowiska kalisz, z mix inżynieria środowiska moje z ioś pwsz kalisz
test poprawkowy grupa 1
19 183 Samobójstwo Grupa EE1 Pedagogikaid 18250 ppt
Grupa 171, Podstawy zarządzania
Grupa XVI
hatala,januszyk grupa 2a prez 1
pilot a grupa
Podtopienie moje
Wykład 6 Rodzina jako grupa społeczna
Projekt grupa 3 2
Grupa rówieśnicza jako środowisko wychowawcze ptt(1)
Podklad przyklad M4
Praktyczna Nauka Języka Rosyjskiego Moje notatki (leksyka)2
Grupa przestrzenna id 196528 Nieznany
więcej podobnych podstron