Liczby rzeczywiste jest to zbiór liczb wymiernych i niewymiernych. Liczba wymierna to taka liczba, którą można zapisać w postaci ułamka zwykłego, gdzie licznik i mianownik będą liczbami całkowitymi przy czym mianownik będzie różny od zera. Liczby niewymierne są to liczby rzeczywiste, których nie można przedstawić w formie ułamka zwykłego n/m. Liczby całkowite to zbiór liczb wymiernych, naturalnych (1, 2, 3, 4, ...), zera oraz liczb przeciwnych do naturalnych (-1, -2, -3, ...). Liczby naturalne to zbiór liczb całkowitych dodatnich oraz zero. Liczba pierwsza - liczba naturalna, która ma dokładnie dwa dzielniki naturalne: jedynkę i siebie samą, np. 2,3,5,7,11,13,17,19,23 Działania na potęgach :  a^m∙a^n=a^m+n a^m/ a^n= a^m-n (a^m)^n= a^m∙n (a∙b)^n =a^n∙b^n (a/b)^n= a^n/b^n Działania na pierwiastkach :     Wzory skróconego mnożenia :  (a+b)^2=a^2+2ab+b^2 (a-b)^2=a^2-2ab+b^2 (a^2-b^2)=(a-b)-(a+b) (a+b)^3=a^3+3a^2b+3ab^2+b^3 (a-b)^3=a^3-3a^2b+3ab^2-b^3 a^3+b^3= (a+b)(a^2-ab+b^2) a^3-b^3= (a-b)(a^2+ab+b^2) 1	Funkcja Liniowa f(x)= ax+b : własności Miejsce zerowe funkcji jest punktem, w którym funkcja przecina oś OX, oblicza się je z x0= -b/a   Monotoniczność funkcji liniowej a>0 funkcja rosnąca a<0 funkcja malejąca a=0 funkcja stała Parzystość Funkcja jest parzysta, gdy a=0 (funkcja stała). Funkcja jest nieparzysta, gdy b=0 (przechodzi przez środek układu wsp.). Różnowartościowość Funkcja jest różnowartościowa, jeśli a≠0, w przeciwnym wypadku nie jest różnowartościowa (jest stała i zawsze przyjmuje tę samą wartość). Okresowość a≠0funkcja nie jest okresowa. a=0funkcja jest okresowa (stała), jej okresem jest każda liczba R. Wykresy dwóch funkcji Jeśli porównać wykresy dwóch funkcji, to mogą one być: równoległe, gdy a1 = a2 - oba współczynniki są równe prostopadłe, gdy a1= -1/ a2 Warunki równoległości i prostopadłości prostych. Dane są dwie proste: k : y =ax + b l : y = ax +b. Warunek równoległości prostych. Proste w układzie współrzędnych są równoległe wtedy i tylko wtedy, gdy współczynniki kierunkowe tych prostych są równe: k || l a=c wzór funkcji równoległej: y= - ⅓x +b Warunek prostopadłości prostych. Proste w układzie współrzędnych są prostopadłe wtedy i tylko wtedy, gdy iloczyn ich współczynników kierunkowych jest równy -1: k┴l a∙c = -1 wzór f. prostopadłej : y= - 2/3 x+b x- odcięta y rzędna 2
	Aby obliczyć współczynnik a należy odjąć współrzędne Y1-X1 i Y2-X2 a następnie podzielić je przez siebie np. Punkty A=(-4;2) oraz B=(2;6) są symetryczne względem prostej k. Wyznacz równanie prostej. a= 6-2 / 2+4 = 2/3 2= 2/3 * (-4) +b b= 4 2/3 więc y= 2/3 x + 4 2/3 Następnie obliczamy środek symetrii poprzez wyliczenie średniej z y i x -4 +2 = -2 -2/2 = -1 6+2=8 8/2= 4 Jego współrzędne to O=(-1,4) Następnie aby obliczyć współczynnik drugiego równania korzystamy ze wzoru a= -1/a1 a1- to to pierwsze a mając a wyliczasz b równanie symetralnej do tego zadania: y= - 1 ½ x+ 2 ½ Wzór ogólny: y=ax^2+bx+c Jeśli a>0 to: Zw=<0;+∞) f maleje (-∞;0> i rośnie <0;+ ∞) Funkcja nie przyjmuje wartości największej i dla argumentu 0 przyjmuje wartość najmniejszą- 0 Ramiona zwrócone są do góry. Jeśli a<0 właściwości są odwrotne. Wzór postaci kanonicznej: y= a(x-p)^2 +q Jeśli chcemy przesunąć wykres o wektor v= [p,q] to xw= współrzędna x + p= p i yw= wsp. y +q= q Wierzchołek= [p,q] lub x1+x2 /2 p= - b/2a q= - ∆/4a ∆= b^2-4ac Aby znaleźć postać iloczynową ∆ > 0 czyli być na plusie. Wtedy wyliczamy 2 miejsca „0”: x1= ^-b-√^∆/2a x2= ^-b+√^∆/2a Wzór funkcji w post. Iloczynowej to: f(x)=a(x-x1)(x-x2) Gdy ∆ wynosi 0 ma 1 miejsce zerowe które obliczamy ze wzoru: x0=-b/2a Wtedy postać wygląda tak: f(x)= a(x-­x0)^2 Gdy ∆ jest mniejsze od 0 postać iloczynowa nie istnieje 3	Wzór funkcji kwadratowej y=ax^2+bx+c można przekształcić do postaci kanonicznej y= a(x-p)^2 +q za pomocą wzorów na p i q (powyżej) a∙q >0 ∆ <0 miejsce zerowe nie istnieje a∙q= 0 ∆ =0 jest jedno miejsce zerowe a∙q< 0 ∆ >0 są 2 miejsca zerowe w tym wypadku -2∙8 < 0 czyli ∆ >0 mamy więc 2 miejsca 0 Aby naszkicować wykres funkcji kwadratowej: - Podajemy współrzędne punktu przecięcia wykresu z OY- (0,c) - Wyznaczamy p i q czyli wsp. wierzchołka - obliczamy msc „0” - Zaznaczamy msc „0” i sprawdzamy czy odległość między nimi podzielona na 2 wynosi tyle co współczynnik a - Rysujemy parabolę Aby obliczyć pkt przecięcia z OY podstawiamy za x 0 Rozwiązywanie równań kwadratowych to nic innego tylko znalezienie msc „0” więc wszystko przyrównujemy do 0. Następnie szukamy ∆ zgodnie z powyższymi warunkami równanie może mieć 1 lub 2 rozwiązania. Właśnie x1 i x2 są rozwiązaniami. loga1=0 np. log31=0 logab=c a^cb logaa^k=k logax^k=k logax a^loga x=x loga(b∙c)= logab+ logac logab/c= logab - logac logab= logcb / logca 4
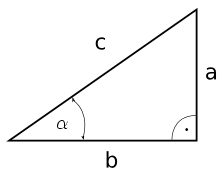
	Sinusem kąta ostrego α nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta α do przeciwprostokątnej Sin α= a/c Cosinusem kąta ostrego α nazywamy stosunek przyprostokątnej leżącej przy kącie α do przeciwprostokątnej Cos α=b/c Tangensem kąta ostrego α nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta α do przyprostokątnej leżącej przy kącie α Tg α= a/c Cotangensem kąta ostrego α nazywamy stosunek przyprostokątnej leżącej przy kącie α do przyprostokątnej leżącej naprzeciw kąta α Ctg α= b/a 30^o 45^o 60^o Sin α ½ √2/2 √3/2 Cos α √3/2 √2/2 ½ Tg α √3/3 1 √3 Ctg α √3 1 √3/3 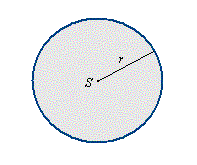Pole koła P = πr^2 Długość okręgu L = 2πr Długość łuku l=α/360°·2πr Pole wycinka koła o kącie środkowym α P=α/360° ·πr^2 Pole odcinka koła o kącie środkowym α P=α/360° πr^2 - r^2sinα /2 5	P prostokąta= a∙b Pole kwadratu= a∙a Przekątna kwadratu a√2 P równoległ. P= a∙h= a∙b∙sinα P rombu= P=a∙h= d1∙d2 / 2= a^2 sinα d1 i d2 są przekątnymi P trapezu: P= (a+b)∙h /2 Jeżeli czworokąt wypukły można wpisać w koło to P= r∙p p= ½ obwodu r- promień Jeżeli przekątne czworokąta mają dł d1 i d2 i przecinają się pod kątem ostrym α to P= ½∙d1∙d2∙ sinα Jeżeli przekątne czworokąta mają dł d1∙d2 i przecinają się pod kątem ostrym to P= ½∙d1∙d2 Stosunek pól figur podobnych równa się kwadratowi skali. (najpierw obliczamy pola, a potem dzielimy je przez siebie- wychodzi skala do kwadratu) Obw = a + b + c + d P=1/2 (a+b)·h e = a+b /2 a= 2x+b x= a-b /2 a=a+b /2 y= a+b / 2 (tylko w równoramiennym, a y to a= 2x+y) Ob = 4a P = a · h = a2 · sinα P=1/2 d1·d2 d= a√2 - przekątna a+c=b+d liczba przekątnych w nkącie wynosi n(n-3) /2 suma kątów kąta wynosi 180^o(n-2) w dowolnym kącie wypukłym suma kątów zewnętrznych wynosi 720^o 6
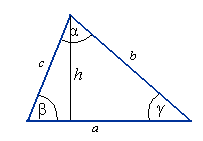
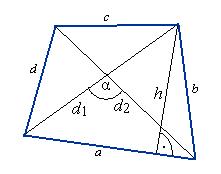
	Obw = a + b + c P=½ah P= ½ ab sinγ =½ bc sinα = ½ ac sinβ P= /p(p-a) (p-b)(p-c) / (// pod pierwiastkiem) gdzie p=½ (a+b+c) - wzór Herona) R=abc/4P - (promień okręgu opisanego), r= P/p- (promień okręgu wpisanego). Obw= a + b + c + d P=½d1·d2·sinα d1, d2 - przekątne czworokąta, α - kąt zawarty między przekątnymi h - wysokość czworokąta Pole czworokąta wpisanego w okrąg: P= /(p-a) (p-b) (p-c) (p-d)/ gdzie p= ½ (a+b+c+d) Ob = 2a + 2b P = a · h = a · b · sinα P=1/2d1·d2·sinγ Ob = 2a + 2b P = a · b d= /a2+b2/ Ob = 4a P = a2 P=1/2d2 d=a√2 7	Wektory: v=(A;B) dla A=(xA;yA) i B= (xB;yB) v= (xB-xA ; yB-yA) Wektory są przeciwne gdy A+B=0 Środek wektora/odcinka: S= ( xA+xB /2 ; yA+yB /2) Proste: równanie kierunkowe prostej k:y=ax+b a- współczynnik a= tg α tg(180^o- α)=-tg α postać ogólna: k: Ax+By+C=0 => A^2+B^2≠0 Równoległość/prostopadłość: l: y=ax+b k:y=cx+d l || k a=c lub A1x+B1y+C1=0 k:A2x+B2y+C2=0 l || k A1/ A2 = B1/ B2 l┴k a∙c=-1 lub l┴k A1A2+ B1B2=0 Odległość punktu od prostej: d=|Ax0+By0+C| / [A^2+B^2] => [] pod pierwiastkiem równanie okręgu: (x-a)^2+(y-b)^2=r^2 x^2+y^2-2ax-2by+C=0 gdzie c=a^2+b^2-r^2 SP=[x-xs ; y-ys] Wyznaczanie dziedziny funkcji: wiec jeśli masz jakiś ułamek -> wtedy to co w mianowniku musi być różne od zera ! jeżeli masz jakiś pierwiastek -> wówczas pod pierwiastkiem liczba nie może być ujemna, może być zerem i dodatnia dlatego pisze sie większa lub równa zero 8

S=(x_s;y_s) lub (a;b)

P(x;y)

---