W trapezie ABCD trzy boki mają długość AD=6 cm DC=8 cm BC= 9 cm. Ponadto |ADC|=|ACB| Wykaż, że trójkąty ACD i BCA są podobne Oblicz dł boku AB. DA/DC = CB/CA 6/8 = 9/CA CA=12 AB=? DA/CA=CB/AB 6/12=9/AB AB=18	W czworokąt ABCD można wpisać okrąg oraz miara AB równa się 5 cm i miara CD równa się 13 cm. Obrazem czworokąta ABCD o podobieństwie o skali ¼ jest czworokąt A1B1C1D1. Oblicz obwód czworokąta A1B1C1D1. AB + CD = BC+AD = 5+13 = 18 ObwABCD= 36 cm k= ¼ ObwA1B1C1D1=? ObwA1B1C1D1 /ObwABCD = ¼ ObwA1B1C1D1 / 36=1/4 mnoż. na krzyż 4∙ ObwA1B1C1D1=36 ObwA1B1C1D1= 9 cm	W prostokącie ABCD długości boków pozostają w stosunku 3:4. obrazem prostokąta ABCD w podobieństwie o skali 2/3 jest prostokąt którego przekątna ma długość 7,5 cm. oblicz różnice obwodów tych prostokątów. (3x)²+(4x)²=7,5² 9x²+16x²=56,25 25x²=56,25 x²=2,25 2,25∙9=20,25 z tego pierwiastek to=4,5 2,25∙16=36 pierwiastek=6 2∙4,5+2∙6=21 21∙3/2=31,5 31,5-21=10,5
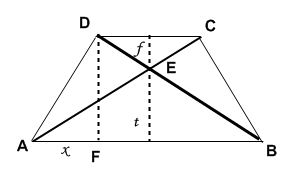
Krótsza przekątna rombu ma dł 12cm, a bok jest o 2 cm dłuższy od połowy drugiej przekątnej. Oblicz dł. boku rombu. d2=12 cm d1=2x a= 2 cm+x x²+36=(x+2)² x²+36=x²+4x+4 4x=32 x=8	W trapezie równoramiennym podstawy mają długość 25 cm i 7 cm, a przekątna ma długość 20 cm. Oblicz odległości punktu przecięcia przekątnych od obu podstaw. 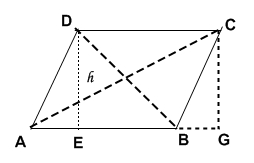t+f=h |DB|=20 |FB|= a+b /2 |FB|= 7+25 /2 = 16 h^2+|FB^|2=|DB|^2 h^2 =20^2-16^2 h^2= 144+256 h=12 t+f=12 ∆ABE~∆ECD AB/DC =t/f 25/7=t/f | ∙ f 25/7f + f =12 32/7 f =12 / : 32/7 f= 12/ 32/7 = 12/1 ∙ 7/32 f= 21/8 = 2 5/8 t= 12- 2 5/8 = 9 3/8	W równoległoboku ABCD wysokość DE ma 8cm i dzieli bok AB na odcinki długości AE=4,5 cm i EB=6cm. Oblicz długość przekątnych tego równoległoboku. |BD|^2=|EB|^2+|ED|^2 |BD|^2= 6^2+8^2 |BD|^2= 36+64 |BD|^2=100 |BD|= 10 BG=AE BG+AE + EB = 15 cm |AC|^2= 15^2+8^2 |AC|^2= 225+64 =289 AC = 17
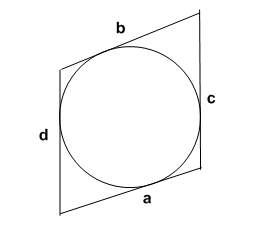
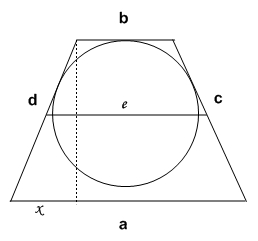
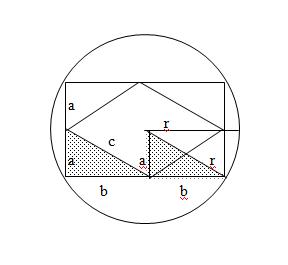
W trapez równoramienny wpisano okrąg o promieniu r= 4 cm. Ramię trapezu ma długość 10 cm. Punkty styczności okręgu z ramionami trapezu dzielą obwód trapezu na dwie części. Oblicz stosunek tych części. 4y/4x=y/x x+y=10 a+b=2c a+b=2a t (ten kawałeczek)= a-b/2 t^2+h^2=c^2 t^2=100-64 t^2=36 t=6 6= a-b/2 |∙2 a-b=12 2x-2y=12 Układ równań: x-y=6 x+y=10 2x=16 x=8 y=2 y/x=2/8=1/4	W okrąg, którego promień ma długość 10cm, wpisano prostokąt. Środki kolejnych boków prostokąta połączono odcinkami. Oblicz obwód otrzymanego czworokąta. W szarych trójkątach można zastosować tw Pitagorasa. a²+b²=c² a²+b²=r² Wynika stąd, że c²=r² c = r c = 10 Obwód L = 4c L = 4*10 L = 40	Obwód trapezu równoramiennego jest równy 30 cm, a odcinek łączący środki przekątnych trapezu ma długość 1,5 cm. Wiedząc, że w ten trapez można wpisać okrąg, oblicz długości podstaw trapezu a+b=2c a=? b=? h=2r=? a+b+2c= 30 2c+2c=30 c=7,5 a+b=15 f= a-b /2 1,5= a-b /2 ukł równ. w następnej linijce a-b=3 a+b= 15 a=9 b=6
e = a+b /2 a= 2x+b x= a-b /2 a=a+b /2 y= a+b / 2 (tylko w równoramiennym, a y to a= 2x+y) d= a√2 - przekątna a+c=b+d liczba przekątnych w nkącie wynosi n(n-3) /2 suma kątów kąta wynosi 180^o(n-2) w dowolnym kącie wypukłym suma kątó zewnętrznych wynosi 720^o	W trapez ABCD wpisano okrąg. Ramię BC trapezu zostało podzielone przez punkt styczności S na odcinki długości |CS|= 1oraz |BS|=9cm. Obliczymy długość promienia okręgu w następujący sposób. Niech E i F będą punktami styczności okręgu z podstawami trapezu, G będzie spodkiem wysokości trapezu poprowadzonej z wierzchołka C. r niech oznacza długość promienia okręgu wpisanego w ten trapez. 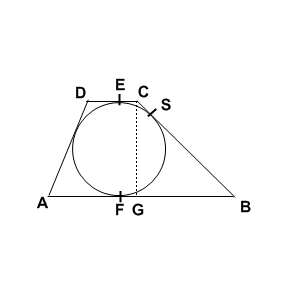|FB|=|BS| |EC|=|CS| |FB|= 9cm |EC|= 1cm. |FG|=|EC|=1cm |GB|=|FB|-|FG|=8cm |CG|^2+|GB|^2=|BC|^2 |CG|^2+8^2=10^2 |CG|^2=100-64 |CG|= 6 |CG|= 2r 6=2r r=3

---