9 1 0.45 0.05 1.548254401E-0001 3.2E-0004

9 2 0.45 0.10 3.058385559E-0001 6.3E-0004

9 3 0.45 0.15 4.493209010E-0001 9.2E-0004

9 4 0.45 0.20 5.817394691E-0001 1.1E-0003

9 5 0.45 0.25 6.998336785E-0001 1.4E-0003

9 6 0.45 0.30 8.006956589E-0001 1.6E-0003

9 7 0.45 0.35 8.818418543E-0001 1.8E-0003

9 8 0.45 0.40 9.412741765E-0001 1.9E-0003

9 9 0.45 0.45 9.775292047E-0001 2.0E-0003

9 10 0.45 0.50 9.897142202E-0001 2.0E-0003

. . . . . . . . . . . . . . . . . . . . . . . . . . . .

Przedstawione porównanie omawianych w tym rozdziale i w rozdziale poprzednim metod iteracyjnych rozwiązywania układów równań liniowych, pojawiających się w metodach różnicowych dla równań eliptycznych, dokonane dla dwóch szczególnych zagadnień na rzadkich siatkach nie pozwalają na pełne zorientowanie się w efektywności i skuteczności poszczególnych metod. Liczba iteracji niezbędnych do uzyskania rozwiązania zależy od liczby oczek siatki i np. dla zagadnienia (7.135) po przyjęciu: liczby iteracji były następujące:

- metoda Gaussa-Seidela: 976,

- metoda Stone'a: 250,

- optymalna metoda relaksacji: 83,

- metoda sprzężonych gradientów: 37.

Należy przy tym wziąć pod uwagę bardzo istotny fakt, że sama liczba iteracji nie jest wystarczającym wskaźnikiem do porównywania i oceny poszczególnych metod iteracyjnych, gdyż liczba operacji arytmetycznych niezbędnych do otrzymania następnego przybliżenia w każdej metodzie jest inna.

Ćwiczenia

7.1. Metoda jawna pierwszego rzędu, metoda niejawna pierwszego rzędu oraz metoda Cranka-Nicolsona dla jednowymiarowego równania dyfuzji (7.15) są szczególnymi przypadkami ogólnego algorytmu określonego wzorem

gdzie
Metoda jawna pierwszego rzędu odpowiada parametrowi metoda niejawna pierwszego rzędu - parametrowi metoda Cranka-Nicolsona - parametrowi:
Należy zbadać stabilność tego schematu różnicowego oraz udowodnić, że w szczególnym przypadku dla

błąd aproksymacji jest

7.2. Zbadać stabilność schematu różnicowego

dla równania (7.15) z dodatkowym parametrem
W przypadku sche-mat ten jest równoważny metodzie niejawnej pierwszego rzędu. Ponadto należy udo-wodnić, że dla
błąd aproksymacji równania (7.15) wynosi

7.3. Wykorzystać zmodyfikowany program 7.1 do rozwiązywania równania (7.15) z warunkiem początkowym (7.32) i warunkami brzegowymi:

Uzyskane wyniki porównać z rozwiązaniem dokładnym

gdzie

7.4. Zbadać stabilność schematu różnicowego

aproksymującego równanie falowe drugiego rzędu

7.5. Uogólnić metody: „upwind”, skokową i Laxa-Wendroffa dla dwuwymiarowego równania adwekcji (7.86) i wyprowadzić dla tych metod warunki nakładane na krok czasowy

7.6. Zmienić działanie programu 7.2 w taki sposób, aby możliwe było rozwiązywanie jednowymiarowego równania adwekcji dla dowolnej prędkości

i dla dowolnego warunku początkowego

7.7. Uogólnić schemat różnicowy (7.96) dla prostokątnej siatki utworzonej przez proste:

i następnie dla tej siatki wyprowadzić wzory dla metod iteracyjnych: Jacobiego, Gaussa-Seidela i relaksacji, których szczególnymi przypadkami będą wzory (7.104) -(7.106).

7.8. Za pomocą zmodyfikowanych programów 7.3 ÷ 7.5 rozwiązać równanie Poissona

z warunkami brzegowymi:

Otrzymane rozwiązanie porównać z rozwiązaniem dokładnym

7.9. Wprowadzić w programie 7.3 drugą alternatywę obliczeń, umożliwiającą wyznaczenie rozwiązania zagadnienia (7.108) za pomocą metod iteracyjnych: Jacobiego, Gaussa-Seidela i relaksacji - otrzymanych przy wykorzystaniu schematów (7.99) do aproksymacji operatora Laplace'a

7.10. Opracować program komputerowy przeznaczony do rozwiązywania zagadnienia brzegowego (7.108) - (7.109) metodą różnic skończonych (7.100). Do rozwiązywania równania macierzowego (7.101) należy zastosować algorytm metody eliminacji Gaussa (2.101) ÷ (2.103) z uwzględnieniem szczególnej postaci macierzy leżących na przekątnej głównej i przekątnych pobocznych.

7.11. Przy wykorzystaniu programów 7.3 ÷ 7.5 przetestować rozważane w rozdziałach 7.5 i 7.6 metody iteracyjne rozwiązywania siatkowych równań eliptycznych dla zagadnienia:

którego rozwiązaniem dokładnym jest funkcja

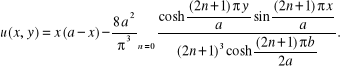
520 7. Równania różniczkowe cząstkowe

Ćwiczenia 517

---