WYKŁAD 13

EKSTREMA WARUNKOWE

Mówimy, że funkcja wielu zmiennych
osiąga w punkcie
minimum lokalne warunkowe (maksimum lokalne warunkowe) przy warunku
, jeżeli istnieje otoczenie U punktu
, takie że dla każdego punktu
i spełniającego warunek
spełniona jest nierówność

Aby znaleźć takie ekstremum, budujemy funkcję (n+1)-zmiennych
postaci

Funkcja L nazywa się funkcją Lagrange'a, a metodę szukania ekstremów warunkowych z użyciem tej funkcji - metodą mnożników Lagrange'a. Liczbę
nazywamy mnożnikiem Lagrange'a.

Tw. (warunek konieczny istnienia ekstremum warunkowego) Załóżmy, że funkcja
jest określona w pewnym otoczeniu punktu
, i wraz z funkcją
posiada w tym punkcie wszystkie pochodne cząstkowe pierwszego rzędu. Jeżeli funkcja f osiąga w punkcie
ekstremum lokalne przy warunku
, to wszystkie pochodne cząstkowe funkcji Lagrange'a L w tym punkcie są równe 0, tzn.

Punkt
, dla którego są spełnione ostatnie równości nazywa się punktem stacjonarnym funkcji L Do warunku dostatecznego potrzebna jest macierz, zwana hesjanem funkcji Lagrange'a

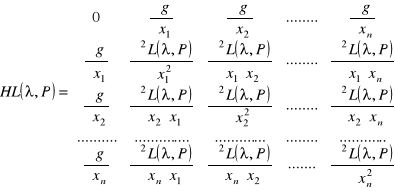
Oznaczmy

,

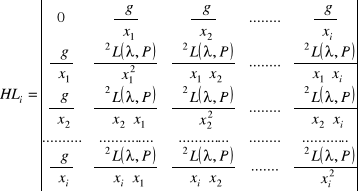
Uwaga.
jest wyznacznikiem o wymiarach
i jest funkcją
zmiennych

Tw. (warunek dostateczny istnienia ekstremum warunkowego) Niech punkt
będzie punktem stacjonarnym funkcji Lagrange'a, mającej ciągłe pochodne cząstkowe drugiego rzędu w pewnym otoczeniu tego punktu.

Jeżeli dla i=2,3,…,n spełnione są nierówności
, to w punkcie
funkcja f osiąga minimum warunkowe przy warunku
.

Jeżeli dla i=2,3…,n spełnione są nierówności
, to w punkcie
funkcja f osiąga maksimum warunkowe przy warunku
.

W szczególnym przypadku otrzymujemy:

Tw. (warunek dostateczny istnienia ekstremum warunkowego dla n=2) Załóżmy, że funkcje
oraz
mają w otoczeniu punktu
ciągłe pochodne cząstkowe rzędu drugiego. Niech
będzie punktem stacjonarnym funkcji Lagrange'a

1. Jeżeli
, to funkcja f osiąga w punkcie
minimum lokalne przy warunku

2. . Jeżeli
, to funkcja f osiąga w punkcie
maksimum lokalne przy warunku

Tw. (warunek dostateczny istnienia ekstremum warunkowego dla n=3) Załóżmy, że funkcje
oraz
mają w otoczeniu punktu
ciągłe pochodne cząstkowe rzędu drugiego. Niech
będzie punktem stacjonarnym funkcji Lagrange'a

1. Jeżeli
, to funkcja f osiąga w punkcie
minimum lokalne przy warunku

2. Jeżeli
, to funkcja f osiąga w punkcie
maksimum lokalne przy warunku
.

Można udowodnić, że funkcja ciągła
, określona na domkniętym i ograniczonym podzbiorze A przestrzeni
osiąga wartość najmniejszą i największą. Wartości te nazywają się ekstremami globalnymi funkcji f na zbiorze A. Poszukujemy ich podobnie, jak w przypadku funkcji jednej zmiennej:

1. Szukamy punktów stacjonarnych funkcji f, należących do zbioru A,

2. Szukamy punktów stacjonarnych funkcji Lagrange'a
   , gdzie
   opisuje brzeg zbioru A (lub, jeżeli to możliwe, wyliczając jedną ze zmiennych z warunku i szukając ekstremów funkcji o mniejszej ilości zmiennych)

3. Liczymy wartości funkcji f w znalezionych punktach i w punktach, w których łączą się różne krzywe, opisujące brzeg zbioru A,

4. Ze znalezionych wartości wybieramy najmniejszą i największą