Wartość własna o module max: 6.1622777E+0000

Krotność max wartości własnej - q: 2

Liczba potęgowań macierzy zadanej - m: 7

Macierz odwrotna:

wiersz nr 1

-5.0000E+0000 3.0000E+0000 0.0000E+0000 0.0000E+0000

wiersz nr 2

2.0000E+0000 -1.0000E+0000 0.0000E+0000 0.0000E+0000

wiersz nr 3

0.0000E+0000 0.0000E+0000 -5.0000E+0000 3.0000E+0000

wiersz nr 4

0.0000E+0000 0.0000E+0000 2.0000E+0000 -1.0000E+0000

Wartość własna o module min: -1.6227766E-0001

Krotność min wartości własnej - q: 2

Liczba potęgowań macierzy odwrotnej - m: 6

ĆWICZENIA

2.1. Dana jest macierz
Napisać program transponowania tej macierzy. Wydrukować macierz transponowaną przy założeniu, że na szerokości strony papieru mieści się pięć kolumn liczb.

2.2. Opracować program obliczania norm macierzy (2.31) - (2.33) dla danej macierzy prostokątnej

2.3. Przy wykorzystaniu programów 2.1 ÷ 2.3 rozwiązać układ równań liniowych:

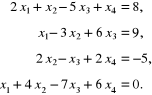
Otrzymane wyniki należy porównać z rozwiązaniem dokładnym:

2.4. Za pomocą programów 2.1 ÷ 2.3 rozwiązać następujące układy równań liniowych:

a)

b)

c)

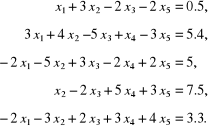
d)

e)

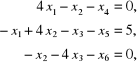
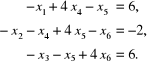
2.5. Wyznaczyć macierze odwrotne do macierzy współczynników układów równań liniowych rozwiązywanych w przykładach 2.3 i 2.4 przy wykorzystaniu programów 2.1 i 2.2.

2.6. Wyprowadzić wzory określające elementy macierzy oraz i następnie wykorzystać te wzory w zmodyfikowanym programie 2.2 do obliczania macierzy

2.7. Napisać program przeznaczony do odwracania macierzy kwadratowej A stopnia n przez podział na bloki przy wykorzystaniu procedury (2.58).

Macierz A możemy przedstawić w postaci

gdzie P i S są macierzami kwadratowymi odpowiednio stopnia p i s, Q jest macierzą o wymiarach
, a R - macierzą o wymiarach
Podobnie napiszemy

gdzie K, L, M i N mają takie same wymiary, jak wymiary odpowiednich macierzy P, Q, R i S. Ponieważ możemy więc napisać dwa układy równań:

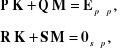
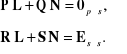
Z pierwszego z tych układów równań wyznaczamy macierze K i M :

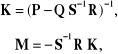
z drugiego - macierze N i L :

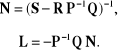
2.8. Zmodyfikować program 2.4 dodając w nim jeszcze jeden wariant obliczeń pozwalający na wyznaczanie maksymalnej co do modułu zespolonej wartości własnej i jednocześnie minimalnej co do modułu wartości własnej będącej pierwiastkiem rzeczywistym jedno- lub q-krotnym równania charakterystycznego.

124 2. Układy równań liniowych

Ćwiczenia 121

---