Zagadnienie 34.

Wprowadzenie niewiadomej i równania w klasie I dla poszerzenia możliwości wykonywania obliczeń oraz dla dalszych sposobów rozwiązywania zadań tekstowych. Metody rozwiązywania równań.

Rozwiązywanie równań na etapie nauczania początkowego nie powinno być celem samym w sobie, lecz służyć rozwiązywaniu trudniejszych zadań tekstowych i kształceniu rozumienia działań.

Równanie w klasach I-III powinno być dla ucznia zagadką, polegającą na poszukiwaniu nieznanej liczby. Jego rozwiązanie ma służyć pogłębianiu rozumienia liczb i działań na liczbach. Na tym etapie nauczania nie chodzi o opanowanie umiejętności rozwiązywania i przekształcania równań.

Rozwiązywanie równań powinno się rozpocząć w klasie I, rozpoczynając od ćwiczeń słownych typu:

• Do pewnej liczby dodałem 5 i otrzymałem 8. Jaka to liczba?

• Myślę o liczbie, która jest o 6 większa od 2. Jaka to liczba?

Potem zapisywanie przy użyciu grafów, drzewek, a na końcu dopiero zapisy przy użyciu symboli działań.

Zapisywanie równań w klasach początkowych

• tradycyjnie z użyciem znaku =

3 + ... = 11

3 + ? = 11

3 + x = 11

Słownie wypowiadamy je w następujący sposób: Jaką liczbę dodam do 3, aby otrzymać 11.

• za pomocą grafu

Czytamy go zgodnie ze zwrotem strzałki.

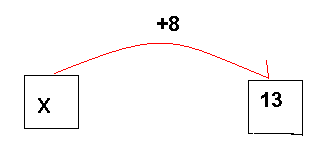
• za pomocą drzewka

Rozwiązywanie równań

1. rozwiązywanie przez symulację - w tej metodzie wykorzystujemy:

• konkretne przedmioty - jest to tzw. symulacja manipulacyjna

• schematy graficzne - wówczas mamy do czynienia z symulacją graficznaą

PRZYKŁAD:

Miałem pięć modeli samochodów. Na imieniny dostałem jeszcze kilka. Teraz mam 13 modeli. Ile modeli dostałem na imieniny?

• symulacja manipulacyjna

Uczeń symuluje przedstawioną sytuację na patyczkach. Po prawej stronie układa 13 patyczków. Następnie po lewej kładzie 5 i dosuwa tyle, aby po prawej i po lewej miał po tyle samo. Zauważa, że musiał dosunąć 8.

׀׀׀׀׀ + ׀׀׀׀׀׀׀׀ = ׀׀׀׀׀׀׀׀׀׀׀׀׀

5 x 13

• symulacja graficzna

Po prawej stronie uczeń rysuje 13 kół. Po lewej również 13 (ponieważ lewa strona musi być równa prawej) ale 5 kół zamalowuje, bo tyle ich było na początku. Nie zamalowane koła po lewej stronie to poszukiwana liczba.

●●●●● ○○○○○○○○ = ○○○○○○○○○○○○○

W każdym przypadku dla danego równania uczeń buduje model symulacyjny, rozwiązuje go
i rozwiązanie to przenosi na właściwe zadanie.

2. rozwiązywanie za pomocą grafu

x + 8 = 13

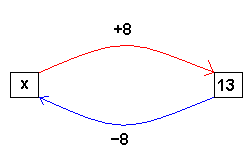
x = 13 - 8

c) rozwiązywanie za pomocą tabelki funkcyjnej

Konstruujemy tabelę podwójną. W pierwszym rzędzie piszemy kolejne liczby: 0, 1, 2, 3, ……… Przy strzałce z boku piszemy drugi składnik.

Analizując tabelę uczeń dochodzi do wniosku, że sumę 13 uzyskuje dodając 8 do

liczby 5, a więc x = 5

d) Rozwiązywanie w oparciu o prawa działań

Równania możemy tez rozwiązywać, korzystając ze związków między działaniami: dodawaniem
i odejmowaniem oraz mnożeniem i dzieleniem. Równanie x + 8 = 13 rozwiążemy wykorzystując związki między dodawaniem i odejmowaniem. Uczeń rozumuje tak: jeśli do pewnej liczby dodam 8 i otrzymam 13, to odejmując od 13 liczbę 8 otrzymam szukaną liczbę, ponieważ odejmowanie jest odwrotne do dodawania i aby obliczyć niewiadomy składnik należy od sumy odjąć składnik, który znamy.

Zapisujemy: x + 8 = 13

więc: 13 - 8 = x

5 = x

x = 5

Inne metody rozwiązywania równań poznają uczniowie w dalszym etapie kształcenia.

1

---