Wydział : FiTJ	Imię i nazwisko : Rafał Szuman, Rafał Sikora				rok II	Grupa 3			Zespół 10
Pracownia fizyczna I	Temat ćwiczenia : Drgania elektromagnetyczne obwodu RLC							Ćwiczenie nr: 61
Data wykonania:		Data oddania:	Zwrot do poprawy:	Data oddania:			Data zaliczenia:			Ocena:

Cel ćwiczenia

Obserwacja drgań tłumionych i przebiegów aperiodycznych w obwodzie LCR. Pomiar i interpretacja parametrów opisujących obserwowane przebiegi napięcia U(t). Badanie obwodu LCR jako modelowej realizacji fizycznej liniowego równania różniczkowego dru­giego stopnia.

Wprowadzenie

Zjawisko drgań elektromagnetycznych w obwodzie złożonym z idealnej indukcyjności L i pojemności C jest szczegółowo opisane w podręcznikach. Częstość ω takich niegasnących drgań dana jest wzorem

Rzeczywisty obwód posiada niezerową rezystancję R, na który składa się rezystancja cewki i dodatkowej opornicy.

Zachowanie obwodu, nazywanego obwodem LCR, opisuje równanie różniczkowe

Nie ma łatwego sposobu pomiaru zmiennego w czasie ładunku q(t), ale możemy mierzyć, proporcjonalne do q(t), napięcie kondensatora U(t) = q(t)/C. Równanie powyższe przepisać można dla funkcji U(t) w postaci:

.

Równanie to, w zależności od wartości parametru

,

nazwanego rezystancją krytyczną, ma trzy jakościowo różne rozwiązania.

1. Dla wartości R<R_c otrzymujemy rozwiązanie w postaci funkcji

które reprezentuje gasnące drgania kosinusoidalne. β jest współczynnikiem tłumienia, którego odwrotność odpowiada czasowi po którym amplituda sygnału spadnie o czynnik 1/e. Wartości β i ω wyrażają się przez:

,
,

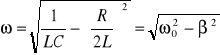
A jest amplitudą niegasnących drgań, a δ jest fazą.

2. Dla wartości R=R_c rozwiązaniem jest funkcja

,

która najszybciej maleje do zera (najszybsze wytłumienie drgania).

3. Dla R>R_c funkcja ma rozwiązanie w postaci

,

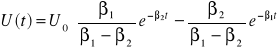
gdzie
,
. Gdy spełnione jest R>>R_c, to powyższą funkcję można przybliżyć funkcją

,

gdzie τ=RC. Na poniższym rysunku zebrane są wszystkie omówione przypadki.

---