PROGRAM 2.1.

Rozwiązywanie układu równań liniowych.

Metoda eliminacji Gaussa z częściowym wyborem

elementu podstawowego.

Liczba równań układu - n = 3

Liczba prawych stron - m = 1

Macierz współczynników:

wiersz nr 1

1.0000000E+0000 -1.0000000E+0000 2.0000000E+0000

wiersz nr 2

2.0000000E+0000 1.0000000E+0000 -1.0000000E+0000

wiersz nr 3

1.0000000E+0000 3.0000000E+0000 -1.0000000E+0000

Wektory prawych stron:

wiersz nr 1

5.0000000E+0000

wiersz nr 2

1.0000000E+0000

wiersz nr 3

4.0000000E+0000

Wyznacznik - det = 1.1000000E+0001

Rozwiązania układów równań:

wiersz nr 1

1.0000000E+0000

wiersz nr 2

2.0000000E+0000

wiersz nr 3

3.0000000E+0000

Macierz odwrotna:

wiersz nr 1

1.8181818E-0001 4.5454545E-0001 -9.0909091E-0002

wiersz nr 2

9.0909091E-0002 -2.7272727E-0001 4.5454545E-0001

wiersz nr 3

4.5454545E-0001 -3.6363636E-0001 2.7272727E-0001

2.4. Metoda Banachiewicza

W metodzie Banachiewicza rozwiązywania układów równań liniowych wykorzystywany jest rozkład macierzy współczynników A

(2.60)

na iloczyn macierzy trójkątnej dolnej L oraz macierzy trójkątnej górnej U - mającej tę własność, że wszystkie elementy jej przekątnej głównej są jedynkami:

(2.61)

Z układu równań (2.60) uzyskujemy
zależności:

.......................................

z których łatwo obliczamy elementy macierzy L :

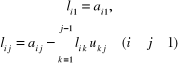
(2.62)

oraz elementy macierzy U :

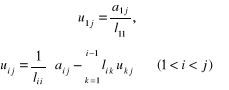
(2.63)

dla j = 2, ..., n, wyznaczając ich elementy naprzemiennie w kolejnych kolumnach.

Podstawiając iloczyn (2.60) do układu równań (2.36) otrzymujemy

(2.64)

stąd następnie po zastąpieniu iloczynu macierzy U przez wektor X wektorem kolumnowym Y

(2.65)

wynika układ równań

(2.66)

W ten sposób wyjściowe zadanie (2.64) zostało zastąpione dwoma prostymi zadaniami (2.65) i (2.66).

Zapisując układ równań (2.66) w postaci macierzowej

po wykonaniu wszystkich mnożeń uzyskamy zależności:

z których można wyznaczyć rekurencyjnie kolejne elementy wektora Y :

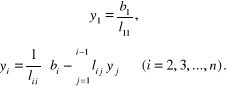
(2.67)

Rozwiązanie natomiast układu równań (2.65), który zapiszemy w postaci rozwiniętej:

odbywa się tak samo jak postępowanie odwrotne w metodzie eliminacji Gaussa (2.54). Mamy więc:

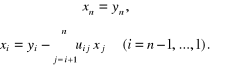
(2.68)

Szczególna odmiana metody Banachiewicza, nazywana też metodą pierwiastków kwadratowych, wykorzystywana jest często do rozwiązywania układów rów-nań liniowych, których macierze współczynników są symetryczne i dodatnio określone. Opiera się ona na twierdzeniu [6], zgodnie z którym dla każdej symetrycznej i dodatnio określonej macierzy A istnieje dokładnie jedna macierz trójkątna dolna L o dodatnich elementach diagonalnych - taka, że

(2.69)

Po dokładnym rozpisaniu równania (2.69)

otrzymujemy zależności:

...............................

które można zapisać za pomocą następujących wzorów ogólnych dla j = 1, 2, ...,

(2.70)

Stąd kolejno obliczamy:

(2.71)

W metodzie pierwiastków kwadratowych otrzymujemy układ dwóch następujących równań:

LY = B, (2.72)

równoważnych układowi wyjściowemu (2.36) z macierzą (2.69) ze współczynnikami (2.71) - (2.72). Rozwiązanie pierwszego z tych układów jest określone wzorami (2.67). W przypadku drugiego z tych układów równań

rozwiązanie jest określone wzorami analogicznymi do wzorów (2.68):

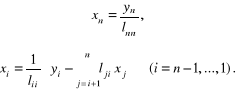
(2.73)

Znając rozkład macierzy A na macierze trójkątne (2.60) - (2.63) lub (2.69) - (2.71) łatwo można obliczyć wyznacznik det A lub wyznaczyć macierz odwrotną . Przypomnijmy, że jeśli to det A = det B ⋅ det C oraz Wyznacznik macierzy trójkątnej jest równy iloczynowi ich elementów diagonalnych, a macierz odwrotna do macierzy trójkątnej jest również macierzą trójkątną.

*

Rozwiązywanie układu równań metodą Banachiewicza jest wykonywane automatycznie w programie 2.2, zorganizowanym w następujący sposób:

1) wczytywanie danych zapisanych w pliku Pr_2_2.dan , zawierających:

- liczby n i m równań i prawych stron w układzie równań liniowych,

- elementy tablicy A[1..n,1..n] i B[1..n,1..m],

2) rozkładanie macierzy współczynników na macierze (2.61) odbywające się w procedurze

Rozklad_LU(n,A,L,U), (2.74)

w której elementy macierzy L i U są zapamiętywane w dwóch tablicach dwuwymiarowych L,U[1..n,1..n],

2) rozwiązywanie układów równań liniowych (2.66) oraz (2.65) przy wykorzystaniu procedury

MetBanach(n,m,L,U,B,det), (2.75)

w której wektory rozwiązań zapisywane są sukcesywnie w tablicy prawych stron B[1..n,1..m], a pod det podstawiana jest wartość wyznacznika det A ,

3) obliczanie macierzy odwrotnej z układów równań (2.55) - (2.56),

4) drukowanie wczytywanych danych i uzyskanych wyników obliczeń.

{Program 2.2}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

const nmax = 20;

type

Tabl = array[1..nmax,1..nmax] of Real;

. . . . . . . . . . . . . . . . . . . .

var

Form3: TForm3;

i,j,k,n,m: Integer;

nazwa: String;

A,B,L,U: Tabl;

plik: Text;

det: Real;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

procedure Rozklad_LU(n: Integer; A: Tabl; var L,U: Tabl);

var

i,j,k: Integer;

sp: Real;

begin

for i:=1 to n do

for j:=1 to n do begin

if j=1 then L[i,j]:=A[i,j]

else L[i,j]:=0;

if j=i then U[i,j]:=1

else U[i,j]:=0;

end;

if Abs(L[1,1])<1e-10 then Halt(1);

for j:=2 to n do

U[1,j]:=A[1,j]/L[1,1];

for i:=2 to n do

L[i,2]:=A[i,2]-L[i,1]*U[1,2];

if Abs(L[2,2])<1e-10 then Halt(1);

for j:=3 to n do begin

for i:=2 to j-1 do begin

sp:=0;

for k:=1 to i-1 do

sp:=sp+L[i,k]*U[k,j];

U[i,j]:=(A[i,j]-sp)/L[i,i];

end;

for i:=j to n do begin

sp:=0;

for k:=1 to j-1 do

sp:=sp+L[i,k]*U[k,j];

L[i,j]:=A[i,j]-sp;

if (i=j) and (Abs(L[i,i])<1e-10) then Halt(1);

end;

end;

end;

procedure MetBanach(n,m: Integer; L,U: Tabl; var B: Tabl;

var det: Real);

var

i,j,k: Integer;

sp: Real;

Y: Tabl;

begin

for k:=1 to m do

Y[1,k]:=B[1,k]/L[1,1];

for i:=2 to n do

for k:=1 to m do begin

sp:=0;

for j:=1 to i-1 do

sp:=sp+L[i,j]*Y[j,k];

Y[i,k]:=(B[i,k]-sp)/L[i,i];

end;

for k:=1 to m do

B[n,k]:=Y[n,k];

for i:=n-1 downto 1 do

for k:=1 to m do begin

sp:=0;

for j:=i+1 to n do

sp:=sp+U[i,j]*B[j,k];

B[i,k]:=Y[i,k]-sp;

end;

det:=1;

for i:=1 to n do

det:=det*L[i,i];

end;

. . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

AssignFile(plik,nazwa);

Reset(plik); Readln(plik,n,m);

for i:=1 to n do begin

for j:=1 to n do

Read(plik,A[i,j]);

for k:=1 to m do

Read(plik,B[i,k]);

end;

CloseFile(plik);

AssignFile(plik,Edit1.Text);

Rewrite(plik); Writeln(plik,'PROGRAM 2.2');

Writeln(plik,'Rozwiązywanie układu równań liniowych.');

Writeln(plik,'Metoda Banachiewicza.'); Writeln(plik);

Writeln(plik,'Liczba równań układu - n =',n:3);

Writeln(plik,'Liczba prawych stron - m =',m:3);

Writeln(plik);

Writeln(plik,'Macierz współczynników:');

for i:=1 to n do begin

Writeln(plik,' wiersz nr ',i:3);

k:=0; Write(plik,' ');

for j:=1 to n do begin

k:=k+1;

if k=5 then begin

k:=0; Writeln(plik);

Write(plik,' ');

end;

Write(plik,' ',A[i,j]:16);

end;

Writeln(plik);

end;

Writeln(plik);

Writeln(plik,'Wektory prawych stron:');

for i:=1 to n do begin

Writeln(plik,' wiersz nr ',i:3);

Write(plik,' ');

for k:=1 to m do

Write(plik,' ',B[i,k]:16);

Writeln(plik);

end;

Writeln(plik);

Rozklad_LU(n,A,L,U);

MetBanach(n,m,L,U,B,det);

Writeln(plik,'Wyznacznik - det = ',det:16);

Writeln(plik);

Writeln(plik,'Rozwiązania układów równań:');

for i:=1 to n do begin

Writeln(plik,' wiersz nr ',i:3);

Write(plik,' ');

for k:=1 to m do

Write(plik,' ',B[i,k]:16);

Writeln(plik);

end;

Writeln(plik);

for i:=1 to n do

for j:=1 to n do

if i=j then B[i,j]:=1

else B[i,j]:=0;

MetBanach(n,n,L,U,B,det);

Writeln(plik,'Macierz odwrotna:');

for i:=1 to n do begin

Writeln(plik,' wiersz nr ',i:3);

k:=0; Write(plik,' ');

for j:=1 to n do begin

k:=k+1;

if k=5 then begin

k:=0; Writeln(plik);

Write(plik,' ');

end;

Write(plik,' ',B[i,j]:16);

end;

Writeln(plik);

end;

Writeln(plik); CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(Edit1.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

if OpenDialog1.Execute then begin

nazwa:=OpenDialog1.FileName;

Dane.Lines.LoadFromFile(nazwa);

end;

end;

procedure TForm3.BitBtn4Click(Sender: TObject);

begin

Close;

end;

76 2. Układy równań liniowych

2.4. Metoda Banachiewicza 77

---