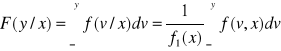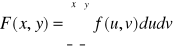
WYKŁAD 6
(by katja``)
Dwuwymiarowe zmienne losowe (X,Y)
Jest zmienną losową typu ciągłego, jeśli istnieje taka nieujemna funkcja f(x,y), że dla dowolnej pary (x,y) liczb rzeczywistych zachodzi równość:
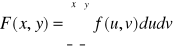
gdzie F(x,y) nazywamy dystrybuantą dwuwymiarowej zmiennej losowej typu ciągłego.
Funkcja f nosi nazwę gęstości dwuwymiarowej zmiennej losowej.
Gęstością dwuwymiarowej zmiennej losowej (X,Y) jest funkcja f(x,y) nieujemna spełniająca warunek:
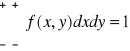
![]()
(nieujemna)
Jeżeli funkcja f jest ciągła w punkcie (x,y) to:
![]()
(druga pochodna dystrybuanty)
UWAGA
![]()
(X,Y)- dwuwymiarowa zmiennej losowej typu ciągłego
Rozkłady brzegowe
Jeżeli f(x,y) jest dystrybuantą dwuwymiarowej zmiennej losowej (x,y) to:
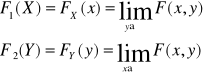
są funkcjami jednej zmiennej (odpowiednio zmiennej x lub y) nazywanymi dystrybuantami brzegowymi, a wyznaczone przez nie rozkłady, rozkładami brzegowymi.
Rozkłady brzegowe dwuwymiarowej zmiennej losowej typu skokowego
1). Niech (X,Y) jest dwuwymiarową zmienną losową typu skokowego przyjmującą wartości (xi,yk) z prawdopodobieństwem Pik
Oznaczamy:
![]()
![]()
Liczby ![]()
(![]()
) wyznaczają prawdopodobieństwo zmiennej losowej X(Y).Nazywamy ją rozkładem brzegowym zmiennej X (Y) w dwuwymiarowej zmiennej losowej (X,Y)
UWAGA:
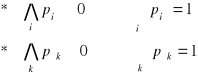
Rozkłady brzegowe dwuwymiarowej zmiennej losowej typu ciągłego
2. Niech (X,Y) jest dwuwymiarową zmienną losową o gęstości f(x,y).
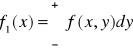
f1 - gęstość zmiennej losowej X. Nazywamy ją gęstością rozkładu brzegowego zmiennej X. ![]()
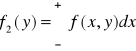
f2 - gęstość zmiennej losowej Y. Nazywamy ją gęstością rozkładu brzegowego zmiennej Y. ![]()
Dystrybuanta rozkładu brzegowego zmiennej losowej
dla zmiennej losowej typu skokowego:
Niech (X,Y) jest dwuwymiarową zmienną losową typu skokowego.
Dystrybuanta rozkładu brzegowego zmiennej losowej X wyraża się wzorem:
![]()
![]()
Dystrybuanta rozkładu brzegowego zmiennej losowej Y wyraża się wzorem
![]()
![]()
dla zmiennej losowej typu ciągłego:
Niech (X,Y) jest dwuwymiarową zmienną losową typu ciągłego.
Dystrybuanta rozkładu brzegowego zmiennej losowej X wyraża się wzorem:
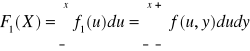
Dystrybuanta rozkładu brzegowego zmiennej losowej Y wyraża się wzorem:
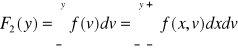
UWAGA:
- jeżeli X jest punktem ciągłości f1 to pochodna tej funkcji ![]()
- jeżeli Y jest punktem ciągłości f1 to ![]()
Niezależność zmiennych losowych
Zmienne X1, X2,…,Xn nazywamy zależnymi zmiennymi losowymi, jeżeli dla dowolnych zbiorów borelowskich A1, A2,…, An ![]()
zdarzenia ![]()
![]()
spełniają warunek:
![]()
iloczyn mnogościowy: ![]()
iloczyn zwykły: ![]()
Definicja
Zmienne X1,X2,… nazywamy niezależnymi zmiennymi losowymi, jeżeli dla każdego n zmienne X1,X2,…,Xn są niezależne.
Twierdzenie
1) dla niezależnych zmiennych losowych X1,X2,…,Xn zachodzi:
![]()
Szczególny przypadek dla n=2 dla niezależnych zmiennych losowych X,Y zachodzi
![]()
2) niezależnych zmiennych losowych X1,X2,…,Xn typu ciągłego zachodzi:
![]()
Szczególny przypadek dla n=2 dla niezależnych zmiennych losowych X,Y typu ciągłego zachodzi
![]()
3) niezależnych zmiennych losowych X1,X2,…,Xn typu skokowego zachodzi
![]()
Szczególny przypadek dla n=2 dla niezależnych zmiennych losowych X,Y typu skokowego zachodzi
![]()
Warunkowy rozkład prawdopodobieństwa zmiennych losowych
Niech (Ω,FP) jest przestrzenią probabilistyczną. X jest zmienną losową określoną na tej przestrzeni i![]()
Warunkowym rozkładem zmiennej losowej X pod warunkiem B nazywamy funkcję argumentu A oznaczoną Px (A/B) określoną wzorem:
![]()
1). Warunkowy rozkład prawdopodobieństwa dla zmiennej losowej typu skokowego:
Niech (X,Y) jest dwuwymiarową zmienną losową typu skokowego. Warunkowy rozkład prawdopodobieństwa zmiennej losowej X pod warunkiem, że zmienna losowa Y przyjmuje wartości yk (Y= yk) jest rozkładem określonym wzorem:
![]()
przy założeniu że: ![]()
Warunkowy rozkład prawdopodobieństwa zmiennej losowej Y pod warunkiem, że zmienna losowa X=xi jest rozkładem określonym wzorem:
![]()
przy założeniu, że ![]()
2). Warunkowy rozkład prawdopodobieństwa dla zmiennej losowej typu ciągłego:
Niech (X,Y) jest dwuwymiarową zmienną losową typu ciągłego. Warunkowy rozkład prawdopodobieństwa zmiennej losowej X pod warunkiem, że zmienna losowa Y=y, wyraża się wzorem:
![]()
![]()
, c<y<d przy założeniu, że gęstość rozkładu brzegowego zmiennej Y skoncentrowana jest na przedziale (c,d)
Warunkowy rozkład prawdopodobieństwa zmiennej losowej Y pod warunkiem, że zmienna losowa X=x jest rozkładem określonym wzorem:
![]()
![]()
a<x<b przy założeniu jw. (a,b)
Dystrybuanta warunkowa (rozkładu warunkowego)
1). Niech (X,Y) jest dwuwymiarową zmienną losową typu skokowego.
Dystrybuanta rozkładu warunkowego zmiennej losowej X przy warunku, że zmienna losowa Y= yk wyraża się wzorem:
![]()
![]()
Dystrybuanta rozkładu warunkowego zmiennej losowej Y przy warunku, że zmienna losowa X=xi wyraża się wzorem:
![]()
![]()
2). Niech (X,Y) jest dwuwymiarową zmienną losową typu ciągłego.
Dystrybuanta rozkładu warunkowego zmiennej losowej X przy warunku, że zmienna losowa Y= y wyraża się wzorem:
![]()
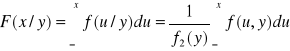
Dystrybuanta rozkładu warunkowego zmiennej losowej Y przy warunku, że zmienna losowa X=x wyraża się wzorem:
![]()