4.6. Interpolacja trygonometryczna

W wielu zagadnieniach zachodzi potrzeba interpolacji danej funkcji okresowej

o okresie T. Po dokonaniu zamiany zmiennej niezależnej
otrzymujemy funkcję okresową

(4.43)

o okresie 2 π, którą wystarczy rozpatrywać bez zmniejszania ogólności rozważań.

Zadanie interpolacji trygonometrycznej polega na znalezieniu dla danej funkcji y wielomianu trygonometrycznego

(4.44)

zawierającego nieznanych parametrów, który w różnych punktach wewnątrz przedziału [0, 2 π] przyjmuje te same wartości co interpolowana funkcja.

Najbardziej istotny w praktyce jest przypadek węzłów równoodległych, dobranych w następujący sposób

(4.45)

czyli:

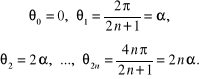
Biorąc pod uwagę własności sum zawierających iloczyny funkcji oraz dla kątów (4.45):

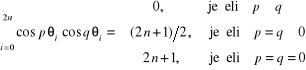
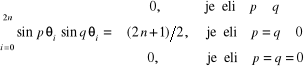
możemy łatwo stwierdzić, że macierz

(4.46)

gdzie

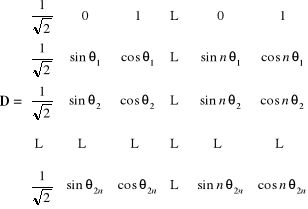
(4.47)

jest macierzą ortogonalną. Zatem układ równań liniowych dla nieznanych parametrów wielomianu trygonometrycznego (4.44)

(4.48)

w którym:

można rozwiązać w taki sam sposób jak układ równań dla współczynników optymalnego wielomianu interpolacyjnego

(4.49)

sprowadzający się do pomnożenia transponowanej macierzy (4.47) przez wektor Y, zawierający wartości funkcji w węzłach interpolacji (4.45).

Obliczanie współczynników wielomianu trygonometrycznego (4.44) według wzoru (4.49) dla podziału równoodległego (4.45) odbywa się w programie 4.4, którego tabulogram jest następujący:

{Program 4.4}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons, OleCtnrs;

type

Tabl1 = array[0..100] of Real;

Tabl2 = array[1..1000] of Real;

Tabl3 = array[0..50,0..50] of Real;

. . . . . . . . . . . . . . . . . . .

var

Form3: TForm3;

i,j,K,n,nn,n1,m,m1,X0,Y0,ZX,ZY: Integer;

a,al,b,bl,h,sum,th,x,y: Real;

af,bf,ck,sk,xw,yw: Tabl1;

xx,yy,Xekr,Yekr: Tabl2;

plik,plik1: Text;

mac,mac1: Tabl3;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

function f(x: Real): Real;

begin

if Form3.RadioButton1.Checked then

f:=100*x*x*Exp(-10*x);

if Form3.RadioButton2.Checked then

f:=1/(1+25*x*x);

if Form3.RadioButton3.Checked then

f:=16*x*x*(x-1)*(x-1);

end;

procedure fsico(k: Integer; x: Real; var ck,sk: Tabl1);

var

i: Integer;

co,si: Real;

label kon;

begin

co:=Cos(x); si:=Sin(x);

ck[0]:=1; sk[0]:=0;

if k=0 then goto kon;

for i:=1 to k do begin

ck[i]:=co*ck[i-1]-si*sk[i-1];

sk[i]:=si*ck[i-1]+co*sk[i-1];

end;

kon:

end;

. . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

AssignFile(plik,Edit6.Text);

AssignFile(plik1,Edit5.Text);

Rewrite(plik); Rewrite(plik1);

a:=StrtoFloat(Edit1.Text); b:=StrtoFloat(Edit2.Text);

n:=StrtoInt(Edit3.Text); m:=StrtoInt(Edit4.Text);

Writeln(plik,'PROGRAM 4.4.');

Writeln(plik,'Interpolacja trygonometryczna funkcji jednej zmiennej.');

Writeln(plik,'Początek przedziału: a = ',a:13);

Writeln(plik,'Koniec przedziału: b = ',b:13);

Writeln(plik,'Stopień wielomianu: n = ',n:3);

Writeln(plik,'Liczba punktów wykresu: m = ',m:3);

Writeln(plik); nn:=2*n; n1:=2*n+1;

m1:=2*m+1; h:=(b-a)/n1; al:=2*Pi/n1;

Writeln(plik1,n1:3); Writeln(plik1,nn:3);

Writeln(plik1,m1:3);

for i:=0 to n1 do begin

x:=a+i*h; y:=f(x);

xw[i]:=x; yw[i]:=y;

xx[i+1]:=x; yy[i+1]:=y;

end;

for i:=0 to nn do

mac[i,0]:=1/Sqrt(2);

for i:=0 to nn do begin

th:=i*al;

fsico(n,th,ck,sk);

for j:=1 to n do begin

mac[i,2*(j-1)+1]:=sk[j];

mac[i,2*(j-1)+2]:=ck[j];

end;

end;

for i:=0 to nn do

for j:=0 to nn do

mac1[i,j]:=2*mac[j,i]/n1;

sum:=0;

for j:=0 to nn do

sum:=sum+mac1[0,j]*yw[j];

af[0]:=sum; bf[0]:=0;

for i:=1 to nn do begin

sum:=0;

for j:=0 to nn do

sum:=sum+mac1[i,j]*yw[j];

if Odd(i) then bf[(i+1) div 2]:=sum

else af[i div 2]:=sum;

end;

xx[nn+3]:=0; yy[nn+3]:=0; K:=nn+3;

Writeln(plik,'Wyniki interpolacji funkcji:');

Writeln(plik,' i x[i] y[i] błąd');

h:=(b-a)/m1; al:=2*Pi/m1;

for i:=0 to m1 do begin

x:=a+i*h; th:=i*al;

fsico(n,th,ck,sk);

y:=af[0]/Sqrt(2);

for j:=1 to n do

y:=y+af[j]*ck[j]+bf[j]*sk[j];

bl:=f(x)-y;

Writeln(plik,i:3,' ',x:13,' ',y:16,' ',bl:13);

K:=K+1; xx[K]:=x; yy[K]:=y;

end;

for i:=1 to m1+n1+3 do

Writeln(plik1,xx[i]:13,' ',yy[i]:13);

CloseFile(plik); CloseFile(plik1);

Form2.Wyniki.Lines.LoadFromFile(Edit6.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

W programie 4.4 występuje procedura o nazwie fsico przeznaczona do obliczania funkcji trygonometrycznych i ze wzorów:

dla znanych wartości oraz

Na rysunkach 4.10 ÷ 4.12 przedstawione zostały wielomiany trygonometryczne uzyskane dla n = 5 za pomocą programu 4.4 dla trzech funkcji, odpowiednio, (4.20) w przedziale , (4.32) w przedziale [−1, 1] oraz

(4.50)

w przedziale Na wykresie wielomianu trygonometrycznego funkcji (4.20) (rys. 4.10) wystąpiły duże oscylacje przy końcu przedziału, gdyż zarówno funkcja ta jak i jej pochodne nie są funkcjami okresowymi.

Rys. 4.10

Rys. 4.11

Rys. 4.12

192 4. Interpolacja

4.6. Interpolacja trygonometryczna 193

---