Rozdział 3

RÓWNANIA NIELINIOWE

3.1. Wstęp

Zagadnienie wyznaczania pierwiastków równań nieliniowych, występujące często w różnych dziedzinach nauki i techniki, jest jednym z najstarszych zadań matematycznych. Przykładem takiego zagadnienia jest rozwiązywanie powszechnie znanego równania kwadratowego

którego pierwiastkami są liczby

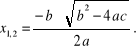
Dla funkcji
określonej w przedziale pojedyncze równanie nieliniowe możemy zapisać w postaci

(3.1)

Funkcja
może być algebraiczną funkcją nieliniową lub też funkcją przestępną.

Każdą wartość dla której funkcja przyjmuje wartość zero

(3.2)

nazywamy pierwiastkiem równania (3.1) lub zerem funkcji

W ogólnym przypadku dla dowolnej postaci funkcji nie istnieją metody dokładne rozwiązywania równań nieliniowych np. dla równań algebraicznych metody takie nie istnieją dla równań stopnia wyższego niż czwarty. Dlatego też w praktyce stosowane są różnego rodzaju metody iteracyjne, umożliwiające otrzymanie rozwiązań przybliżonych.

Większość metod przybliżonego rozwiązywania równań nieliniowych można stosować jedynie wtedy, gdy znamy przedział izolacji pierwiastka tzn. przedział,
w którym znajduje się pojedynczy pierwiastek rozwiązywanego równania. Istnieje wiele metod lokalizowania pierwiastków rzeczywistych. Najprostsze z nich to:

1) metoda graficzna - stosowana wtedy, gdy równanie wyjściowe (3.1) można przekształcić do postaci równoważnej

(3.3)

w której wykresy funkcji i są łatwiejsze do wykonania; pierwiastkami (3.2) równania (3.1) będą odcięte punktów przecięcia tych wykresów np. w przypadku równania

2) metoda tablicowania funkcji w przedziale jej określoności w m równoodległych punktach

(i = 1, 2, ..., m) (3.4)

z krokiem

.

Metody iteracyjne, pozwalające na obliczanie pierwiastków z żądaną dokładnością można podzielić na:

a) metody jednopunktowe, gdy następne przybliżenie pierwiastka zależy tylko od informacji obliczanej w jednym punkcie poprzednim,

b) metody wielopunktowe, gdy przy wyznaczaniu następnego przybliżenia pier-wiastka wykorzystuje się kilka jego przybliżeń, obliczanych w kilku punktach poprzednich.

Podstawowym warunkiem, jaki musi spełniać każda metoda iteracyjna jest zbieżność ciągu kolejnych przybliżeń: do pierwiastka równania
Każdej metodzie iteracyjnej można przyporządkować liczbę p, zwaną rzędem metody lub wykładnikiem zbieżności oraz stałą K, zwaną stałą asymptotyczną błędu metody - takie, że zachodzi nierówność

(3.5)

Rząd metody p i stała K charakteryzują szybkość zbieżności metody iteracyjnej: ciąg kolejnych przybliżeń: jest tym szybciej zbieżny do pierwiastka, im większy jest rząd metody i im mniejsza jest stała asymptotyczna błędu, najistotniejszą rolę gra jednak wykładnik zbieżności p.

Uogólniając pojedyncze równanie nieliniowe (3.1) otrzymamy układ n równań nieliniowych:

(3.6)

z n niewiadomymi , w którym symbole oznaczają znane rzeczywiste funkcje niewiadomych.

Układ równań (3.6) można zapisać w zwięzłej postaci wektorowej

(3.7)

po wprowadzeniu kolumnowego wektora niewiadomych

(3.8)

oraz kolumnowego wektora operatorowego

(3.9)

Do rozwiązania układu równań (3.7) najczęściej wykorzystywane są metody, stanowiące uogólnienie odpowiednich metod dla pojedynczego równania. Istnieje również pewna grupa metod oparta na minimalizacji funkcji, będącej sumą kwadratów lewych stron układu równań (3.6)

(3.10)

funkcja
osiąga minimum równe zeru w punkcie identycznym z rozwiązaniem układu równań (3.6).

Oprócz tych dwu grup metod istnieją również inne, które mogą okazać się bar-dziej skuteczne lub bardziej wygodne w przypadku układów równań nieliniowych
o szczególnych postaciach np. metoda parametru, która polega na wprowadzeniu do układu równań (3.7) pewnego parametru λ

(3.11a)

126 3. Równania nieliniowe

3.1. Wstęp 127

---