4.5. Interpolacja Czebyszewa

Wielomiany Czebyszewa są określone w przedziale związkiem rekurencyjnym:

(4.34)

wynikającym z tożsamości trygonometrycznej

(4.35)

po przyjęciu

Związek rekurencyjny (4.34) określa wielomiany parzyste, gdy n jest liczbą parzystą i wielomiany nieparzyste, gdy n jest liczbą nieparzystą. Oto kilka pierwszych wielomianów Czebyszewa:

Biorąc bazę Czebyszewa: jako układ funkcji liniowo niezależnych (4.6) otrzymamy wielomian interpolacyjny Czebyszewa

(4.36)

którego współczynniki są rozwiązaniem układu równań liniowych

(4.37)

gdzie:

,

Jeśli mamy do czynienia ze zmienną
przebiegającą dowolny przedział [a, b], to należy wykonać podstawienie

(4.38)

gdyż

Interpolacja Czebyszewa przy dowolnym wyborze węzłów interpolacji jest efektywna w tym sensie, że błędy zaokrągleń występujące przy rozwiązywaniu układu równań liniowych (4.37) są istotnie mniejsze w porównaniu z błędami zaokrągleń powstającymi przy rozwiązywaniu układu równań (4.5) dla interpolacji wielomianami w postaci naturalnej.

Druga bardzo ważna własność interpolacji Czebyszewa ujawnia się przy odpowiednim doborze węzłów interpolacji, będących zerami kolejnych wielomianów Czebyszewa (4.34)

(4.39)

Węzły interpolacji określone wzorem (4.39) nie są rozmieszczone w równych odstępach, lecz są zagęszczone przy końcach przedziału.

Z zasady minimaksu [3, 17] wynika, że ze wszystkich wielomianów n-tego stopnia (4.13) ze współczynnikiem wiodącym 1 najmniejszą normę maksymalną w przedziale
ma wielomian
jego norma maksymalna jest równa
Przyjęcie węzłów zgodnie z (4.39) gwarantuje więc tym samym uzyskanie minimalnego błędu interpolacji (4.33) w przedziale, w którym będzie użyty wzór interpolacyjny. Wielomian interpolacyjny rozpięty na węzłach (4.39), które są pierwiastkami wielomianu Czebyszewa nazywa się optymalnym wielomianem interpolacyjnym.

Jeżeli jako węzły interpolacji przyjmiemy węzły Czebyszewa (4.39) - to z jednej strony otrzymamy pewną minimalizację błędu interpolacji, a z drugiej strony z własności wielomianów Czebyszewa:

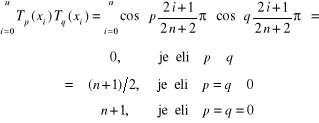
(4.40)

wynika, że dla

(4.41)

macierz współczynników układu równań (4.37) pomnożona przez stałą jest macierzą ortogonalną (2.30)

Zatem jest

(4.42)

co stanowi bardzo istotne uproszczenie obliczeń.

{Program 4.3}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons, ExtCtrls, OleCtnrs;

const nmax = 20;

type

Tabl1 = array[0..100] of Real;

Tabl2 = array[1..1000] of Real;

Tabl3 = array[0..nmax,0..nmax+1] of Real;

. . . . . . . . . . . . . . . . . . . . . .

var

Form3: TForm3;

i,j,K,n,m,wez,X0,Y0,ZX,ZY: Integer;

a,b,bl,det,h,t,x,y: Real;

xx,yy,Xekr,Yekr: Tabl2;

plik,plik1: Text;

acz,xw,yw: Tabl1;

mac,mac1: Tabl3;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

function f(x: Real): Real;

begin

if Form3.RadioButton1.Checked then

f:=100*x*x*Exp(-10*x);

if Form3.RadioButton2.Checked then

f:=1/(1+25*x*x);

end;

function WielCzeb(n: Integer; x: Real): Real;

var

k: Integer;

Tn,Tn1,Tn2: Real;

label kon;

begin

Tn2:=1; Tn1:=x;

if n=0 then begin

Tn:=Tn2; goto kon;

end;

if n=1 then begin

Tn:=Tn1; goto kon;

end;

for k:=2 to n do begin

Tn:=2*x*Tn1-Tn2;

Tn2:=Tn1; Tn1:=Tn;

end;

kon:

WielCzeb:=Tn;

end;

{procedure ElimGaussa0(n,m: Integer; var A: Tabl3; var det: Real);}

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

AssignFile(plik,Edit6.Text);

AssignFile(plik1,Edit5.Text);

Rewrite(plik); Rewrite(plik1);

Writeln(plik,'PROGRAM 4.3.');

if RadioButton3.Checked then wez:=1;

if RadioButton4.Checked then wez:=2;

a:=StrtoFloat(Edit1.Text); b:=StrtoFloat(Edit2.Text);

n:=StrtoInt(Edit3.Text); m:=StrtoInt(Edit4.Text);

Writeln(plik,'Interpolacja Czebyszewa funkcji jednej zmiennej.');

case wez of

1: Writeln(plik,'Węzły interpolacji rozłożone równomiernie.');

2: Writeln(plik,'Węzły interpolacji są węzłami Czebyszewa.');

end;

Writeln(plik);

Writeln(plik,'Początek przedziału: a = ',a:13);

Writeln(plik,'Koniec przedziału: b = ',b:13);

Writeln(plik,'Liczba węzłów: n = ',n:3);

Writeln(plik,'Liczba punktów wykresu: m = ',m:3);

Writeln(plik1,n:3); Writeln(plik1,m:3);

Writeln(plik);

h:=(b-a)/n;

if wez=1 then begin

for i:=0 to n do begin

x:=a+i*h; y:=f(x);

xw[i]:=x; yw[i]:=y;

xx[i+1]:=x; yy[i+1]:=y;

end;

for i:=0 to n do begin

mac[i,0]:=1/Sqrt(2);

mac[i,n+1]:=yw[i];

for j:=1 to n do begin

t:=2*xw[i]/(b-a)-(a+b)/(b-a);

mac[i,j]:=WielCzeb(j,t);

end;

end;

ElimGaussa0(n,1,mac,det);

for i:=0 to n do

acz[i]:=mac[i,n+1];

end;

if wez=2 then begin

for i:=0 to n do begin

t:=Cos((2*i+1)*Pi/(2*n+2));

x:=0.5*(a+b)+0.5*(b-a)*t;

y:=f(x); xw[i]:=x; yw[i]:=y;

xx[i+1]:=x; yy[i+1]:=y;

end;

for i:=0 to n do begin

mac[i,0]:=1/Sqrt(2);

mac[i,n+1]:=yw[i];

for j:=1 to n do begin

t:=2*xw[i]/(b-a)-(a+b)/(b-a);

mac[i,j]:=WielCzeb(j,t);

end;

end;

for i:=0 to n do

for j:=0 to n do

mac1[i,j]:=2*mac[j,i]/(n+1);

for i:=0 to n do begin

t:=0;

for j:=0 to n do

t:=t+mac1[i,j]*yw[j];

acz[i]:=t;

end;

end;

xx[n+2]:=0; yy[n+2]:=0; K:=n+2;

Writeln(plik,'Wyniki interpolacji funkcji:');

Writeln(plik,' i x[i] y[i] błąd');

h:=(b-a)/m;

for i:=0 to m do begin

x:=a+i*h;

t:=2*x/(b-a)-(a+b)/(b-a);

y:=acz[0]/Sqrt(2);

for j:=1 to n do

y:=y+acz[j]*WielCzeb(j,t);

bl:=f(x)-y;

Writeln(plik,i:3,' ',x:13,' ',y:16,' ',bl:13);

K:=K+1; xx[K]:=x; yy[K]:=y;

end;

for i:=1 to m+n+3 do

Writeln(plik1,xx[i]:13,' ',yy[i]:13);

CloseFile(plik); CloseFile(plik1);

Form2.Wyniki.Lines.LoadFromFile(Edit6.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

W programie 4.3 procedura funkcyjna WielCzeb jest przeznaczona do obliczania wartości wielomianu Czebyszewa (4.34) dla zadanej wartości argumentu w przedziale , a procedura ElimGaussa0 jest zmodyfikowaną procedurą Elim-Gaussa - przystosowaną do rozwiązywania układu algebraicznych równań liniowych metodą eliminacji Gaussa, numerowanych od zera. Program ten jest przeznaczony do interpolacji funkcji jednej zmiennej w dowolnym przedziale
dla dwóch wariantów obliczeń, przy przyjęciu:

1) równomiernego odstępu między węzłami interpolacji,

2) jako węzłów interpolacji węzłów Czebyszewa (4.39).

Za pomocą programu 4.3 powtórzono obliczenia dla przykładu Runge'go (4.32). Oczywiście przy wyborze pierwszego wariantu obliczeń otrzymujemy takie same wielomiany interpolacyjne, jakie są pokazane na rysunkach 4.3 ÷ 4.5. Natomiast przy wyborze drugiego wariantu obliczeń występuje istotne ograniczenie błędów interpolacji przy końcach przedziału, dla dużych n, co zostało uwidocznione na rysunkach 4.6 ÷ 4.9, uzyskanych również dla n = 4, 7 i 10 oraz dodatkowo n = 15.

Rys. 4.6

Rys. 4.7

Rys. 4.8

Rys. 4.9

186 4. Interpolacja

4.5. Interpolacja Czebyszewa 187

---