(5.60)

przy czym współrzędne punktów Gaussa oraz wagi są takie same jak dla całek pojedynczych, np. dla mamy

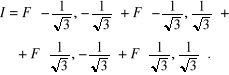
W podobny sposób stosowane są kubatury Gaussa do obliczania całek potrójnych w znormalizowanym czworościanie i znormalizowanym sześcianie [24].

5.3. Rodzaje aproksymacji

Aproksymacja jest działem analizy numerycznej zajmującym się najbardziej ogólnymi zagadnieniami przybliżania funkcji, polegającymi na wyznaczaniu dla danej funkcji
takich funkcji F(x), które w określonym sensie najlepiej przybliżają funkcję
.

Potrzeba przybliżania danej funkcji inną funkcją pojawia się w wielu zadaniach. Może mieć np. zastosowanie przy obliczaniu funkcji standardowych lub wtedy, gdy funkcja
jest zdefiniowana bardzo skomplikowanym wzorem. Jednym ze sposobów rozwiązania tego zadania jest przybliżanie funkcji
sumami częściowymi ich rozwinięć w szeregi Taylora - przykładami mogą być tu przedstawione w rozdziałach 1.6 i 1.7 algorytmy obliczania wartości funkcji elementarnych.

Zadania aproksymacyjne mogą być formułowane bardzo różnie, w zależności od przyjętego sposobu oszacowania błędów aproksymacji. Wyróżnia się trzy rodzaje aproksymacji:

1) interpolacyjną,

2) jednostajną,

3) średniokwadratową.

W przypadku aproksymacji interpolacyjnej, podobnie jak w zagadnieniu interpolacji, żądamy spełnienia warunku, aby funkcja dana
i funkcja szukana przyjmowały dokładnie te same wartości na zbiorze z góry ustalonych punktów węzłowych (rys. 5.6). Warunek ten może być uzupełniony warunkami wyrażającymi równość pochodnych w węzłach, jeżeli wartości pochodnych zostaną zadane.

Rys. 5.6

Rys. 5.7

W przypadku aproksymacji jednostajnej funkcję
przybliżamy taką funkcją która daje najmniejsze maksimum różnicy między a
w całym przedziale [a, b] - rys. 5.7

(5.61)

Twierdzenie Weierstrassa (rozdz. 4.4) gwarantuje, że zawsze można znaleźć wielomian o dowolnie małym odchyleniu od funkcji
na przedziale [a, b]. Nie ma jednak ogólnej metody umożliwiającej znajdowanie wielomianu najlepszego przybliżenia jednostajnego stopnia n dla dowolnej funkcji ciągłej na [a, b].

Jedną z metod aproksymacji jednostajnej jest metoda szeregów potęgowych. Z punktu widzenia możliwości i wykorzystania maszyn cyfrowych do aproksymacji jednostajnej wielu funkcji bardzo przydatne okazały się - rozważane już wcześniej w rozdziale 1.6 - przybliżenia wymierne

gdzie i są elementami tej samej bazy, a i - stałymi współczynnikami. Do budowania przybliżeń wymiernych wykorzystywane są wielomiany potęgowe (przybliżenia Padego) oraz wielomiany Czebyszewa (4.34) [1, 9].

Rys. 5.8

W przypadku aproksymacji średniokwadratowej jako miarę odchylenia funkcji od danej funkcji
przyjmujemy wielkość

(5.62)

zwaną odchyleniem kwadratowym. Funkcja aproksymująca wyznaczana jest z warunku, aby wartość wyrażenia (5.62) była możliwie najmniejsza. Geometrycznie warunek ten wyraża żądanie, aby pole powierzchni między liniami reprezentującymi funkcję
oraz funkcję było minimalne. Jest to pole zakreskowane na ry-sunku 5.8.

286 5. Różniczkowanie, całkowanie i aproksymacja

5.3. Rodzaje aproksymacji 287

---