x1:=x; fx1:=fx;

iter:=iter+1;

until (bl<eps) or (Abs(fx)<eps);

Writeln(plik,'Pierwiastek równania - ksi = ',x:18);

Writeln(plik,'Residuum równania: f(ksi) = ',fx:11);

Writeln(plik,'Liczba iteracji: ',iter);

omin:

CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(Edit4.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

Program 3.4 jest przeznaczony do rozwiązywania równania (3.18) metodą siecznych po wczytaniu dwóch początkowych przybliżeń pierwiastka: , oraz dokładności obliczeń ε .

Tabulogramy wyników uzyskanych dla dwóch zestawów danych są następujące:

PROGRAM 3.4.

Rozwiązywanie równania nieliniowego:

f(x) = x - sin(x) - 0.25 = 0.

Metoda siecznych.

Przybliżenia początkowe:

x0 = 5.0E-0001

x1 = 7.0E-0001

f(x0) = -2.294255386E-0001

f(x1) = -1.942176872E-0001

Dokładność obliczeń - eps = 1.0E-0009

Pierwiastek równania - ksi = 1.171229653E+0000

Residuum równania: f(ksi) = 2.08E-0013

Liczba iteracji: 8

PROGRAM 3.4.

Rozwiązywanie równania nieliniowego:

f(x) = x - sin(x) - 0.25 = 0.

Metoda siecznych.

Przybliżenia początkowe:

x0 = 1.0E+0000

x1 = 1.5E+0000

f(x0) = -9.147098481E-0002

f(x1) = 2.525050134E-0001

Dokładność obliczeń - eps = 1.0E-0009

Pierwiastek równania - ksi = 1.171229652E+0000

Residuum równania: f(ksi) = -1.56E-0010

Liczba iteracji: 5

3.4. Metody Newtona dla układów równań

Wszystkie skalarne metody iteracyjne rozwiązania pojedynczego równania nieliniowego (3.1) dają się teoretycznie rozszerzyć na przypadek układu równań nieliniowych (3.6). W niniejszym rozdziale ograniczymy się do przedstawienia najczęściej wykorzystywanych w praktyce uogólnień klasycznej i zmodyfikowanej metody Newtona. Uogólnienie innych metod np. metody bisekcji czy metody regula falsi jest znacznie bardziej skomplikowane, gdyż dla niezawodnego działania tych metod niezbędne jest określenie przedziału izolacji pierwiastka, który należałoby odnieść do przestrzeni wielowymiarowej.

Metody iteracyjne Newtona (3.19) i (3.24) można uogólnić korzystając z pojęcia różniczki zupełnej każdej z funkcji występującej w układzie równań (3.6). Zakładając, że znamy k-te przybliżenie

(3.32)

każdego z pierwiastków, nie spełniające na ogół równania wektorowego (3.7), ot-rzymujemy residuum

(3.33)

gdzie

Po obliczeniu różniczek zupełnych każdej z funkcji

i dobraniu ich wartości tak, aby zniwelować błędy k-tego przybliżenia

uzyskujemy następujący układ równań

(3.34)

w którym różniczki zupełne zostały zastąpione różnicami skończonymi

(3.35)

a symbol oznacza wartość odpowiedniej pochodnej cząstkowej w punkcie odpowiadającym k-temu przybliżeniu.

Wprowadzając macierz Jacobiego dla układu funkcji względem zmiennych

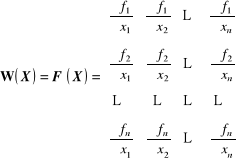
, (3.36)

możemy układ równań liniowych (3.34) ostatecznie zapisać w następującej postaci macierzowej

(3.37)

określającej ciąg kolejnych przybliżeń klasycznej metody Newtona.

Wobec faktu szybkiej lokalnej zbieżności i prostej formuły (3.37) obliczania kolejnych przybliżeń rozwiązywania układu (3.7) metoda Newtona znalazła szerokie zastosowanie w obliczeniach na maszynach cyfrowych. W przypadku, gdy liczba zmiennych n jest duża istotną trudność może stanowić operacja odwracania macierzy Jacobiego oraz samo wyznaczanie pochodnych (3.36). Wówczas zamiast układu równań liniowych (3.37) dla składowych wektora można:

1) rozwiązywać równoważny układ równań liniowych dla przyrostów wektora niewiadomych

(3.38)

2) zastosować zmodyfikowaną metodę Newtona (3.24) do ciągu kolejnych przybliżeń (3.37)

(3.39)

lub też ciągu kolejnych przybliżeń (3.38),

3) zastąpić pochodne (3.36) ich przybliżeniami różnicowymi

(3.40)

w których jest zadanym, dostatecznie małym przyrostem zmiennej

Rozwiązywanie układu równań nieliniowych (3.7) przy wykorzystaniu klasycznej metody Newtona (3.37) odbywa się w programie 3.5, w którym wykorzystano procedurę (2.58) rozwiązywania układu równań liniowych metodą eliminacji Gaussa. Funkcje oraz elementy macierzy Jacobiego (3.36) obliczane są w procedurach funkcyjnych F(i,X) oraz W(i,j,X).

Tabulogram modułu Obliczenia programu 3.5 przedstawia się następująco:

{Program 3.5}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

const nmax = 20;

type

Wektor = array[1..nmax] of Real;

Tabl = array[1..nmax,1..2*nmax] of Real;

. . . . . . . . . . . . . . . . . . . . .

var

Form3: TForm3;

i,j,k,n,iter,licz: Integer;

bl,det,eps,sp: Real;

zbior: String;

plik: Text;

X: Wektor;

A: Tabl;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

{procedure ElimGaussa(n,m: Integer; var A: Tabl; var det: Real);}

function F(i: Integer; X: Wektor): Real;

begin

case i of

1: F:=Sqr(X[1])+Sqr(X[2])+Sqr(X[3])-1;

2: F:=2*Sqr(X[1])+Sqr(X[2])-4*X[3];

3: F:=3*Sqr(X[1])-4*X[2]+Sqr(X[3]);

end;

end;

function W(i,j: Integer; X: Wektor): Real;

begin

case i of

1: W:=2*X[j];

2: case j of

1: W:=4*X[1];

2: W:=2*X[2];

3: W:=-4;

end;

3: case j of

1: W:=6*X[1];

2: W:=-4;

3: W:=2*X[3];

end;

end;

end;

. . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

AssignFile(plik,zbior);

Reset(plik);

Readln(plik,n,eps,iter);

for i:=1 to n do

Read(plik,X[i]);

CloseFile(plik);

AssignFile(plik,Edit1.Text);

Rewrite(plik); Writeln(plik,'PROGRAM 3.5.');

Writeln(plik,'Rozwiązywanie układu równań nieliniowych.');

Writeln(plik,'Metoda Newtona.'); Writeln(plik);

Writeln(plik,'Liczba równań układu - n = ',n:2);

Writeln(plik,'Zadana liczba iteracji - iter = ',iter:4);

Writeln(plik,'Zadana dokładność obliczeń - eps = ',eps:13);

Writeln(plik);

Writeln(plik,'Przybliżenie początkowe:');

Write(plik,' '); k:=0;

for i:=1 to n do begin

k:=k+1;

if k=5 then begin

k:=0; Writeln(plik);

Write(plik,' ');

end;

Write(plik,' ',X[i]:13);

end;

Writeln(plik);

licz:=0;

repeat

bl:=0;

licz:=licz+1;

for i:=1 to n do

for j:=1 to n do begin

A[i,j]:=W(i,j,X);

if i=j then A[i,n+j]:=1

else A[i,n+j]:=0;

end;

ElimGaussa(n,n,A,det);

for i:=1 to n do begin

sp:=0;

for j:=1 to n do

sp:=sp+A[i,n+j]*F(j,X);

if Abs(sp)>bl then bl:=Abs(sp);

X[i]:=X[i]-sp;

end;

until (bl<eps) or (licz=iter);

Writeln(plik);

Writeln(plik,'Liczba wykonanych iteracji: ',licz:3);

Writeln(plik);

Writeln(plik,'Rozwiązanie układu równań:');

Write(plik,' '); k:=0;

for i:=1 to n do begin

k:=k+1;

if k=5 then begin

k:=0; Writeln(plik);

Write(plik,' ');

end;

Write(plik,' ',X[i]:16);

end;

Writeln(plik); Writeln(plik);

Writeln(plik,'Residua równań:');

Write(plik,' '); k:=0;

for i:=1 to n do begin

k:=k+1;

if k=5 then begin

k:=0; Writeln(plik);

Write(plik,' ');

end;

Write(plik,' ',F(i,X):13);

end;

Writeln(plik); CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(Edit1.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn4Click(Sender: TObject);

begin

Close;

end;

end.

Dane do programu 3.5, zapisywane w zbiorze Pr_3_5.dan, składają się z następujących elementów:

n - liczba równań w układzie,

148 3. Równania nieliniowe

3.4. Metody Newtona dla układów równań 149

---