4. Norma spektralna. Jest określana jako pierwiastek z promienia spektralnego (2.14) iloczynu macierzy A oraz jej macierzy transponowanej

(2.34)

2.2. Ogólna charakterystyka metod. Uwarunkowanie zadania

Będziemy zajmować się metodami rozwiązywania układu n algebraicznych równań liniowych z n niewiadomymi postaci:

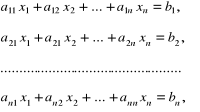
(2.35)

w którym poszczególne symbole oznaczają:

- zadane współczynniki,

- niewiadome,

- zadane wartości prawych stron (wyrazy wolne).

Układ równań (2.35) można zapisać w bardziej zwięzły sposób

(2.36)

wprowadzając macierz współczynników układu równań

wektor kolumnowy prawych stron

oraz wektor kolumnowy niewiadomych

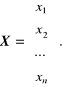
Układ równań liniowych nazywa się układem niejednorodnym, jeśli wektor prawych stron W przypadku natomiast układ równań nazywa się uk-ładem jednorodnym. Rozwiązanie zarówno układu niejednorodnego, jak i układu jednorodnego istnieje i jest jedyne, jeśli [4]

(2.37)

W tym przypadku układ jednorodny ma jedyne rozwiązanie zerowe, warunkiem istnienia niezerowego rozwiązania układu jednorodnego jest znikanie wyznacznika.

*

Metody rozwiązywania układów równań dzielimy na dwie podstawowe grupy:

1) metody dokładne (bezpośrednie),

2) metody iteracyjne.

Metody dokładne pozwalają uzyskać rozwiązanie po skończonej liczbie działań. Są to takie metody, które doprowadziłyby do otrzymania dokładnego rozwiązania układu, jeśli wszystkie działania byłyby wykonywane bez zaokrągleń; metody dokładne nie są więc obarczone błędem metody.

Najczęściej wykorzystywanymi w obliczeniach numerycznych metodami dokładnymi są: metoda eliminacji Gaussa i metoda Banachiewicza wraz z ich modyfikacjami. Do metod dokładnych należy też metoda oparta na odwróceniu macierzy współczynników oraz metoda wyznaczników Cramera.

W metodzie opartej na odwróceniu macierzy współczynników rozwiązanie układu (2.36), przy spełnieniu warunku (2.37), otrzymujemy po lewostronnym jego pomnożeniu przez macierz odwrotną

(2.38)

Zadanie odwracania macierzy sprowadza się jednak do rozwiązania n układów równań liniowych, niezbędnych do wyznaczenia niewiadomych elementów macierzy  Ten elegancki sposób jest więc bardzo czasochłonny (pomimo faktu, że rozwiązywanie tych układów równań odbywa się na ogół równocześnie) i może być zastosowany przy niezbyt dużej liczbie równań w układzie (2.36).

Metoda wyznaczników Cramera dla większej liczby równań ma znaczenie czysto teoretyczne ze względu na bardzo dużą liczbę operacji rachunkowych, niemożliwych do wykonania nawet za pomocą bardzo dużych komputerów. Już dla n = 14 metoda ta wymagałaby wykonania ok. mnożeń i tyleż dodawań. Maszyna wykonująca milion operacji arytmetycznych w ciągu 1 sek. obliczyłaby więc rozwiązanie dopiero po ośmiu miesiącach nieprzerwanej pracy [6].

Metody iteracyjne odznaczają się tym, że dostarczają ciągu rozwiązań przybliżonych, zbieżnych do rozwiązania ścisłego układu równań (2.36). Cechą charakterystyczną tych metod jest odpowiedni cykliczny algorytm, w którym na podstawie znajomości przybliżenia poprzedniego (niższego) obliczane jest przybliżenie następne (wyższe). Są one zbieżne do rozwiązania dokładnego tylko w granicy, stąd błąd metody jest więc prawie zawsze małą częścią błędu obliczonego rozwiązania układu równań (2.36).

Metody iteracyjne można przedstawić w ogólny sposób za pomocą dowolnej nieosobliwej macierzy C tworząc zależność

którą sprowadzamy do postaci

(2.39)

gdzie jest macierzą kwadratową, - wektorem kolumnowym.

Równanie (2.39) można wykorzystać do utworzenia ciągu kolejnych przybliżeń

(2.40)

dla znanego przybliżenia początkowego Proces iteracyjny jest zbieżny, jeżeli istnieje wektor graniczny

(2.41)

spełniający układ (2.36), niezależny od wyboru przybliżenia początkowego Jeśli macierze i są niezależne od numeru przybliżenia metodę iteracyjną nazywamy stacjonarną, jeśli są zależne od tego numeru - niestacjonarną.

Z nieskończenie wielu sposobów przekształcania równania (2.36) na równanie (2.39) użyteczne są tylko te, które pozwalają skonstruować zbieżne ciągi iteracyjne. Najbardziej znanymi metodami stacjonarnymi są:

- metoda Jacobiego (iteracji prostej),

- metoda Gaussa-Seidela,

- metody relaksacyjne,

- metoda Richardsona.

Spośród metod niestacjonarnych najbardziej popularnymi są:

- metoda kolejnej nadrelaksacji z niestacjonarną macierzą iteracyjną,

- metoda najszybszego spadku,

- metoda sprzężonych gradientów,

- metoda naprzemiennych kierunków.

Do rozwiązywania układów równań liniowych wysokiego stopnia stosuje się niemal wyłącznie metody iteracyjne, a to ze względu na mniejsze obciążenie pamięci i prostotę algorytmów w porównaniu z metodami dokładnymi. Metody iteracyjne są szczególnie często stosowane przy rozwiązywaniu układów równań z macierzami rzadkimi, za wyjątkiem układów równań z macierzami pasmowymi, które są rozwiązywane za pomocą specjalnych algorytmów, będących szczególnymi odmianami metod dokładnych. Pojęcie „małego” i „wielkiego” układu równań jest względne gdyż, dla dużych maszyn cyfrowych liczba równań rzędu kilkuset może być bowiem jeszcze uważana za małą.

*

Zbadamy obecnie uwarunkowanie zadania rozwiązywania układu równań liniowych badając wpływ zaburzeń danych na zaburzenie rozwiązania [7, 8].

Najpierw zbadamy wpływ zaburzeń prawej strony na zaburzenie rozwiązania. Mamy więc

stąd po wykorzystaniu równania (2.36) dostajemy zależność

Z zależności tej i z równania (2.36) wynikają nierówności:

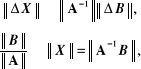
z których uzyskujemy oszacowanie błędu względnego rozwiązania, spowodowanego błędem względnym prawych stron

(2.42)

Wskaźnikiem (1.8) uwarunkowania układu równań liniowych ze względu na za-burzenia prawej strony jest więc wielkość

(2.43)

Zbadamy teraz wrażliwość rozwiązania na zaburzenie macierzy układu

(2.44)

przy wykorzystaniu dwóch tożsamości:

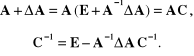
(2.45)

Z zależności (2.44), równania (2.36), pierwszej tożsamości (2.45) i własności macierzy odwrotnej dostajemy

(2.46)

Zważywszy, że z drugiej tożsamości (2.45) otrzymujemy nierówność

dla Ze związku (2.46) wynika zatem oszacowanie

które przy założeniu można przepisać w postaci następującej

(2.47)

Okazuje się więc, że wielkość - wyrażona wzorem (2.43) - charakteryzuje również wrażliwość rozwiązania na zaburzenia macierzy układu, gdyż na podstawie nierówności

(2.48)

stwierdzamy, że wskaźnik uwarunkowania macierzy jest zawsze liczbą nie mniejszą od jedności. Z porównania oszacowań (2.42) i (2.47) stwierdzamy ponadto, że błąd rozwiązania jest bardziej wrażliwy na błędy współczynników macierzy, niż na błędy prawych stron.

W rozdziale 1.2 jako przykład zadania źle uwarunkowanego rozważano układ równań określony macierzą współczynników

i różnymi wektorami prawych stron. Obliczymy wskaźnik uwarunkowania tej macierzy w normie (2.31). Macierz odwrotna jest następująca

58 2. Układy równań liniowych

2.2. Ogólna charakterystyka metod. Uwarunkowanie zadania 59

---