Zjawiska masowe to takie które powtarzają się często oraz badane w dużej masie wykazują określone prawidłowości.

Prawidłowości tych nie można dostrzec analizując pojedyncze przypadki.
Badania empiryczne opierają się na bezpośrednim, zmysłowym poznawaniu zjawisk i sytuacji. Badane zjawiska mogą mieć charakter zjawisk pojedynczych lub masowych. Do zjawisk pojedynczych zalicza się te, które są zupełnie jedynymi i niepowtarzalnymi zjawiskami. Zjawiska masowe natomiast to te, które występują wielokrotnie lub przynajmniej dwa razy. Czasopismo „Nowa Szkoła” jest zjawiskiem pojedynczym, natomiast czasopismo pedagogiczne należy do zjawisk masowych, ponieważ tylko na terenie Polski publikuje się ich kilkadziesiąt. Nauczycielka Anna Chmielewska z miasta R. jest zjawiskiem pojedynczym, natomiast nauczycielka wczesnej edukacji jest oczywiście zjawiskiem masowym.

STATYSTYKA-dyscyplina matematyczna zajmująca się metodami:

-Zbierania

-Opracowywania

-Analizy danych o zjawiskach masowych

STSTYSTYKA OPISOWA:

-Zajmuje się wstępnym opracowaniem próbki bez posługiwania się rachunkiem prawdopodobieństwa

-Metody i narzędzia statystyki opisowej nie upoważniają nas do wnioskowania statystycznego.

STATYSTYKA MATEMATYCZNA:

-Dyscyplina matematyczna zajmująca się metodami wnioskowania o całej zbiorowości statystycznej na podstawie zbudowania pewnej jej części zwanej próba,

-Metody statystyki (z powodu losowości próby) opierają się na metodach rachunku prawdopodobieństwa,

POPULACJA GENERALNA-zbiorowość statystyczna , zbiór ,którego elementy są przedmiotem budowania ze względu na określoną cechę X.

PRÓBA-podzbiór populacji generalnej podlegający bezpośredniemu badaniu ze wzg. Na ustalona cechę X.

PRÓBA LOSOWA- próba której dobór z całej populacji generalnej dokonuje się na zasadzie losowania i w sposób przypadkowy.

Pojęcia te różnią się tym że każde podlega pod siebie :próba losowa pod próbę a próba pod zbiorowość statystyczną .Mogą się różnić liczebnością, płcią lub innymi cechami populacji na której przeprowadza się próbę. Zbiorowość statystyczna jest bardzo ogólnym pojęciem i zawiera w sobie dwa następne. Cechą wspólną tych pojęć jest to że badaniu podlega pewna cecha X.

CECHA STATYSTYCZNA- właściwość jednostek statystycznych wchodzących w skład populacji generalnej.CECHY DZIELIMY NA:

1.Cechy stałe- określają jednostki pod wzg.:

-Czasowym

-Rzeczowym

-Przestrzennym

2.Cechy zmienne - właściwości, którymi różnią się poszczególne jednostki statystyczne

Badaniom statystycznym podlegają tylko cechy zmienne.

CECHY STAŁE:

-są wspólne dla wszystkich jednostek badanej zbiorowości statystycznej,

-nie podlegają badaniom statystycznym,

-decydują jedynie o zaliczeniu jednostek do określonych zbiorowości,

CECHY ZMIENNE:

1.mierzalne- zwane też ilościowymi np. długość , wytrzymałość, ciężar,

2.niemierzalne- zwane też jakościowymi np. kolor, płeć ,zawód,

Cechom mierzalnym można przypisać wartości liczbowe lub nadawać im tzw. rangi.

Po takim przyporządkowaniu cechę niemierzalną można traktować jak cechę mierzalną .

CECHY MIERZALNE:

1.skokowe- przyjmują wartości ze zbioru co najwyżej przeliczalnego,

2.ciągłe- przyjmują wartości z przedziału liczbowego,

POZYSKIWANIE DANYCH:

1.Sposoby pozyskiwania danych:

-Korzystane z publikowanych źródeł informacji-> GUS (roczniki statystyczne studiu i analizy i informacje i opracowania, materiały źródłowe,

-Publikacje instytucji i org. Pozarządowych

-Publikacje branż przemysłowych (czasopisma)

-Przeprowadzanie własnego badania statystycznego lub eksperymentu,

BADANIA SATYSTYCZNE to proces pozyskiwania danych na temat rozkładu ,cechy statystycznej w populacji.

Cel badania statystycznego- wyznaczanie wartości wybranych parametrów badanej zbiorowości jej analiza.

Realizacja tego celu:

-ustalenie przedmiotu i zakresu badań ,

-wybór odpowiedniej metody badawczej,

-wyznaczenie wartości wybranych parametrów,

-przeprowadzenie analizy zbiorowości na bazie otrzymanych wyników.

WYBÓR METODY BADAWCZEJ:

Czynniki natury statystycznej decydują o wyborze metody badawczej:

-cel badania,

-rodzaj zbiorowości statystycznej,

-tematyka badań,

-stopień szczególności badania,

Czynniki natury nie statystycznej wpływają na wybór metody badawczej:

-wielkości środków na badaniu,

-wielkości zespołu badawczego ,

-czas przeznaczony na badania,

ETAPY BADANIA STATYSTYCZNEGO. SZEREG ROZDZIELCZY

W każdym badaniu statystycznym można wyróżnić następujące etapy:

1.Etap I -przygotowanie badania

2.Etap II -obserwacja statystyczna

3.Etap III -opracowanie i prezentacja materiału statystycznego

4.Etap IV -opis lub wnioskowanie statystyczne

ETAP I

-Ustalenie celu

-Określenie przedmiotu badania -ustalenie zbiorowości statystycznej i jednostki badania pod wzg. rzeczowym (co badamy?), czasowym (kiedy?) i przestrzennym (gdzie?) oraz jednostki sprawozdawczej (te jednostki ,które posiadają źródła danych)

-Wybór metody badawczej

ETAP II

-Ustalenie wartości cech ilościowych lub odmian cech jakościowych

U wszystkich jednostek tworzących zbiorowość statystyczną lub prawidłowość dobranej próby.

Zbiór danych uzyskanych w wyniku obserwacji nazywamy materiałem statystycznym.

MATERIAŁ STATYSTYCZNY DZIELIMY NA:

-Materiał pierwotny - uzyskany ze specjalnie przeprowadzonego dla danego celu badania,

-Materiał wtórny - uzyskany ze źródeł gromadzonych do innych celów,

RODZAJE BŁĘDÓW jakimi obciążany jest materiał statystyczny:

1.Błędy statystyczne - są wynikiem jednokierunkowej tendencji do zniekształcania rzeczywistości (np. źle wyskalowanie narzędzie pomiarowe),

2.Błędy przypadkowe

ETAP III

-Gromadzenie

-Zliczanie

GROMADZENIE MATERIAŁU STATYSTYCZNEGO-polega na utworzeniu odpowiednich grup (klas, przedziałów klasowych) , przy uwzględnieniu następujących czynników:

-Stopień dokładności pomiaru

-Liczebność badanej zbiorowości lub próby,

-Cel i zakres badań,

-Rodzaj badanej cechy(skokowy czy ciągły),

-Obszar zmienności cechy

Grupowanie może mieć charakter naturalny np. wg. płci , ocen lub należy samodzielnie zadecydować na ile grup i na jakie grupy podzielić materiał statystyczny.

ZLICZANIE MATERIAŁÓW STATYSTYCZNYCH - informuje ile razy pojawia się dany wynik lub ile razy wynik trafia do danej grupy

ETAP IV

Opis statystyczny :

-Dotyczy tylko danej przebadanej zbiorowości statystycznej lub próby, niekoniecznie losowej

-Metody opisu wchodzą w zakres statystyki opisowej

Wnioskowanie statystyczne:

-Wnioskowane o całej zbiorowości statystycznej na pdst. Zbadania pewnej jej części zwanej próbą

-Jest możliwe wtedy tylko gdy próba jest reprezentatywna

-Metody wnioskowania statystycznego wchodzą w zakres statystyki matematycznej

RODZAJ BADANIA STATYSTYCZNEGO:

1.badania pełne (całkowite, kompletne ,wyczerpujące)- obejmuje wszystkie jednostki badanej zbiorowości,

2.badania częściowe (niecałkowite, niekompletne ,niewyczerpujące, niepełne)- obejmuje tylko niektóre jednostki zbiorowości statystycznej,

3.szacunki interpretacyjne i ekstrapolacyjne

RODZAJE BADANIA PEŁNEGO:

1.spis statystyczny- jest okresowym lub doraźnym badaniem statystycznym obejmującym wszystkie jednostki zbiorowości statystycznej np. spis powszechny

2. rejestracja bieżąca- jest systematycznym notowaniem pewnych …

RODZJE BADAŃ CZĘŚCIOWYCH:

1.Badania ankietowe- inf. O zbiorowości są gromadzone za pomocą ankiety kierowanej do ściśle określonych osób,

2.Badania monograficzne- szczegółowy opis i analiza wybranej jednostki typowy powszechnie występującej, reprezentatywnej dla interesującego nas procesu lub zjawiska. Opis z punktu widzenia ustalonych parametrów istotny dla analizowanego procesu,

3.Badania reprezentacyjne - częściowe badanie oparte na

INTERPRETACJA- szacowanie nieznanych wartości cechy na podst. znanych wartości sąsiednich wcześniejszych i późniejszych.

EKSTRAPOLACJA- szacowanie nieznanych wartości celem wykraczającym poza przedział wartości znanych

-Mogą mieć charakter liniowy i nieliniowy

-W przypadku liniowym opierają się na założeniu że rozkład wartości klasy jest proporcjonalny do liczebności,

Etapy opracowania danych z badania statystycznego.

1) Przygotowanie badania.

-Cel badania

-Przedmiot badania w ujęciu rzeczowym, czasowym i terytorialnym

-Zakres badania- wybór cech charakterystycznych podlegających badaniom

-Metoda badania (pełne lub częściowe)

-Plan badań, czyli harmonogram, formularze, instrukcje statystyczne

Formularze statystyczne jest to zbiór spisanych pytań dotyczących badanych cech rozważanych zbiorowości statystycznych.

2)Materiał statystyczny jest to zbiór informacji o wartościach badanych cech w poszczególnych jednostkach statystycznych, który powstaje w wyniku prowadzonych obserwacji

Dzielimy go na

-Pierwotny materiał zebrany specjalnie dla naszych celów

-Wtórny obejmuje materiały już poprzednio zebrane przez inne jednostki i wykorzystane dla naszych celów, np. GUS

Kontrola materiału statystycznego

-Kontrola formalna, czyli kompletność zebranego materiału,

-Kontrola merytoryczna- obejmująca kontrole zgodności rachunkowej i logicznej poprawności zapisów

3) Przygotowanie materiału statystycznego do opracowania. Stosujemy dwa etapy opracowania materiału statystycznego:

1. Grupowanie - polega na podziale całej zbiorowości statystycznej na mniejsze części

-Grupy proste - jedna cecha statystyczna

-Grupy złożone - co najmniej dwie cechy statystyczne

Po podzieleniu zbiorowości na grupy według pewnej cechy ustalamy kolejność oraz nazwy tych grup otrzymujemy uporządkowane nazwy grup tworzące wykaz klasyfikacyjny.

4) Opracowanie materiału statystycznego

Metody techniczno-organizacyjne opracowania materiału statystycznego. Po dokonaniu grupowania statystycznego następuje zliczenie materiału, czyli ustalenie liczebności poszczególnych grup. Rozróżniamy np. sposoby zliczenia materiałów:

-Bezpośrednie - ręczne

-Sposób kreskowy,

-Sposób kartkowy,

5) Prezentacja danych statystycznych.

Rozróżniamy trzy sposoby prezentacji:

-Metoda tabelaryczna,

-Metoda graficzna,

-Metoda opisowa.

6) Analiza struktury

Struktura zbiorowości określona jest przez podział badanej zbiorowości statystycznej na grupy jednostek różniących się od siebie wartościami poszczególnych cech. Liczbową formą opisu struktury są liczby względne powszechnie stosowane jako wskaźnik struktury.

Metody prezentacji opracowanego materiału statystycznego.najprostszą formą jest szereg statystyczny, złożoną formą jest tablica statystyczna (wykorzystujemy w niej szeregi co najmniej dwa) , wykres jest bardzo komunikatywny, ale jest mało dokładny.Należy korzystać z ogólnie uznanych i powszechnie stosowanych pojęć, definicji, jednostek miary, kryteriów klasyfikacji, symboli umownych. Wykres statystyczny jest uzupełnieniem dla tablicy, jest wtórna formą prezentacji. Rodzaje wykresów : liniowe, powierzchniowe, pasmowe, punktowe, bryłowe, mapowe, obrazkowe, kombinowane, specjalne. Szeregi statystyczne - zbiór wyników obserwacji jednostek według pewnej cechy .Rodzaje szeregów statystycznych:-szczegółowe - prezentują materiał uporządkowany wg wartości cechy-rozdzielcze - prezentują materiał uporządkowany wg wariantów badanej cechy (mierzalnej lub niemierzalnej) przy czym poszczególnym wariantom przyporządkowane są ich liczebności, określają strukturę badanej zbiorowości1)punktowe 2)przedziałowe-przestrzenne - przedstawiają rozmieszczenie wielkości statystycznych wg jednostek administracyjnych, części świata-dynamiczne - prezentują z kolei rozwój zjawisk w czasie przy czym może tu być uwzględniony ściśle uwzględniony moment np.: 31,12 danego roku12.) Sposoby graficznej prezentacji opracowanego materiału statystycznego .Graficzna prezentacja danych:Wykresy słupkowe.Wykresy kołowe.Wykresy obrazkowe(piktogramy).Diagramy szeregów czasowych.Histogram.Wykresy częstości.Wykresy częstości i procentów skumulowanych.WYKRES-jest to graficzna forma rejestracji danych oraz narzędziem prezentacji i analizy uogólnionych informacji statystycznych. Najczęściej Wykresy sporządza się na podstawie tablic statycznych, ale nie mogą być one prostym powtórzeniem zawartych w nich danych. Wykres ujmuje zjawiska w sposób bardziej syntetyczny niż tablica. Każdy wykres podobnie jak tablica powinien mieć tytuł i źródło danych na podstawie, których należy podać legendę, czyli wyjaśnienie zastosowanych symboli.
W grafice statystycznej wyróżnia się następujące rodzaje wykresów:
-liniowe; powierzchniowe; pasmowe; bryłowe(np. kołowe słupkowe); punktów; wagowe; kombinowane i specjalne. Częstości absolutne ni liczba rzeczywista obserwacji odpowiadających danej wartości cechy lub jej przedziale klasowemu częstość względna ni/n ( n to liczba elementów przed) iloraz częstości absolutnej każdej wartości cechy lub jej przedziału klasowego przez ogólną liczbę obserwacji częstość skumulowana jest sumą częstości wszystkich poprzednich wartości lub przedziałów do danej wartości lub przedziału włącznie Dystrybuanta - funkcja rzeczywista jednoznacznie wyznaczająca rozkład prawdopodobieństwa (tj. miarę probabilistyczną określoną na ciele borelowskich podzbiorów prostej, a więc zawierająca wszystkie informacje o tym rozkładzie. Dystrybuanty są efektywnym narzędziem badania prawdopodobieństwa ponieważ, są obiektem prostszym niż rozkłady prawdopodobieństwa. Dystrybuanta rozkładu próby zwana jest dystrybuantą empiryczną. Jest ona blisko związana z pojęciem rangi.
Rodzaje miar statystycznych1) miary położenia: a) średnie : arytmetyczna, geometryczna, harmoniczna, potęgowa b) mediana (wartość środkowa) c) kwartale (wartości ćwiartkowe) d) dominanta (moda - wartość typowa)2) miary zmienności a) obszary zmienności b) wariancje i odchylenie standardowe c) odchylenie przeciętne d) odchylenie ćwiartkowe e) współczynnik zmienności f) momenty 3) miary asymetrii (skośności rozkładu empirycznego) 4) miary koncentracji a) jako mierniki nierównomierności rozłożenia wartości badanej cechy pomiędzy poszczególne przedziały klasowe b) jako mierniki skupienia jednostek wokół Srednia arytmetyczna jest to iloraz sumy n liczb i n (gdzie n to ilość sumowanych liczb). Stosuje się ją do szeregu rozdzielczego punktowego. Średnią arytmetyczną ważoną można interpretować jako współrzędną środka masy układu punktów materialnych o masach ni, umieszczonego na osi liczbowej w punktach 16.) co to są Miary tendencji centralnej? Wymienić najczęściej stosowane miary tendencji centralnej i podać sposoby ich obliczania dla różnych sposobów podawania danych statystycznych. Tendencja centralna w zbiorowości, to wskazanie wartości badanej cechy w zbiorowości statystycznej, wokół której skupione są wartości cech wszystkich jednostek wchodzących w skład tej zbiorowości. Tendencję centralną można określić wykorzystując miary tendencji centralnej (inaczej miary przeciętne lub średnie). Obliczanie tych miar pozwala na ścisłe scharakteryzowanie poziomu jakiegoś zjawiska występującego w zbiorowości statystycznej, używając tylko jednej lub kilku liczb.Przykładowymi miarami tendencji centralnej są:-średnia arytmetyczna·średnia geometryczna·średnia harmoniczna·średnia kwadratowa·mediana·moda Szereg szczegółowy prezentuje materiał uporządkowany wg wartości cechy Szeregi rozdzielcze prezentują materiał uporządkowany wg wariantów badanej cechy przy czym poszczególnym wariantom przyporządkowane są ich liczebności , określają strukturę badanej zbiorowości . Szeregi dzielimy na punktowe( dla cechy skokowej przyjmującej ze zbioru stosunkowo mało licznego ) oraz szeregi przedziałowe dla zbiorów liczebnych. Zasady budowy szeregów rozdzielczych. Przy dużej liczebności próby wartość próby grupuje się w klasach - przedziałach najczęściej jednakowej długości przyjmując ze wszystkie wartości w danej klasie są identyczne ze środkiem klasy. Żadna klasa nie może być pusta. Żadna wartość nie może znaleźć się poza szeregiem. Granice dokładności klas ustala się z dokładnością do ½ alfa gdzie alfa oznacza dokładność z jaka wyznaczono wartości w próbie. Szeregi rozdzielcze punktowe buduje się dla cechy skokowej np.: ocena z egzaminu , liczba dzieci w rodzinie.Budując szeregi rozdzielcze musimy na samym początku zdecydować o liczbie przedziałów klasowych na rzecz rozpiętości i sposobie określania granic przedziałów. Szereg rozdzielczy przedziałowy buduje się dla cechy ciągłej gdzie wartości tej cechy grupujemy w określonych przedziałach. Liczba Przedziałów(klas)w szeregu uzależniona jest od obszaru zmienności badanej cechy to jest różnicy między maximum i minimum wartości cechy o liczebności zbiorowej oraz od celu badania .Im większy obszar zmienności i liczebności zbiorowej tym więcej powinno być przedziałów.Rozpiętość przedziału zwana interwałem jest różnica między górną i dolną granicą klasy .Jest ona uwarunkowana obszarem zmienności badanej cechy a tym samym liczbą ustalonych klas. Wartość środkowa(mediana) jest miarą tendencji centralnej, w uporządkowanej z punktu widzenia badanej cechy zbiorowości jest tą wartością, która jest dokładnie po środku , ma sens w przypadku uporządkowanych danych liczbowych lub skal porządkowych pozwalających Dominanta (wartość modalna, moda, wartość najczęstsza)- wartość cechy która w danej wartości występuje najczęściej. W szeregach rozdzielczych punktowych dominanta jest tą wartością cechy która odpowiada największej liczebności ale nie może być to wartość najmniejsza ani największa ( wtedy nie ma mody ) Obliczanie dominanty: dla szeregów rozdzielczych przedziałowych - wyznaczamy najliczniejszy przedział , przedział w którym znajduje się dominanta, wartość dominanty wyznaczamy ze wzoru : D= xd( dolna granica przedziału w którym znajduje się dominanta) + [ (liczebność przedziału - liczebność przedziału poprzedzającego dominantę) / ( liczebność przedziału -liczebność przedziału poprzedzającego dominantę)+ (liczebność przedziału -liczebność przedziału następującego po dominancie ] * długość przedziału czyli h Miary dyspersji (zróżnicowania, zmienności) Wymienić bezwzględne i względne miary dyspersji.
Są to miary które dają pełną informację o strukturze zbiorowości, charakteryzują wewnętrzne zróżnicowanie elementów w zbiorowości statystycznej.
Miary bezwzględne: obszar zmienności, wariancja, odchylenie standardowe, odchylenie przeciętne, odchylenie ćwiartkowe.
Miara względna: współczynnik zmienności..
Wariancja- miara która mierzy stopień rozproszenia wartości cechy wokół wartości przeciętnej (średniej)
Odchylenie przeciętne - średnia arytmetyczna bezwzględnych różnic pomiędzy wartościami cachy a jej średnim poziomem (wartości średnią).
Rodzaje obszarów zmienności.
- typowy klasyczny obszar zmienności
x śr - σ < x < x śr + σ
- typowy pozycyjny obszar zmienności
Me - Q < x < Me + Q
Współczynniki zmienności.
- stosunek odchylenia standardowego do wartości średniej
* dla zbiorowości
Vσ = σ/m * 100 %
* dla próby
Vs = s/ x śr * 100%
- stosunek odchylenia przeciętnego do wartości średniej
* dla zbiorowości Vdm = dm/m * 100%
* dla próby
Vx śr = dx śr/ x śr * 100%
- stosunek odchylenia ćwiartkowego do mediany
V_Q = Q/ Me * 100%
Co to jest asymetria szeregu statystycznego. Podać graficzną interpretacje szeregu lewostronnie i prawostronnie asymetrycznego. Wymienić i scharakteryzować miary skośności.
Rozkład empiryczny jest asymetryczny jeżeli wartość cechy która przybiera największa fakcja (dominata) odbiega od wartości średniej.
- rozkład lewostronnie asymetryczny
- rozkład prawostronnie asymetryczny
Miary skośności:
- współczynnik skośności
* dla zbiorowości
As = (m - Dm) / σ
* dla próby
As = (x śr - Dx śr) / s
- klasyczny współczynnik asymetrii
* dla zbiorowości
g = µ₃ / σ³
* dla próby
g = µ₃ / s³
- pozycyjny współczynnik asymetrii
A_Q = (Q₃ + Q₁ - 2Me) / Q₃-Q
Co to jest koncentracja? Wymienić i scharakteryzować współczynniki koncentracji. Omówić sposób wyznaczania koncentracji Lorentza.
Koncentracja - jest to nierównomierne rozdysponowanie łącznej sumy wartości cechy w badanej zbiorowości pomiędzy poszczególne jednostki tej zbiorowości.
Współczynniki koncentracji:
- kurtoza- mierzy stopień koncentracji wartości wokół wartości średniej
* dla zbiorowości
Kσ = µ₄ / σ⁴
* dla próby
Ks = µ₄ / s⁴
- eksces- miara spłaszczenia dla rozkładów jednorodnych, porównuje dany rozkład z rozkładem normalnym dla którego K=3
E = Ks - 3
- współczynnik koncentracji Lorentza
KL= 1 - (b / 5000)
b ={ wi*(F_zi + F_zi-1)}/2
wi = ni/n * 100%
zi ={ xi * ni / ∑( xi * ni)} * 100%.
Szereg czasowy - ciąg obserwacji pewnego zjawiska albo cechy w kolejnych jednostkach czasu
Sposób prezentacji: w formie zbioru, tabeli lub graficznie - elementy szeregu czasowego są reprezentowane przez punkty płaszczyzny o współrzędnych( t , yt), które łączy się z reguły odcinkami linii prostej.
Niech (t=1,2,..n) oznacza przedziały czasowe w których obserwowano wartości pewnej zmiennej.
yt - wynik obserwacji
Szereg czasowy możemy zapisać jako zbiór {yt: t=1,2,…n}
Czynniki, które najczęściej wpływają na rozwój zjawiska w czasie.
- trend - długotrwałe, systematyczne zmiany, jakim podlega dane zjawisko.
- wahania sezonowe - regularne, o określonym cyklu ( np. rocznym,kwartalnym, miesięcznym, tygodniowym lub związanym z porą dnia)
- wahania cykliczne - systemowe, falowe wahania rozwoju gospodarki związane z cyklem koninkturalnym obserwowane w okresach dłuższych niż roczne.
- wahania przypadkowe - wszystkie nieregularne zmiany.
Szereg czasowy bez trendu - szereg czasowy z eliminowanymi czynnikami ( trendem, wahaniami sezenowymi, cyklicznymi i przypadkowymi) które nie mają wpływu na dane zjawisko.
Sposoby wygładzania takiego szeregu:
- średnia arytmetyczna
- średnia ruchoma
- metoda wyrównywania wykładniczego Browna. Średnia ruchoma-srednia liczona dla mniejszej ilości elementow szeregu czasowego.Średnie ruchome można obliczyc z : -sr ruchome scentrowane-parzystej liczby kolejnych wyrazow szeregu-sr ruchome zwykle-nieparzystej liczby kolejnych wyrazow szeregu przykład-srednie ruchome zwykle, Szereg czasowy z trendem szereg w którym obserwujemy powolne regularne i systematyczne zmiany oraz towarzysza temu przypadkowe (losowe) zmiany.Sposób wyznaczania funkcji: ogona zasada dopasowujemy typ funkcji matematycznej do całego szeregu czasowego.Kolejność postępowania:1. wybieramy odpowiedni typ funkcji trendu ( dokonujemy tego na podstawie wykresu szeregu czasowego)2. szacujemy parametry wybranej funkcji.Przy wyborze typu funkcji kierujemy się zasada: rodzaj funkcji możliwie najprostszy, parametry funkcji maja merytoryczne znaczenie w opisie rozwoju badanego zjawiska Wahania sezonowe w szeregu czasowym-regularne o określonym cyklu (np. rocznym, miesięcznym, tygodniowym lub związanym z pora dnia) odchylenia od tendencji rozwojowej (trendu)dekompozycja szeregu- wyodrębniamy poszczegolne wyniki wpływające na zmienność rozwazanego zjawiska w czasieDekompozycja dla szeregu multiplikatywnego:Rozwazmy model multiplikatywny, w którym trend (T₁), wahania sezonowe (S_t), wahania cykliczne (C_y) i wahania przypadkowe ( I_t) determinuja badane zjawisko poprzeez przemnożenie wszystkich czynnikow Y_t=T_t*S_t*C_t*I_t Prognozowanie Metody prognozowania: metoda średniej arytmetycznej, średniej ruchomej, oparta na ważonej średniej ruchomej, oparta na wygladzaniu wykladniczymśredni błąd kwadratowy ex post
MSE = (y_t-S_t)²\n Przyrost absolutny-roznica zaobserwowana w poziomie danego zjawiska w dwóch rożnych okresach( momentach) czasowych . ∆y_t=y_t-y_t* y_{t- poziom tego} samego zjawiska w okresie obserwowanym badanym y_t* -poziom zjawiska w okresie przyjętym za podstawe porównań. Rodzaje: -przyrosty absolutne jednopodstawowe-przyr ze stala podstawa porównań, wlk zj w kolejnych okresach jest porównywana ze stała wielkością z okresu bazowego, najczęściej okresem bazowym jest okres wyjscjiowy,y₀- wielkość zjawiska w okresie bazowym przyrosty absolutne łańcuchowe-przyrosty o zmiennej podstawie porównań, za okres bazowy przyjmujemy okres poprzedzający okres badany, okres badany w pierwszym etapie służy za bazowy w kolejnym porównaniu, tworząc ciąg łańcuchowych przyrostów y₂-y₁, y₃-y₂,…., y_n-y _n-1 lub ∆y_t=y_t-y_t-1 t=2,3,…n Przyrost względny jest to stosunek przyrostu absolutnego do poziomu zjawiska w okresie podstawowym, pozwala porównywać dynamike 2 roznych zjawisk. Wyróżniamy 2 rodzaje: --przyrosty względne jednopodstawowe -stosunek przyrostu absolutnego jednopodstawowegodo poziomu zjawiska w okresie pryjetym za podstawe ∆y_t\y₀=(y_t-y₀)\y₀ -przyr względne łańcuchowe-stosunek przyrostu absolutnego łańcuchowego do poziomu zjawiska w okresie t=1, bezpośrednio poprzedzającym okres t (y_t-y_t-1)\y_t- Indeksy statystycne- miary względne służące do analizy zmian zjawiska w czasie, znajduje zastosowanie w porównywaniu dynamiki zjawisk również takich , które wyrazone sa w innych jednostkach.. metody indeksowe: indeksy indywidualne(jednopodstawowe,łańcuchowe), indeksy agregatowe Indeksem indywidualnym nazywamy wielkości tego samego zjawiska w dwóch rożnych okresach dla zjawisk jednorodnych w czasie np. produkcji tego samego wyrobu. W przypadku porównywania zjawisk niejednorodnych niejednorodnych czasie konieczne jest wyrażenie wielkości badnego zjawiska wartościowo. Indeks agregatowy jest to indeks zespołowy, sluzy do badania zjawisk o zróżnicowanej strukturze. Aby stworzyć indeks agregatowy należy doprowadzić do sumowalnosci pewne rożne produkty,często wyrażone w rożnych jednostkach, tworząc agregat(zbiór różnych produktow składających sie na zjawisko, którego dynamike zamierzamy badac) badamy wartość spożycia w dwóch różnych okresach: badanym (n) i podstawowym (0) możemy ustalic zmiany w poziomie zjawisk obliczając indeksy:wartości ilości i cen. Stosunek wielkości zjawiska w okresie t (badanym) do wielkości tego zjawiska w okresie podstawowym(badanym) i_yt\0=y_t\y₀ i_yt\0=y_t\y₀*100% y_t-wielkosc zjawiska ilość lub wartość w okresie t y₀-wielkosc zjawiska w okresie 0(y₀ nierowna się 0) indeksy jednopodstawowe- Jeżeli: i_yt\0>1 zj wzrosło w okresie t w porównaniu z okresem 0 i_yt\0<1 zj spadlo w okresie t w porównaniu z okresem 0 i_yt\0=1 zj w okresie t w stosunku do okresu 0 nie uleglo zmianie. zastosowanie indeksu jednopods: wykorzystywane do porównywania wielkości badanego zjawiska w jednym lub kilku okresach z jego wielkością w dowolnym przyjętym za podstawe okresie, okres podstawowy nie może być okresem nietypowym indeksy indywidualne łańcuchowe Sluza do badnia tempa zmian, indeksy lancucowe jest to stosunek wielkości zjawiska w okresie badanym t do wielkości zjawiska w okresie t-1 bezposrednio poprzedzającym i_yt\t-1=y_t\y _t-1 i_yt\t-1=y_t\y _t-1 *100% -Ind lancuchowe przedstawione w szeregu czasowym informują o tym jak zmieniło sie badane zjawisko z okresu na okres -jeżeli kolejne i_yt\t-1>1 to zjawisko charakteryzuje sie tempem rosnącym -jeżeli kolejne i_yt\t-1<1 to zj charakteryzuje się tempem malejącym Srednie tempo zmian zjawiska jest wyznaczane przez srednia geometryczna y_g=pierwiastek stopnia n-1√y_n\y₁ Rachunek indeksów indywidualnych a) zmiana indeksów łańcuchowych na jedno podstawowe iyn/k=yn/yk=yn/yn-1 x y n-1/y n-1 x… x yk+2/yk+1 x y k+1/yk = i y_n/_n-1 x i y _n-1/n-2 x … x i y _k+2/k+1 x i y _k+1/k Zamiany indeksów łańcuchowych na jednopodstawowe dokonujemy według następujących zasad:
1. Indeks jednopodstawowy w okresie następującym bezpośrednio po okresie przyjętym za podstawę jest taki sam jak indeks łańcuchowy.
2. Indeks jednopodstawowy w okresie przyjętym za podstawę wynosi 100%.
3. Dalsze indeksy jednopodstawowe po okresie przyjętym za podstawę otrzymujemy mnożąc w sposób narastający (kumulując) kolejne indeksy łańcuchowe, licząc od wskaźnika łańcuchowego znajdującego się tuż po okresie podstawowym.
4. Indeksy jednopodstawowe przed okresem podstawowym są odwrotnością narastających iloczynów kolejnych indeksów łańcuchowych, licząc od okresu przyjętego za podstawę.
Zmiany podstawy w indeksach jednopodstawowych dokonujemy przez dzielenie poszczególnych indeksów przy danej podstawie przez indeks jednopodstawowy tego okresu, który przyjmujemy za nową podstawę. b)Zmiana podstawy w indeksach jednopodstawowych i y n/a= Y_n/Y_a = Y_n/Y_b//Y_a/Y_b= i Y _n/_b// i Y_a/_b c)zmiana indeksów jednopodstawowyh na łańcuchowe i Y_n / n-1= Y_n/ Y _n-1 =Y_n / Y_a // Y_n-1 / Y_a = i Yn/a //i Y n-1/a AGREGAT- zbiór różnych produktów składających się na zjawisko, którego dynamikę zamierzamy badać. Jak wyznaczać: *należy doprowadzić do sumowalności pewne różne produkty, często wyrażane w różnych jednostkach.*tworząc agregaty badamy wartości spożycia w dwóch różnych okresach: badanym(n) i podstawowym (o), możemy ustalić zmiany w poziomie zjawiska obliczając indeksy: wartości, ilości, cen. Agregatowy indeks wartości Dla całej zbiorowości rozumiany jako:-spożycie wszystkich towarów-produkcja wszystkich towarów-produkcja wszystkich usług I_w=W _n/o = ∑Wjn/∑Wjo= ∑ q j_n p j_n/∑ qj_opj_o licznik jest łączną wartością produkcji w okresie badanym (n) mianownik jest całkowitą wartością produkcji w okresie podstawowym (o) *Informuje o łącznych zmianach wartości towarów wszystkich produktów tworzących agregat w okresie badanym w stosunku do okresu podstawowego-Jeżeli Iw>1 to tendencja jest wzrostowa -jeżeli Iw<1 tendencja spadkowa -Iw=1, to brak zmian Agregatowy indeks ilości-Zmiany cen w dłuższych okresach czasu nie wynikające z przyczyn niezależnych maja wpływ na wartości indeksu ilości i mogą wpływać na końcowy wynik badania opartego na indeksach wartości w sposób zmieniający rzeczywista sytuacje.*To jest indeks określający wpływ zmian ilości na dynamikę wartości prze cenach na pozornie stałym poziomieAgregatowy indeks ilości: wg. Formuly Lespeyresa (podstawowy),wg formuly Paaschego(badany)Agregatowy indeks ilości: wg. Formuly Lespeyresa L Iq=LQ _n/o= ∑_j=1 ^k q j n x pjo/ ∑ _j=1 ^k qjo x pjo Gdzie: -licznik-łączna wartość produkcji(spożycia) w okresie badanym -mianownik- łączna wartość produkcji9spozycia) w okresie podstawowym*został obliczony przy założeniu, ze ceny badanych agregatów nie zmieniły się*indeks ten informuje o dynamice ilości produktów wchodzących w skład badanego agregatu Agregatowy indeks ilości wg formuly Paaschego pIq = pQ _n/o = ∑ _j=1 ^k Ajn x pjn//∑ _j=1 ^k qjo x pjn *licznik - łączna wartość produkcji w okresie badanym w cenach okresu badanego *mianownik łączna wartość produkcji w okresie podstawowym w cenach okresu badanego *informuje o jaki procent wzrosła lub zmalała średnia ilość badanego agregatu

45. Agregatowy indeks cen według formuły Laspeyresa

gdzie:

p_i0 - cena i-tego artykułu w okresie podstawowym

p_it - cena i-tego artykułu w okresie badanym

q_i0 - ilość sprzedaży lub zakupu i-tego artykułu w okresie podstawowym

W_i0 - wartość sprzedaży lub zakupu i-tego artykułu w okresie podstawowym

- indeks zmiany ceny i-tego artykułu

mówi nam o ile procent zmieniła się łączna wartość sprzedaży w okresie badanym w porównaniu do okresu podstawowego w wyniku zmian cen sprzedanych artykułów (pod warunkiem, że ilości sprzedanych artykułów w okresie badanym są równe ilościom artykułów sprzedanych w okresie podstawowym).

-
mówi nam o ile procent przeciętnie zmieniły się ceny sprzedanych artykułów w okresie badanym w porównaniu do okresu podstawowego (pod warunkiem, że ilości sprzedanych artykułów w okresie badanym są równe ilościom artykułów sprzedanych w okresie podstawowym)

Wielkości stosunkowe

Wielkości stosunkowe są wskaźnikami natężenia wyrażającymi stosunek dwóch zjawisk logicznie ze sobą powiązanych.

Przykładem wielkości stosunkowych mogą być takie kategorie jak:

- wydajność pracy (iloraz produkcji i czasu pracy);

- koszt jednostkowy (iloraz nakładów i wielkości produkcji);

- średnia płaca (iloraz funduszu płac i zatrudnienia);

- płodność (iloraz urodzeń żywych i ogólnej liczby kobiet w wieku rozrodczym);

- umieralność (iloraz liczby zgonów i ogólnej liczby ludności).

Każdą wielkość stosunkową można rozpatrywać jako ogólną (zespołową) i cząstkową (jednostkową). Na przykład stosunek liczby urodzeń żywych w okresie t do liczby kobiet w wieku rozrodczym (15 - 49 lat) jest wielkością ogólną. Natomiast stosunek liczby urodzeń żywych w grupie kobiet w wieku 25 - 29 lat do ogólnej liczby kobiet w tym wieku jest wielkością stosunkową cząstkową.

INDEKS WSZECHSTRONNY

Pierwszy sposób obliczania wymaga znajomości poziomów czynnika a i b dla każdej cząstki zbiorowości i to w obydwu okresach (podstawowym i badanym).
Drugi sposób wymaga informacji o cząstkowych o wielkości stosunkowej x i czynnika b - jest to iloraz dwu średnich arytmetycznych ważonych (wagą jest czynnik b).
Jeżeli posiadamy informację o cząstkowych wielkościach stosunkowych oraz o czynniku a to możemy skorzystać ze sposobu trzeciego - iloraz dwu średnich harmonicznych ważonych (wagą jest czynnik a).

Wartość indeksu wszechstronnego jest wypadkową działania dwóch czynników, a mianowicie:
1. dynamiki cząstkowych wielkości stosunkowych;
2. zmian w strukturze czynnika a lub b.
Wpływ na dynamiki cząstkowych wielkości stosunkowych na poziom indeksu wszechstronnego określają indeksy zespołowe wielkości stosunkowych o stałej strukturze. Wskaźniki dynamiki (indeksy)

Indeksem (wskaźnikiem dynamiki) nazywamy każdą liczbę względną powstałą przez podzielenie wielkości danego zjawiska w okresie badanym (sprawozdawczym) przez wielkość tego zjawiska w okresie podstawowym (bazowym).

Jeżeli poziom zjawiska w okresie (momencie) badanym oznaczamy symbolem y1, a w okresie (momencie) podstawowym symbolem y0 to wzór na indeks przyjmuje postać:

Indeks jest wielkością niemianowaną i może być wyrażony w ułamkach lub w procentach.

Jeżeli indeks przyjmuje wartość z przedziału 0 < i < 1, to świadczy to o spadku poziomu zjawiska w badanym okresie w stosunku do okresu podstawowego. Wartość większa od 1 (lub 100%) świadczy o wzroście poziomu zjawiska w okresie badanym w stosunku do okresu podstawowego. Wartość indeksu równa 1 świadczy o tym, że poziom zjawiska w okresach badanym i podstawowym są takie same.

W zależności od przyjętej podstawy wyróżniamy indeksy jednopodstawowe lub łańcuchowe.

Tablica korelacyjna jest to wynik próby przedstawiony jako punkty na płaszczyźnie. Tablicę korelacyjną (tablicę dwudzielną) buduje się zazwyczaj dla próby o liczebności n>30. Zasady budowy:- budujemy szereg rozdzielczy dla każdej cechy oddzielnie (dla cech X i Y)-patrzymy ile jest takich punktów, które pasują np. do n11 itp. Nij- liczebność tych (xi, yi) dla których xi należy do i-tej klasy zmiennej X, a yi należy do j-klasy dla zmiennej Y. Analiza korelacyjna polega na badaniu siły zależności liniowej między dwiema cechami mierzalnymi tzn. miedzy zmiennymi losowymi X i Y.

Załóżmy ze dla zmiennej losowej X, Y istnieją niezerowe wariancje D²X i D²Y. Dysponujemy wynikami n- elementowej próby: (x_1,y₁), (x₂,y₂), ..., (x_ny_n), które traktujemy jako wartości zmiennych losowych (X₁,Y₁), (X₂,Y₂), ..., (X_n,Y_n). Wyniki próby możemy traktować jako punkty na płaszczyźnie, otrzymując w ten sposób diagram korelacyjny. Ma on sens dla dużej ilości danych, dla próby o liczności n>30 buduje się zazwyczaj tzw. tablicę korelacyjną. Miary zależności korelacyjnej między zmiennymi. -współczynnik zbieżności Czuprowa;
-wskaźniki (stosunki) korelacyjne Pearsona; -współczynnik korelacji liniowej Pearsona; -współczynnik rang (korelacji kolejnościowej) Spearmana Zależność funkcyjna- występuje bardzo rzadko, dwie zmienne pozostają w związku funkcyjnym jeśli zmiana wartości jednej z nich powoduje ściśle określoną zmianę wartości drugiej. y=ax+b, x- ilość pracy wykonanej w systemie akordowym, a- cena za jednostkę, b- pewien poziom płacy stałej, y- płaca w akordzie y=x^2, x- pewien odcinek, y- pole kwadratu (zależy tylko od długości odcinków). Zmiana x powoduje zmianę y. Zależność stochastyczna- występuje wtedy, gdy wraz ze zmianą wartości jednej zmiennej zmienia się rozkład prawdopodobieństwa drugiej zmiennej. Szczególnym przypadkiem zależności stochastycznej jest zależność korelacyjna (statystyczna). Polega ona na tym, że określonym wartościom jednej zmiennej odpowiadają ściśle określone średnie wartości drugiej zmiennej. Możemy zatem ustalić, jak zmieni się - średnio biorąc - wartość zmiennej zależnej Y w zależności od wartości zmiennej niezależnej X. Związki typu statystycznego są możliwe do wykrycia oraz ilościowego opisu w przypadku, kiedy mamy do czynienia z wieloma obserwacjami, opisującymi badane obiekty, zjawiska czy też procesy. Zależność korelacyjna Jest to szczególny przypadek zależności stochastycznej. Zależność korelacyjna polega ona na tym, że określonym wartościom jednej zmiennej odpowiadają ściśle określone średnie wartości drugiej zmiennej. Możemy zatem ustalić, jak zmieni się - średnio biorąc - wartość zmiennej zależnej Y w zależności od wartości zmiennej niezależnej X. Związki typu statystycznego są możliwe do wykrycia oraz ilościowego opisu w przypadku, kiedy mamy do czynienia z wieloma obserwacjami, opisującymi badane obiekty, zjawiska czy też procesy.

współczynnik korelacji liniowej Pearsona i podać jego interpretację.

Definiujemy go jako stosunek kowariancji do iloczynu odchyleń standardowych tych zmiennych.

Wartość współczynnika korelacji liniowej na podstawie n- elementowej próbki obliczamy według wzoru:
gdzie
- odpowiednie średnie:


Interpretacja wyniku 1.
,2.współczynnik korelacji jest miarą związku liniowego,
oznacza brak zależności liniowej, na tej podstawie nie można wnioskować o niezależności zmiennych,3.gdy
- korelacja dodatnia - wzrostowi wartości zmiennej X towarzyszy wzrost wartości zmiennej Y,4.gdy
- korelacja ujemna - wzrostowi wartości zmiennej X towarzyszy spadek wartości drugiej zmiennej,5.im
jest bliższy 1 tym zależność liniowa jest silniejsza, zwykle przyjmuje się: - < 0,2 - brak związku liniowego, - 0,2 - 0,4 - słaba zależność, - 0,4 -0,7 - umiarkowana zależność, - 0,7 - 0,9 - dość silna zależność, - > 0,9 - bardzo silna zależność. Własności współczynnika korelacji: 1. -1 £ rxy £ 1 2. znak współczynnika korelacji informuje o kierunku korelacji

(korelacja dodatnia -> wraz ze wzrostem jednej zmiennej rośnie. wartość drugiej zmiennej; korelacja ujemna - wraz ze wzrostem jednej zmiennej druga zmienna maleje) 3. warto__ bezwzględna informuje nas o sile związku: - rxy =0 - brak korelacji pomiędzy zmiennymi X i Y - rxy =1 lub rxy =-1 = wówczas miedzy zmiennymi zachodzi zależność w postaci funkcji liniowej

współczynnik korelacji rang Spearmana

Współczynnik korelacji rang Spearmana służy do opisu siły korelacji dwóch cech w przypadku gdy:

1.cechy są mierzalne, a badana zbiorowość jest nieliczna,

2.cechy mają charakter jakościowy i istnieje możliwość ich uporządkowania.

Współczynnik korelacji rang Spearmana stosuje się do analizy współzależności obiektów pod względem cechy dwuwymiarowej (X, Y). Zakładając, że badamy n obiektów opisanych za pomocą dwóch cech, należy te obiekty uporządkować ze względu na wartości każdej cechy oddzielnie (dla x_i - r_1i, a dla y_i - r_2i). Obiektom w każdym z uporządkowań przypisujemy liczbę określającą ich miejsce położenia (1,2,3,...,n). Numery te nazywa się rangami, a procedurę nadawania rang - rangowaniem. Wzór na współczynnik korelacji rang Spearmana jest następujący:

,

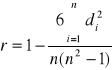
gdzie:

d_i = r_1i - r_2i,

r_1i - ranga i-tego obiektu w pierwszym uporządkowaniu,

r_2i - ranga i-tego obiektu w drugim uporządkowaniu,

n - liczba badanych obiektów.

Współczynnik korelacji rang Spearmana przyjmuje wartości z przedziału <-1,1>. Im bliższy jest on liczbie 1 lub -1, tym silniejsza jest analizowana zależność. Jego interpretacja jest analogiczna do interpretacji współczynnika Pearsona.

Liniowa funkcja regresji Metoda estymowania wartości oczekiwanej zmiennej y przy znanych wartościach innej zmiennej lub zmiennych x. Szukana zmienna y jest tradycyjnie nazywana zmienną objaśnianą, lub zależną. Inne zmienne x nazywa się zmiennymi objaśniającymi lub niezależnymi. Zarówno zmienne objaśniane, jak i objaśniające, mogą być wielkościami skalarnymi lub wektorami. Regresja w ogólności to problem estymacji warunkowej wartości oczekiwanej. Regresja liniowa jest nazywana liniową, gdyż zakładanym modelem zależności między zmiennymi zależnymi, a niezależnymi, jest funkcja liniowa.

---