Obliczenia wałków przekładni walcowej

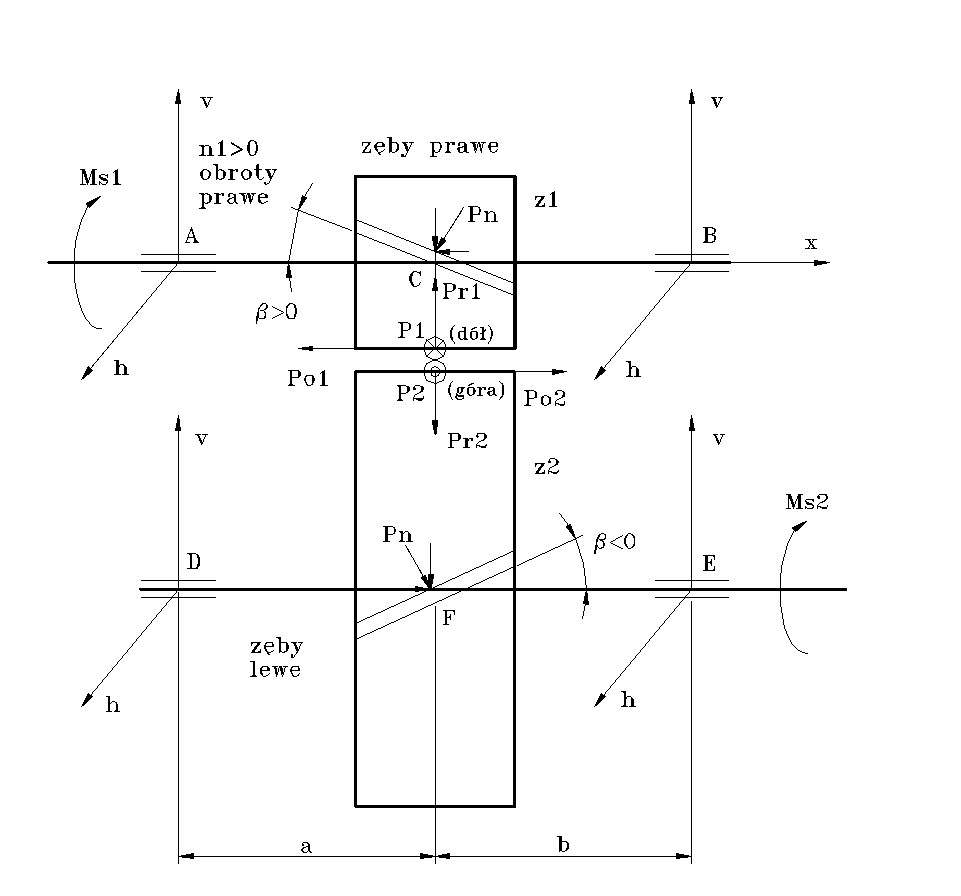
1. Wyznaczenie odległości między łożyskami i kołami zębatymi (wg rys.1)

Wałek nr1 i nr2

Odległość „a” między łożyskiem a środkiem koła walcowego z₂ (lub z₁) w funkcji

średnicy drugiego wałka

d₂ - przybliżona średnica wałka nr 2 z warunku na skręcanie

Szerokość łożyska „l_b”

l_b=0.6*d₂

Szerokość piasty „l_p” koła z₂

l_p=1.0*d₂

Luz między kołem a łożyskiem l_z =0.2*d_w2

Odległość „a” między lewym łożyskiem a środkiem koła z₂

a=0.5*l_b+0.5*l_p +l_z =0.3*d₂+0.5*d₂ +l_z=1.0*d₂

Odległość między środkiem koła zębatego a prawym łożyskiem też ma wynosić „a” (ze

względu na założoną symetrię położenia kół w korpusie).

2. Siły międzyzębne

Zwroty sił międzyzębnych będą zgodne ze zwrotami jak na rysunku nr 1,2 i 3 jeśli

iloczyn znaków pochylenia linii śrubowych zęba β_m i znaków obrotów n będzie dodatni,

czyli sign (β_m)*sign(n)>0 .

Wzory na składowe sił międzyzębnych

Siła obwodowa

,

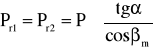
, (znak zależny od iloczynu sign (β_m)*sign(n))

gdzie d_m1 =d_t1 jest średnicą podziałową koła z₁ w przekroju czołowym.

Górne znaki w powyższych wzorach obowiązują, jeśli dodatni jest iloczyn znaków obrotów i kąta pochylenia linii zęba.

Dla koła z₂ zachodzą następujące zależności

,
,
.

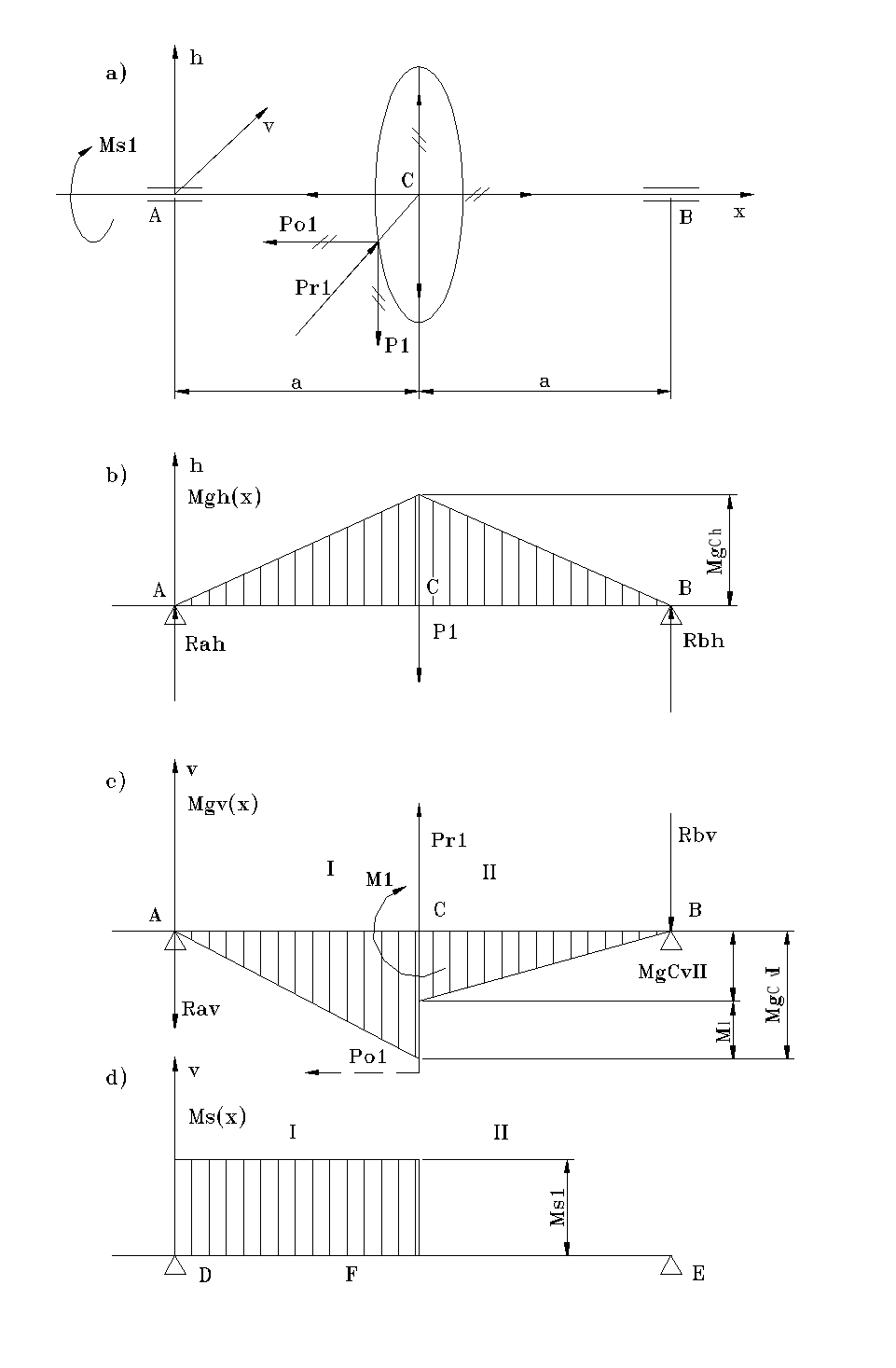
3. Obliczenia wałka nr 1

Układ sił i wykresy momentów przedstawiono na rys.2.

W płaszczyźnie h-x:

a. Obliczenia reakcji składowych na podporach R_Bh i R_Ah

Suma momentów względem punktu A

Σ M_iA= R_Bh*2*a-P₁*a= 0 , stąd obliczamy

składowe poziome „h” reakcji R_Bh i R_Ah w punktach B i A

R_Bh =P₁/2 ,

R_Ah=P₁-R_Bh =P₁/2.

b. Obliczenie momentów gnących w punktach A, B i C

Moment gnący w płaszczyźnie h-x w punktach A i B

M_gAh=0 , M_gBh=0 .

Moment gnący w punkcie C wynosi:

M_gCh=R_Ah*a.

W płaszczyźnie v-x:

Moment skupiony M₁ w punkcie C od siły osiowej P_o1

M₁=P_o1*d_m1/2

c. Obliczenia reakcji składowych na podporach R_Bv i R_Av

Suma momentów względem punktu A

Σ M_iA= -R_Bv*2*a-M₁+P_r1*a= 0 , stąd

wyznaczamy składową pionową „v” reakcji R_Bv w punkcie B

R_Bv=(P_r1*a-M₁)/(2*a)

Suma sił względem osi v

Σ P_iv= -R_Av-R_Bv+P_r1= 0, stąd

R_Av = P_r1-R_Bv

d. Obliczenie momentów gnących w punktach A, B i C

Moment gnący w płaszczyźnie v-x w punkcie C od lewej strony (I przedział)

M_gCvI= -R_Av*a ,

w punkcie C od prawej strony (II przedział)

M_gCvII= -R_Bv*a , a w punktach A i B

M_gAv=0, M_gBv=0.

d. Całkowite reakcje promieniowe (wypadkowe) na podporach

,

e. Całkowite momenty gnące (wypadkowe) w punktach A, B, C

dla k={A,B,C}, przy czym

,
,

M_gA= 0, M_gB= 0.

f. Obliczenie momentów zastępczych w punktach A, B, C

,

gdzie: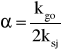
, M_s1= P₁*d_m1/2 .

Na granicach przedziałów momenty zredukowane wynoszą

, M_zB=0 .

,

W przypadku koła nacinanego przyjmujemy taki sam materiał wałka jak dla koła zębatego z₁ . W przeciwnym przypadku materiał wałka dobieramy z tablicy 16 skryptu do reduktora.

g. Średnicę wałka w dowolnym punkcie liczymy stosując hipotezę wytężeniową Hubera

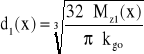
Dzielimy część wałka o długości „a” zaleca się podzielić na 3 lub 4 przedziały. W otrzymanych punktach obliczamy teoretyczną średnicę (lub promień wałka). Zarys wałka rzeczywistego powinien być ukształtowany na zewnątrz wałka teoretycznego, uwzględniając znormalizowane wartości średnic czopów pod łożyska toczne, uszczelnienia i wpusty.

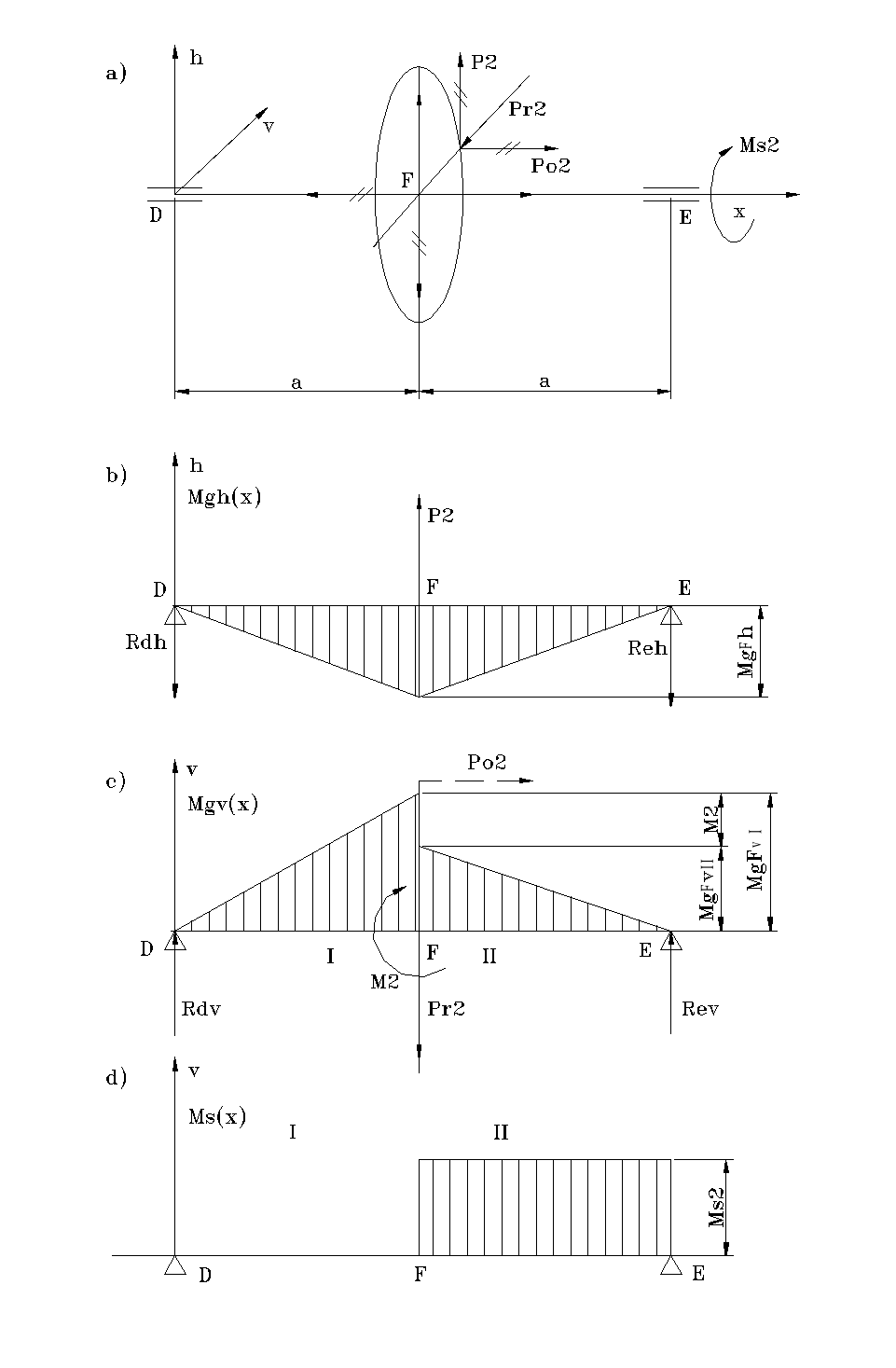
4. Obliczenia wałka nr 2

Układ sił i wykresy momentów przedstawiono na rys.3.

W płaszczyźnie h-x:

a. Obliczenia reakcji składowych na podporach R_Dh i R_Eh

Suma momentów względem punktu D

Σ M_iD= P₂*a-R_Eh*(2*a)= 0 , stąd obliczamy

składowe poziome „h” reakcji w punktach D i E

R_Eh =P₂/2 ,

R_Dh=P₂-R_Eh = P₂/2 .

b. Obliczenie momentów gnących w punktach D, E i F

Moment gnący w płaszczyźnie h-x w punkcie F

M_gFh=-R_Eh*a .

Moment gnący w punktach D i E wynosi:

M_gDh=0, M_gEh=0.

W płaszczyźnie v-x:

Moment skupiony M₂ w punkcie F od siły osiowej P_o2

M₂=P_o2*d_m2/2 ,

gdzie d_m2=d_t2 .

c. Obliczenia reakcji składowych na podporach R_Bv i R_Av

Suma momentów względem punktu D

Σ M_iD= -P_r2*a-M₂+R_Ev*(2*a)= 0 , stąd

wyznaczamy składową pionową „v” reakcji R_Ev w punkcie E

R_Ev=(P_r2*a+M₂)/(2*a)

Suma sił względem osi v

Σ P_iv= -P_r2+R_Ev+R_Dv = 0, stąd

R_Dv = P_r2-R_Ev

d. Obliczenie momentów gnących w punktach D, E i F

Moment gnący w płaszczyźnie v-x w punkcie F w „I” przedziale

(granica lewostronna)

M_gFvI= R_Dv*a,

a w przedziale II (granica prawostronna) moment gnący

M_gFvII= R_Ev*a, a w punktach D i E

M_gDv=0, M_gEv=0 .

d. Całkowite reakcje promieniowe (wypadkowe) na podporach

,

e. Całkowite momenty gnące (wypadkowe) w punktach D, E, F

dla k={D,E,F}, przy czym

,

M_gD=0, M_gE=0 .

f. Obliczenie momentów zastępczych w punktach D, E, F

,

gdzie: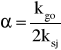
, M_s2= P₂*d_m2/2 .

Na granicach przedziałów momenty zredukowane wynoszą:

M_zD=0, M_zE=α*M_s2,

M_zFI= M_gFI,

Materiał wałka dobieramy z tablicy 16 skryptu do reduktora.

g. Średnicę wałka w dowolnym punkcie liczymy stosując hipotezę wytężeniową Hubera

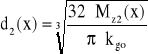
Dzielimy część wałka o długości „a” zaleca się podzielić na 3 (lub 4) przedziały. W otrzymanych punktach obliczamy teoretyczną średnicę (lub promień wałka). Zarys wałka rzeczywistego powinien być ukształtowany na zewnątrz wałka teoretycznego, uwzględniając znormalizowane wartości średnic czopów pod łożyska toczne, uszczelnienia i wpusty.

Rys.1

Rys.2

Rys.3

3

---